Точность и надежность оценки. Доверительный интервал. Доверительные интервалы для оценки математического ожидания и среднеквадратического отклонения нормального распределения.

Для выборок небольшого объема вопрос точности оценок решается с помощью интервальных оценок. При этом по вычисленной точечной оценке а* параметра а при заданной вероятности γ и а*, строят интервал для истинного параметра а: а*- ε<a<а*+ ε, чтобы выполнялось равенство: P(а*- ε<a<а*+ ε)=γ. Число ε называется точностью оценки а*, границы интервала а*- ε и а*+ ε называются доверительными границами, интервал (а*- ε;а*+ ε) – доверительным интервалом, вероятность γ – доверительной вероятностью или надежностью интервальной оценки.

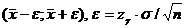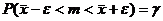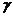Интервальной оценкой математического ожидания m нормального распределения при известной дисперсии σ² называется интервал , удовлетворяющий равенству: , где – заданная доверительная вероятность, m – истинное математического ожидание, 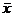– точечная оценка математического ожидания, n – объем выборки; число 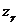находится из уравнения 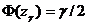с помощью табл.2 функции Лапласа Ф(х).

Следовательно, интервальная оценка математического ожидания находится по формуле: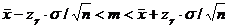

Интервальной оценкой математического ожидания m нормального распределения при неизвестной дисперсии называется интервал 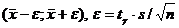, удовлетворяющий равенству: 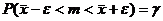где 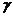– заданная доверительная вероятность, m – истинное математическое ожидание, 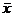– точечная оценка математического ожидания, s² – точечная оценка дисперсии, n – объем выборки, число 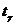вычисляется из уравнения 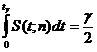с помощью таблицы распределения Стьюдента. Следовательно, интервальная оценка математического ожидания с доверительной вероятностью 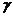вычисляется по формуле: .

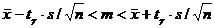Интервальной оценкой среднего квадратического отклонения σ нормального распределения называется интервал: 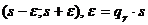удовлетворяющий равенству 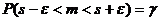где 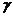– заданная доверительная вероятность, s² – исправленная выборочная дисперсия, n – объем выборки, число 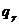определяется ил таблицы4.

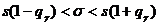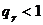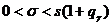Следовательно, интервальная оценка среднего квадратического отклонения находится по формулам: если , если .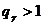

Статистическая проверка гипотез. Виды гипотез. Ошибки первого и второго рода. Статистические критерии проверки нулевой гипотезы. Критическая область. Проверка гипотез для нормального распределения. Корреляционная зависимость. Нахождение параметров уравнения линейной регрессии методом наименьших квадратов. Выборочный коэффициент корреляции, его свойства.

Статистической гипотезой называется предположение о виде распределения, о параметрах известных распределений. Например, стат.являются гипотезы: 1) генеральная сов-ть распределена по закону Пуассона( здесь сделано предложение о виде неизвестного распределения); 2) дисперсия двух нормальных сов-тей равны между собой (о параметрах двух известных гипотез)

Выдвинутая гипотеза называется нулевой (или основной) и обозначается Н_о.

Гипотеза, которая противоречит нулевой, называется конкурирующей гипотезой (или альтернативной гипотезой) и обозначается Н₁.

Гипотеза называется простой, если она содержит только одно предположение.

Гипотеза называется сложной, если она состоит из конечного или бесконечного числа предположений.

Ошибкой первого рода называется решение отвергнуть нулевую гипотезу H_o и принять конкурирующую гипотезу Н₁, если на самом деле гипотеза Н_о верна. Вероятность ошибки первого рода равна уровню значимости α.

Ошибкой второго рода называется решение принять нулевую гипотезу Н_о, то есть отвергнуть конкурирующую гипотезу Н₁, если на самом деле гипотеза Н₁ верна.

Гипотеза Н₀ проверяется с помощью статистического критерия.

Статистическим критерием (критерием) называют однознач­но определенное правило, устанавливающее условия, при которых проверяемую гипотезу Но следует или отвергнуть, или принять. В ос­нове критерия- функция Т= Т( х1, ..., хn) от выборочных данных (т. е. статистика критерия ), распределение которой известно. Примера­ми таких распределений, на основе которых построено большинство критериев, являются: нормальное, х2(хи-квадрат) - распределение, распределения Стьюдента и Фишера.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотез (об допустимых значений) называют совокупность значений критерия, при кот гипотезу принимают. Критическими называются точки, отделяющие критические области от областей принятия гипотез.

Различают правостороннюю, левостороннюю, двустороннюю критические области Правосторонней критической областью для проверки нулевой гипотезы с уровнем значимости α называется совокупность значений критерия проверки Z, для которых выполняется равенство: P(Z>Z_крит)= α. При этом Z_крит называется границей критической области.

.

Правосторонняя критическая область определяется неравенством: Z> Z_крит.

Левосторонняя критическая область определяется неравенством: Z<- Z_крит.

Односторонней называют правостороннюю или левостороннюю критическую облась.

Двусторонняя критическая область определяется неравенствами Z> Z_1крит и Z> Z_2крит.