Биномиальное распределение, его числовые характеристики.

Биномиальным называется закон распределения дискретной случайной величины X – числа появлений события A в n независимых испытаниях, в каждом из которых появляется либо событие А, либо событие 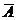, и вероятность появления события А равна p, а вероятность появления события 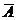равна q=1-p.

Тогда P(X=k) – вероятность появления события А ровно k раз в n испытаниях – вычисляется по формуле Бернулли: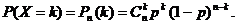

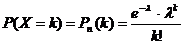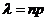Если число испытаний n очень велико, а вероятность p появления события А в каждом испытании очень мала, то для вычисления P(X=k) используют формулу Пуассона: , где . При этом говорят, что случайная величина Ч распределена по закону Пуассона.

Мат ожид этого распредМ=np,а дисперсия D=npq

Распределение Пуассона.

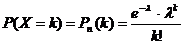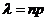Если число испытаний n очень велико, а вероятность p появления события А в каждом испытании очень мала, то для вычисления P(X=k) используют формулу Пуассона: , где . При этом говорят, что случайная величина Ч распределена по закону Пуассона. Мат ожид и дисперсия = лямбда

Теорема Пуассона в теории вероятностей описывает способ получения распределения Пуассона как предел биномиальных распределений.Формулировка

Пусть есть 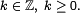Пусть также дана последовательность 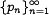такая, что

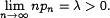
Тогда

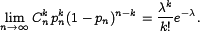
Равномерное распределение, его числовые характеристики.

Равномерным распределением называется распределение таких непрерывных случайных величин, все значения которых лежат на некотором интервале (a;b) и плотность распределения вероятностей задается формулой: 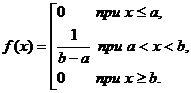. 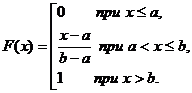- функция распределения вероятностей таких случайных величин.

Мат ожид : М=(а+b)/2 дисперсия: D=(b-а)в квадрате/12

Числовые характеристики непрерывной случайной величины Х, равномерно распределенной в интервале (a;b), вычисляется по формулам: .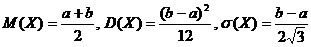

Вероятность попадания величины Ч в промежуток (а₁;а₂), где (а₁;а₂) (a;b), вычисляется по формуле: .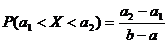

Показательное распределение, его числовые характеристики.

Показательным (или экспоненциальным) называется распределение таких непрерывных случайных величин, у которых функция плотности распределения вероятностей задается формулой: 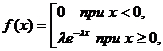, где – некоторое постоянное положительное число.

Функция распределения F(x) таких случайных величин задается формулой: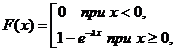

Для непрерывной случайной величины Х, имеющей показательное распределение вероятностей, числовые характеристики вычисляются по формулам: M(X)=1/λ, D(X)=1/ λ², σ(Х)=1/ λ.

Вероятность попадания величины Х в интервал (a;b) вычисляется по формуле: P(a<X<b)=e^-λa-e^-λb.

Мат ожид =1/лямбда,а дисперсия -1/лямбда в квадрате

Нормальное распределение, его числовые характеристики. Выражение функции распределения через интеграл Лапласа. Вероятность попадания нормально распределенной случайной величины в заданный промежуток. «Правило трех сигм».

Нормальным называется распределение вероятностей тех непрерывных случайных величин, у которых плотность распределения задается формулой: 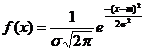где 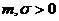– некоторые числа(параметры) Достаточно знать эти параметры, чтобы задать нормальное распределение. Выясним смысл этих параметров и докажем, что m - это математическое ожидание, а сигма-среднеквадратическое отклонение. В зависимости от параметров аист нормальное распределение может называться немного по-разному. Общим называется нормальное распределение с произвольными параметрами м и сигма (сигма>0)

Нормированнымназывают нормальное распределение с параметрами m=0 и сигма=1. Например, если Х-нормальная величина с параметрами m и сигма, то U=(Х-m)/сигма - нормированная нормальная величина, причем, M(U)=0 и сигма(U)=1. Плотность нормированного распределения задается функцией, которая табулирована. Причем, если F(x) - функция общего нормального распределения, a F₀(x) -

функция нормированного распределения, то легко проверить, что F(x)=Fo((x-m)/сигма).

График плотности нормального распределения называют нормальной кривой или кривой Гаусса. Если исследовать эту функцию, видно, что

Изменение величины параметра m не изменяет форму нормальной кривой, а приводит лишь к ее сдвигу вдоль оси ОХ: вправо, если m возрастает и влево, если m убывает.

По иному обстоит дело, если изменяется параметр сигма. Как уже было выяснено, максимум функции плотности нормального распределения равен 1/[сигма(2пи)^1/2]. Поэтому, с возрастанием сигмы максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси ОХ, при убывании сигмы нормальная кривая становится более «островершинной». Важно отметить, что при любых значениях параметров аист, площадь, ограниченная нормальной кривой и осью ОХ остается равной единице (свойство плотности распределения). При m=0 и сигма=1 кривую называют нормированной.

В случае нормального закона распределения функция распределения вероятностей вычисляется по формул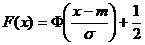е: , где 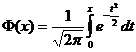– функция Лапласа (или интеграл вероятностей, или функция ошибок).

Числовые характеристики случайной величины Х, заданной нормальным законом распределения, вычисляются по формулам: .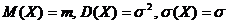

Вероятность того, что случайная величина Х примет значения из интервала (a;b), вычисляется по формуле: .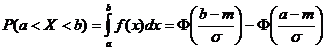

Следствие1: вероятность того, что модуль разности |X-a| меньше некоторого числа δ .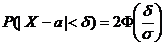

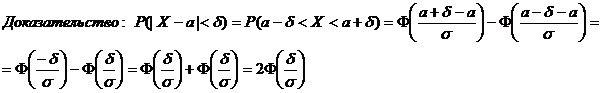
Следствие2: (правило трех сигм): если в следствии1 вместо δ подставить число 3δ, то вероятность того, что модуль разности |X-a|<3δ. На практике правило 3 сигм применяют так:если распределение изучаемой случ вел неизвестно,но условие,указанное в приведенном правиле,выполняется,то есть основание предполагать ,что изучаемая величина распределена нормально.