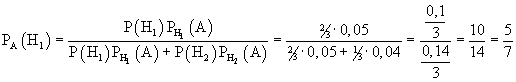Условная вероятность. Теорема умножения вероятностей для зависимых событий.

Теорема умножения вероятностей зависимых событий

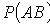
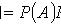
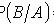
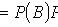
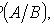
где 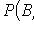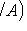- вероятность события B при условии, что произошло событие A.

Пример2. В урне находятся 3 белых, 2 черных и 4 синих шара. Какова вероятность того, что первым будет вынут белый шар, вторым- синий, третьим- черный. Шары не возвращаются.

Решение: Пусть события: А- вынут белый шар, В- вынут синий, С- черный. Вероятность, что первым вынут белый равна

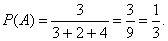
Событие В происходит после события А, при этом условия меняются- общее количество шаров уменьшилось и стало равно 8, поэтому события А и В зависимые и речь идет об условной вероятности события В: Р_А(В)=4/8=1/2. Событие С происходит после событий А и В , поэтому вероятность его тоже условная Р_АВ(С)=2/7. Вероятность же их совместного появления :

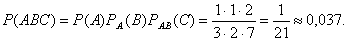
Пример. В группе 20 студентов. Из них двое курят, 12 – в очках, 6 – курят и носят очки. Найти вероятность того, что студент курит, если он носит очки.

Решение. Пусть событие 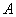- студент курит; 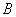- студент носит очки.

Тогда

.

Заметим, что условная и безусловная вероятности события 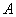в данной задаче различны: .

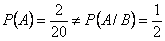Условие независимости событий. Теорема умножения вероятностей для независимых событий

События называются независимыми, если появление одного из них не влияет на вероятность появления другого: .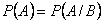

Если события независимые, то теорема умножения вероятностей принимает вид:

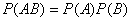- критерий независимости событий.

Формула полной вероятности.

События образуют полную группу, если они в совокупности описывают все возможные несовместные друг с другом исходы некоторого испытания; сумма вероятностей событий полной группы равна 1. Например, испытание - бросание игральной кости. Всего исходов испытания - шесть (число выпавших очков от 1 до 6), каждый может произойти с вероятностью 1/6, сумма вероятностей всех исходов равна 1.
Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

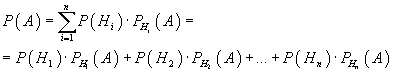
В каждой из двух урн находится 9 белых и 14 чёрных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наудачу один шар. Найти вероятность того, что шар, вынутый из второй урны, окажется чёрным.

Решение
Событие А - шар, вынутый из второй урны, оказался чёрным.
Гипотеза Н₁ - из первой урны во вторую переложили белый шар. Р(Н₁) = 9/23.
Гипотеза Н₂ - из первой урны во вторую переложили чёрный шар. Р(Н₂) = 14/23.
После перекладывания во второй урне стало 24 шара. Условные вероятности события А:

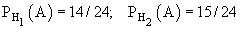
По формуле полной вероятности

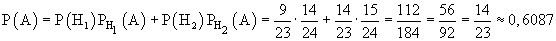
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

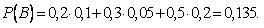
Теорема гипотез (формула Байеса).

Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

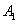- на линию огня вызван первый стрелок,

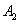- на линию огня вызван второй стрелок,

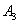- на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то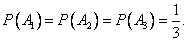

В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

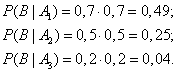
по формуле Байеса находим вероятность гипотезы 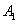после опыта:

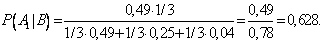
Два цеха штампуют однотипные детали. Первый цех дает 5% брака, второй - 4%. Для контроля отобрано 20 деталей с первого цеха и 10 деталей со второго. Эти детали смешаны в одну партию, и из нее наудачу извлекают одну деталь. Деталь оказалась бракованная. Какова вероятность того, что она из цеха №1?

Решение
Событие А – деталь оказалась бракованной.
Гипотеза Н₁ – деталь изготовлена в 1-м цехе; Р(Н₁) = 2/3
Гипотеза Н₂ – деталь изготовлена во 2-м цехе; Р(Н₂) = 1/3
Условные вероятности события А: P_H1(A)=0,05; P_H2(A)=0,04
Требуется найти вероятность первой гипотезы в предположении, что событие А уже произошло:
P_A(H₁) - ?
Используем формулу вероятности гипотез Бейеса, подставив в знаменатель формулу полной вероятности: