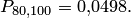Теорема умножения вероятностей для зависимых событий
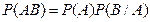
Где 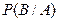 - условная вероятность появления события В, при условии что появилось событие А.
- условная вероятность появления события В, при условии что появилось событие А.
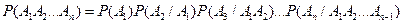
Вероятность появления хотя бы одного события
Пусть события 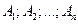 независимые, причем
независимые, причем
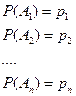
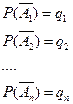
Вероятность появления события А, состоящее в том, что появится хотя бы одно событие 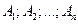 :
:
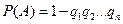
Формула полной вероятности
Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) 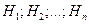 , образующих полную группу событий, равна сумму произведений вероятностей каждой из гипотез на соответствующую условную вероятность появления события А:
, образующих полную группу событий, равна сумму произведений вероятностей каждой из гипотез на соответствующую условную вероятность появления события А:
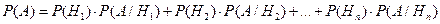
Данная формула называется формулой полной вероятности
Формула Байеса (Бейеса)
Имеется полная группа несовместных гипотез 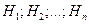 . Вероятности этих гипотез до опыта известны и равны соответственно:
. Вероятности этих гипотез до опыта известны и равны соответственно: 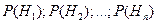 . Произведен опыт, в результате которого наблюдено появление события А. Вероятность того, что появилась i-ая гипотеза, при условии того, что произошло событие А
. Произведен опыт, в результате которого наблюдено появление события А. Вероятность того, что появилась i-ая гипотеза, при условии того, что произошло событие А
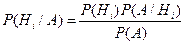 , где вероятность события А находится с помощью формулы полной вероятности
, где вероятность события А находится с помощью формулы полной вероятности
Данная формула и есть формула Байеса (Бейеса).
4)
| Повторение испытаний. Формулы Бернулли, Лапласа, Пуассона |  |  |  |
Пусть А – случайное событие, вероятности появления и непоявления Которого для некоторого испытания известны: 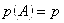 ; ; 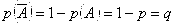 ; ; 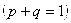 (6.1) И пусть производится не одно, а N повторных испытаний (или, что одно и то же, испытание повторяется N раз). Возникает естественный вопрос: какова вероятность того, что событие А В этих N повторных испытаниях появитсяK раз (целое число K можно задавать любым в пределах от 0 до N)? При этом не важно, в каком порядке событие Апоявится K раз в N испытаниях. Важно лишь общее число K Появлений этого события. Эту вероятность обозначают символом (6.1) И пусть производится не одно, а N повторных испытаний (или, что одно и то же, испытание повторяется N раз). Возникает естественный вопрос: какова вероятность того, что событие А В этих N повторных испытаниях появитсяK раз (целое число K можно задавать любым в пределах от 0 до N)? При этом не важно, в каком порядке событие Апоявится K раз в N испытаниях. Важно лишь общее число K Появлений этого события. Эту вероятность обозначают символом 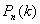 ( ( 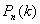 - вероятность того, что в N испытаниях событие А Наступит K раз). И находится она по формуле Бернулли (Яков Бернулли – швейцарский математик 17-го века): - вероятность того, что в N испытаниях событие А Наступит K раз). И находится она по формуле Бернулли (Яков Бернулли – швейцарский математик 17-го века): 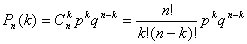 (6.2) Доказательство. Если в N повторных испытаниях событие А появится K Раз, то соответственно оно не появится N-Kраз. И тогда вероятность любой конкретной комбинации K появлений события А и N-K непоявлений этого события можно найти по формуле (4.15) произведения вероятностей независимых в совокупности событий. То есть она равна (6.2) Доказательство. Если в N повторных испытаниях событие А появится K Раз, то соответственно оно не появится N-Kраз. И тогда вероятность любой конкретной комбинации K появлений события А и N-K непоявлений этого события можно найти по формуле (4.15) произведения вероятностей независимых в совокупности событий. То есть она равна 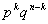 . Таких конкретных комбинаций будет, очевидно, столько, сколько существует сочетаний из N элементов (номеров испытаний) по K элементов в каждом сочетании. Эти сочетания образуются из K номеров тех испытаний, в которых будет появляться событие А. Каждому такому сочетанию K номеров будет соответствовать единственное сочетание тех N-K номеров испытания, в которых событие А не будет появляться. Так как всего таких сочетаний . Таких конкретных комбинаций будет, очевидно, столько, сколько существует сочетаний из N элементов (номеров испытаний) по K элементов в каждом сочетании. Эти сочетания образуются из K номеров тех испытаний, в которых будет появляться событие А. Каждому такому сочетанию K номеров будет соответствовать единственное сочетание тех N-K номеров испытания, в которых событие А не будет появляться. Так как всего таких сочетаний 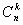 , и каждое из них несовместно с любым другим сочетанием, то по формуле (4.10) сложения вероятностей попарно несовместных событий искомая вероятность равна величине , и каждое из них несовместно с любым другим сочетанием, то по формуле (4.10) сложения вероятностей попарно несовместных событий искомая вероятность равна величине 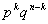 , взятой , взятой 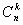 раз. В итоге и приходим к формуле Бернулли (6.2). Пример 1. Монету подбрасывают пять раз подряд. Какова вероятность того, что при этом герб выпадет ровно три раза? Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда N=5 – число повторных испытаний. Далее, будем считать событием А в каждом испытании (при каждом бросании монеты) выпадение герба. Тогда раз. В итоге и приходим к формуле Бернулли (6.2). Пример 1. Монету подбрасывают пять раз подряд. Какова вероятность того, что при этом герб выпадет ровно три раза? Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда N=5 – число повторных испытаний. Далее, будем считать событием А в каждом испытании (при каждом бросании монеты) выпадение герба. Тогда  ; ; 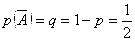 ; N=5; K=3; ; N=5; K=3; 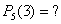 На основании формулы Бернулли получаем: На основании формулы Бернулли получаем: 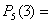 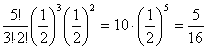 . Формула Бернулли – точная формула. Однако при больших значениях N (большом числе испытаний) вычисления по ней становятся громоздкими из-за необходимости вычисления факториалов больших чисел и степеней с большими показателями. В процессе этих вычислений неизбежно придется производить округления, что приведет к погрешности при определении искомой вероятности . Формула Бернулли – точная формула. Однако при больших значениях N (большом числе испытаний) вычисления по ней становятся громоздкими из-за необходимости вычисления факториалов больших чисел и степеней с большими показателями. В процессе этих вычислений неизбежно придется производить округления, что приведет к погрешности при определении искомой вероятности 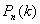 . Причем к погрешности тем большей, чем больше будет значение N (числа испытаний). В связи с этим из формулы Бернулли выведены упрощенные приближенные формулы для . Причем к погрешности тем большей, чем больше будет значение N (числа испытаний). В связи с этим из формулы Бернулли выведены упрощенные приближенные формулы для 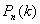 , которые, кстати, тем точнее, чем больше число N. , которые, кстати, тем точнее, чем больше число N. |
Другой приближенной формулой для подсчета вероятностей 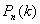 , применяемой при больших N, является Формула Пуассона (формула редких событий):
, применяемой при больших N, является Формула Пуассона (формула редких событий):
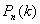
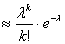 , где
, где 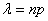 (6.6)
(6.6)
Она применяется, когда N Велико (условно N 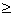 50), а Р мало (0<Р<0,1), и когда Npq<10. То есть когда не оправдано ни применение формулы Бернулли, ни применение локальной формулы Лапласа. При этих условиях приближенная формула Пуассона, как и локальная формула Лапласа, обеспечивает определение искомой вероятности
50), а Р мало (0<Р<0,1), и когда Npq<10. То есть когда не оправдано ни применение формулы Бернулли, ни применение локальной формулы Лапласа. При этих условиях приближенная формула Пуассона, как и локальная формула Лапласа, обеспечивает определение искомой вероятности 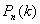 С погрешностью в пределах одного процента.
С погрешностью в пределах одного процента.
Кстати, так как вероятность 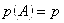 события А Мала (0<Р<0,1), то при повторении испытаний событие А наступает редко. Поэтому формула Пуассона и называется формулой редких событий. Вывод этой формулы опустим.
события А Мала (0<Р<0,1), то при повторении испытаний событие А наступает редко. Поэтому формула Пуассона и называется формулой редких событий. Вывод этой формулы опустим.
Пример 3. Производится 50 повторных испытаний, причем вероятность появления некоторого события А В каждом из них равна 0,98. Определить вероятность того, что событие А наступит во всех 50 испытаниях.
Решение. В данной задаче
P(A)=P=0,98; P(Ā)=Q=0,02; N=50; K=50; 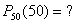
Если применить формулу Бернулли, то получим результат, который очевиден и без формулы Бернулли:
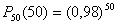
Попробуем избежать громоздкой процедуры возведения числа 0,98 в 50-ую степень (её, впрочем, можно и избежать, если использовать логарифмы). То есть заменим формулу Бернулли на локальную формулу Лапласа или Пуассона.
Так как Npq=50·0,98·0,02=0,98<10, то локальную формулу Лапласа применять нельзя - мы получим слишком грубый (неточный) результат. Но и формулу Пуассона (формулу редких событий) мы тоже применить не можем, так как вероятность Р не мала, а наоборот, велика. Но зато мала вероятность Q непоявления этого события. В связи с этим переформулируем задачу: найдем вероятность 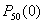 того, что событие
того, что событие 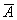 появится 0 раз (ни разу). Эта вероятность, очевидно, совпадает с искомой вероятностью
появится 0 раз (ни разу). Эта вероятность, очевидно, совпадает с искомой вероятностью 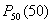 Того, что событие А появится во всех 50 испытаниях. Тогда в этой постановке получаем:
Того, что событие А появится во всех 50 испытаниях. Тогда в этой постановке получаем:
P(Ā)=P=0,02; P(A)=Q=0,98; N=50; K=0; 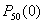 ?
?
Применяя формулу Пуассона (теперь ее применять можно), получим:
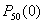 ≈
≈ 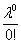
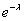 = |λ=Np=50·0,02=1| =
= |λ=Np=50·0,02=1| = 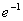 =
= 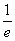 ≈
≈ 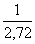 ≈ 0,37.
≈ 0,37. 
Локальная теорема Лапласа
Пользоваться формулой Бернулли при больших значениях 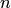 очень трудно. Например, если
очень трудно. Например, если 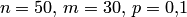 , то для отыскания вероятности
, то для отыскания вероятности 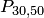 надо вычислить значение выражения
надо вычислить значение выражения
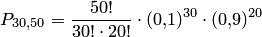
Естественно, возникает вопрос: нельзя ли вычислить интересующую вероятность, не используя формулу Бернулли? Оказывается, можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления событий ровно 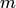 раз в
раз в 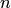 испытаниях, если число испытаний достаточно велико.
испытаниях, если число испытаний достаточно велико.
Теорема 3.1. Если вероятность 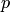 появления события
появления события 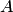 в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 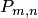 того, что событие
того, что событие 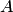 появится в
появится в 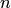 испытаниях ровно
испытаниях ровно 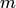 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 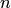 ) значению функции
) значению функции
при 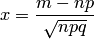 .
.
Существуют таблицы, которые содержат значения функции 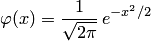 , соответствующие положительным значениям аргумента
, соответствующие положительным значениям аргумента 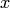 . Для отрицательных значений аргумента используют те же таблицы, так как функция
. Для отрицательных значений аргумента используют те же таблицы, так как функция 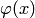 четна, т. е.
четна, т. е. 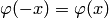 .
.
Итак, приближенно вероятность того, что событие 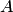 появится в
появится в 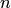 испытаниях ровно
испытаниях ровно 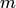 раз,
раз,
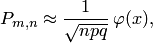 где
где 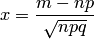 .
.
Пример 3. Найти вероятность того, что событие 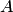 наступит ровно 80 раз в 400 испытаниях, если вероятность появления события
наступит ровно 80 раз в 400 испытаниях, если вероятность появления события 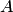 в каждом испытании равна 0,2.
в каждом испытании равна 0,2.
Решение. По условию 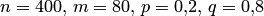 . Воспользуемся асимптотической, формулой Лапласа:
. Воспользуемся асимптотической, формулой Лапласа:
Вычислим определяемое данными задачи значение 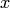 :
:
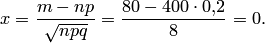
По таблице прил, 1 находим 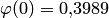 . Искомая вероятность
. Искомая вероятность
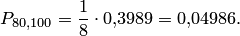
Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):