Методом статистического последовательного анализа

Описывается некоторое событие А, которое может произойти или не произойти в результате повторных независимых испытаний (эксперимен­тов). Примером такого события может служить попадание выборочного значения в интервал с заданными границами , как это было в разд. 2.7.4. Проверяется гипотеза о вероятности 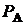события А:

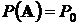: против альтернативы : .

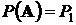В процессе испытаний после каждого из них ведется подсчет количества k случаев, когда, например, событие A не произошло, и это количество сравнивается со значениями, которые лежат на двух прямых линиях:

,

,

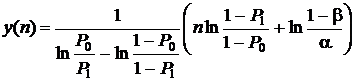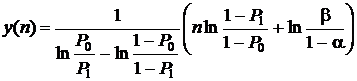где a и b–вероятности ошибочных решений первого и второго рода соответственно, которые обеспечиваются, если каждая из них не превышает 0,15.

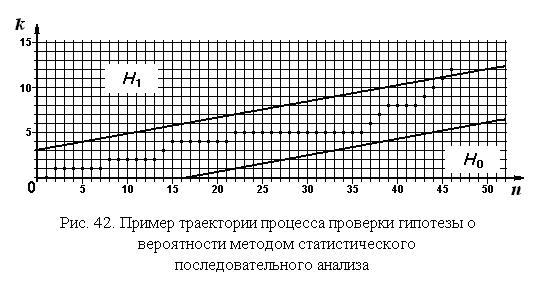
Пример таких прямых приведен на рис. 42. Они параллельны. Часть плоскости, лежащая над верхней прямой, – зона отклонения нулевой гипотезы. Часть плоскости, лежащая под нижней прямой, – зона принятия нулевой гипотезы. Зона между ними называется зоной безразличия. Ее ширина определяется вероятностями a и b, а также разностью между вероятностями 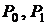. Для того, чтобы применить последовательный анализ к проверке сложной гипотезы об интерквантильном промежутке, описанной в разд. 2.7.5, ее нужно преобразовать к проверке простой гипотезы. В качестве 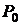следует принять 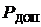и взять .

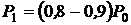Процесс последовательной проверки сформулированной гипотезы отображается на координатной плоскости (см. рис. 42) ступенчатой траекторией точки с координатами (n, k), где n – номер очередного испытания (эксперимента), k – суммарное количество случаев неосуществления события A. Испытания продолжаются до тех пор, пока эта траектория не выйдет в зону той или иной гипотезы.

А. Вальдом [8] доказано, что при неограниченном количестве испытаний процесс заканчивается с вероятностью 1. Однако на практике количество испытаний ограничено по экономическим, техническим и иным причинам. Поэтому при выходе на ограничение приходится принимать то или иное решение в зависимости от того, какого рода риск (первого или второго) более оправдан.

Преимущество статистического последовательного анализа перед подходом, изложенным в разд. 2.7.4, состоит в том, что здесь гипотеза проверяется при каждом новом результате непосредственно в процессе испытаний, и за счет этого общая трудоемкость в среднем по множеству подобных процессов уменьшается.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основной

1. Гмурман В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман.– М. : Высш. шк., 2008.

2. Ивановский Р. И. Теория вероятностей и математическая статистика / Р. И. Ивановский.– СПб. : БХВ-Петербург, 2008.

3. Коваленко И. Н. Теория вероятностей и математическая статистика / И. Н. Коваленко, А.А.Филиппова.– М. : Высш. шк., 1973.

Дополнительный

4. Крамер Г. Математические методы статистики / Г. Крамер.– М. : Мир, 1975.

5. Рао С. Р. Линейные статистические методы и их применение / С. Р. Рао.–М. : Наука. 1968.

6. Уилкс С. Математическая статистика / С. Уилкс.– М. : Наука, 1967.

7. Дрейпер Н. Прикладной регрессионный анализ. Т. 1,2 / Н. Дрейпер, Г. Смит.– М. : Финансы и статистика, 1987.

8. Вальд А. Последовательный анализ / А. Вальд.– М. : Физматгиз, 1960.

9. Башаринов А. Е. Методы последовательного статистического анализа и их приложения / А. Е. Башаринов, Б. С. Флейшман.– М. : Сов. Радио, 1962.

10. Эфрон Б. Нетрадиционные методы многомерного анализа / Б. Эфрон. – М. : Финансы и статистика. 1960.

11. Подборка статей по методу бутстреп // Заводская лаборатория. – 1987. № 10.

12. Климов Г. П. О фидуциальном подходе в статистике // Доклады АН СССР.– 1970.– т. 191, № 4.– с. 763-765.

13. Большев Л. Н. Таблицы математической статистики / Л. Н. Большев, Н. В. Смирнов; ВЦ АН СССР. М., 1968.

14. Оуэн Д. Б. Сборник статистических таблиц / Д. Б. Оуэн; ВЦ АН СССР. М., 1966.

15. Максимов Ю.Д. Математика. Вып. 6. Теория вероятностей. Контрольные задания с образцами тестов / Ю.Д. Максимов, .А. Б. Куклин, Ю. А. Хватов. –СПб.: Изд-во СПбГПУ, 2008.

[1] Bootstrep (англ) – петля на верхней части голенища сапога, с помощью которой этот сапог надевается