Кондиционирование результатов экспериментов

Пусть случайная величина x непрерывна. В этом случае все выборочные значения будут различны.

После получения выборочных значений случайной величины в хронологическом порядке первым шагом в их обработке является сортировка в порядке возрастания. Это действие осуществляется автоматически при расстановке выборочных значений на числовую ось. Порядковые номера выборочных значений изменяются, и новые порядковые номера указываются в скобках:

.

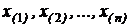Выборка, отсортированная таким образом, называется вариационным рядом, отдельные элементы – членами вариационного ряда. Первый и последний члены называются крайними членами вариационного ряда. Если количество членов вариационного ряда нечетное, то существует единственный средний член вариационного ряда, номер которого (2n + 1)/2 . Средний член вариационного ряда называется выборочной медианой.

Следующий шаг – построение выборочной функции распределения 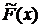, которая является оценкой генеральной функции распределения F(x). Пример выборочной функции распределения приведен на рис. 26.

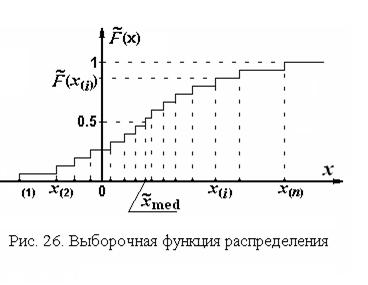Выборочная функция распределения изображается ступенчатой линией. Абсциссами каждого скачка этой линии являются выборочные значения 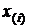. Высота всех ступеней одинакова и равна 1/n. Такое построение выборочной функции распределения основано на результате, полученном в примере 3 разд. 1.6.7.

В самом деле, при каждом значении 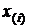ординатами каждой ступени являются значения выборочной функции распределения 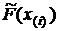. На множестве экспериментов, повторяющихся в неизменных условиях, выборочные значения являются случайными величинами, распределенными так же, как и генеральная совокупность, из которой они извлекаются, то есть F(x) – их функция распределения. А это значит, что реализуются условия упомянутого примера, из которого следует, что значения 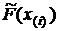, которые являются случайными на множестве повторяющихся экспериментов, распределены равномерно в интервале [0, 1]. Поэтому высота всех ступенек принята одинаковой.

Оценкой плотности распределения является гистограмма. По сути дела, гистограмма является выборочной плотностью распределения, и в отличие от генеральной плотности распределения j(x) мы обозначим ее 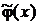. Пример гистограммы приведен на рис. 27.

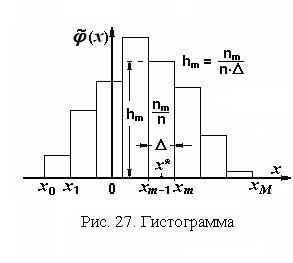Для построения гистограммы интервал между крайними членами вариационного ряда делится на M интервалов 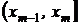равной длины D = 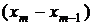. Подсчитывается количество 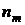выборочных значений, попавших в каждый m-й интервал и вычисляется частость 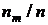, которая является оценкой вероятностной меры каждого интервала. Количество интервалов или их ширина выбирается таким образом, чтобы самый “бедный” интервал содержал 3¸5 выборочных значений. Для удобства построения гистограммы и последующих вычислений рекомендуется округлить значение ширины интервалов до ближайшего удобного числа. Далее на полученных интервалах, как на основаниях строятся прямоугольники, высота каждого из которых должна быть

.

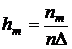Только при таком построении площадь гистограммы будет равна единице, точно так же, как и под генеральной плотностью распределения, оценкой которой является гистограмма. В самом деле,

.

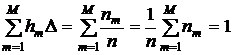Следует обратить внимание на то, что за счет группирования выборочных данных при построении гистограммы часть информации о случайной величине, содержащейся в выборочных данных, теряется. Напротив, выборочная функция сохраняет в себе всю информацию, содержащуюся в выборочных данных.

ТОЧЕЧНОЕ ОЦЕНИВАНИЕ

Точечной статистической оценкой называется оценка числовой характеристики или параметра генеральной совокупности, выражаемая одним числом.

Оценивание квантилей

Оценивание квантилей выполняется по выборочной функции распределения, по сути дела, графическим способом. Это можно показать на примере точечного оценивания медианы, то есть 50%-ной квантили 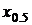. Для этого по заданной вероятности q = 0,5 на графике выборочной функции распределения (рис. 26) проводят горизонтальную прямую до ее пересечения с выборочной функцией распределения. Абсцисса точки пересечения есть искомая оценка 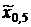, которая является выборочной медианой 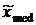. Этой абсциссой при нечетном n = 2k + 1 обязательно окажется, по построению, выборочное значение – средний член вариационного ряда .

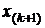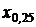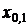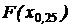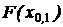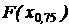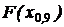Для оценки других квантилей, например, квартили или децили горизонтальные линии проводят на уровне вероятности =0,25 или = 0,1 соответственно. Так же находятся точечные оценки высоковероятных квантилей или . Из графика (см. рис. 26) видно, что абсциссой пересечения выборочной функции распределения с любой горизонтальной прямой обязательно окажется одно из выборочных значений. И здесь необходимо обратить внимание на следующее обстоятельство.

Пусть необходимо оценить квантиль 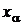при 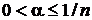или квантиль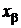 при 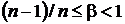. При задании вероятностей a и b из указанных промежутков оценками соответствующих квантилей неизменно окажется первый или последний член вариационного ряда независимо от заданных значений вероятностей, что будет свидетельствовать о крайне низкой достоверности этих оценок. Для того чтобы не сталкиваться с подобной ситуацией, необходимо установить минимально допустимый объем выборки, обеспечивающий достаточную достоверность получаемых оценок квантилей в зависимости от задаваемой вероятности. Эту задачу решим, исходя из приведенных неравенств:

при задании значения вероятности, не превышающего 0,5

;

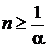при задании значения вероятности, превышающего 0.5

.

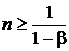Так, например, если задана вероятность a = 0,05, то для точечного оценивания квантили 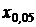объем выборки не должен быть меньше 20. Если задана вероятность b = 0,99, то для точечного оценивания квантили 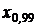объем выборки не должен быть меньше 100. Рекомендуется увеличивать объем выборки сверх минимального, указанного этими неравенствами, чтобы застраховаться от возможных грубых промахов измерений, которые могут быть вызваны импульсными помехами или сбоями аппаратуры.

Пусть стоит задача получить точечные оценки границ интерквантильного промежутка 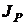. Как следует из разд. 1.6.2, генеральными граничными квантилями этого промежутка являются 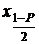и 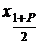. Поэтому точечное оценивание границ интерквантильного промежутка состоит в поочередном оценивании каждой из этих квантилей при соблюдении указанных ранее соотношений и рекомендаций относительно необходимого объема выборки, то есть

для оценки нижней границы ;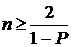

для оценки верхней границы также .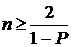

В частности, если заданоP = 0,95, то минимальный объем выборки составит 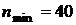.