Непрерывных случайных величин

1.6.6.1. Случайная величина – интервал времени между импульсами

в простейшем потоке

Простейший случайный поток импульсов, заявок на обслуживание и тому подобных последовательностей случайных событий задается следующими свойствами:

поток импульсов (заявок) рассматривается в течение интервала времени, равного t;

в любом бесконечно малом, но не нулевом промежутке времени Dt, на которые поделен интервал времени (0, t] и который будем называть элементарным промежутком, с вероятностью p > 0 может появиться только один импульс (одна заявка);

появление импульса (заявки) в каждом из элементарных промежутков времени Dt есть событие, не зависящее от предыстории, то есть от появления импульса (заявки) в преды­дущие промежутки времени, это свойство –отсутствие последействия, или отсутствие памяти.

Такие условия осуществления событий, которые заключаются в случайном появлении импульсов (заявок) в следующие друг за другом элементарные промежутки времени, в точности соответствуют схеме Бернулли последовательности независимых испытаний (см. разд. 1.3.2). Если n– количество элементарных промежутков на интервале (0, t],то t = nDt, а np – математическое ожидание количества импульсов (заявок) на этом интервале (то есть среднее значение их количества). Тогда естественным образом может быть вычислена средняя частота или интенсивность следования импульсов (заявок) в течение интервала (0, t] как отношение среднего их количества за этот интервал к длительности интервала: 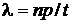. Отсюда, в частности, следует, что np = lt.Единица измерения частоты l – [1/c] .

Найдем функцию распределения непрерывной случайной величины t–времени между двумя последовательными импульсами (заявками) в потоке:

.

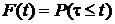Неравенство 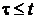выполняется, когда за время t появляется один импульс (заявка), или два импульса (заявки), или три импульса (заявки) и т. д. Определить вероятность бесконечного объединения подобных событий затруднительно. Гораздо легче и продуктивнее определить эту вероятность через вероятность противоположного события, а именно, через вероятность того, что за время t не появится ни одна заявка (отказ, импульс), то есть

.

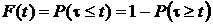Напомним, что исходной моделью для модели простейшего потока была схема независимых испытаний Бернулли (см. разд. 1.3.2). Поскольку потоки указанных событий реализуются в непрерывном времени, устремим Dt к нулю (при этом n ® ¥ , 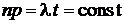), и с использованием теоремы Пуассона (см. разд.1.3.6) найдем вероятность появления m импульсов в n интервалах времени, или, что то же самое, в течение времени t, как предел :

.

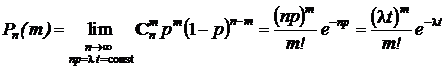Вероятность того, что в течение времени t не появится ни один импульс (или ни одна заявка), то есть m = 0, равна 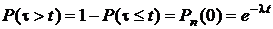. Отсюда функция распределения интервала времени между двумя последовательными импульсами (заявками) в случайном потоке

.

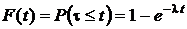Плотность распределения этой случайной величины есть производная от F(t) по t:

.

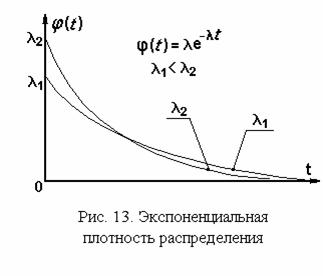
В результате мы получили экспоненциальную плотность распределения или экспоненциальный закон распределения.

Вид кривой экспоненциальной плотности распределения при различных значениях параметра l представлен на рис. 13. Фигуры, ограниченные кривой плотности распределения и осью абсцисс, равновелики, их площади равны 1. Характеристическая функция экспоненциального распределения вычисляется, по определению (разд. 1.6.4), как интеграл:

.

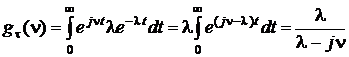Математическое ожидание и дисперсию случайного интервала времени между событиями (заявками, отказами, импульсами) находим, пользуясь свойствами характеристических функций:

,

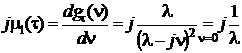откуда ;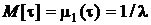

,

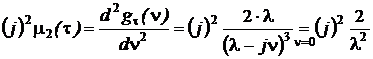откуда 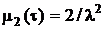и 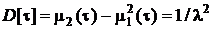. Значит, среднеквадратическое значение .

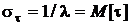При статистической обработке экспериментальных данных, когда возникает необходимость идентификации вида плотности распределения исследуемой случайной величины, последнее соотношение может служить одним из признаков экспоненциального распределения.

Сформированная таким образом математическая модель случайной последовательности событий называется простейшим потоком или потоком Пуассона и применяется в теории массового обслуживания и в теории надежности для вероятностного описания, например:

потока вызовов на телефонную станцию;

потока обращений к серверу коллективного пользования в компьютерной сети;

потока автомобилей на пограничный пункт таможенного досмотра;

потока клиентов на обслуживающее предприятие;

потока отказов технического устройства и т.д.

Наряду с простейшим потоком в теории массового обслуживания используются и более сложные модели потоков заявок, например, потоки Эрланга и Пальма, однако наиболее полные аналитические описания всех процедур и характеристик обслуживания заявок, потоков необслуженных заявок, длины очередей на обслуживание и тому подобных характеристик существуют пока только для простейших потоков.

В теории надежности F(t) называется функцией распределения времени безотказной работы устройства, а вероятность P(t) = 1 – F(t)= 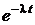– функцией надежности.

Математические модели случайных потоков событий применяются для анализа и синтеза систем, в которых подобные потоки возникают. Целью анализа и расчета таких систем может быть, например:

оценка вероятности того, что обслуживание заявки не состоится, и заявка пропадает;

оценка средней длины очереди заявок на обслуживание;

анализ и синтез стратегии обслуживания заявок;

расчет времени безотказной работы сложных систем и т.д.

1.6.6.2. Равномерная плотность распределения

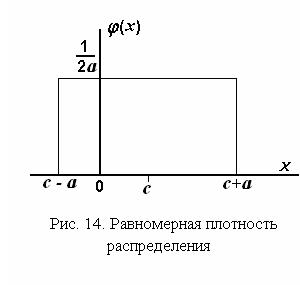Вид плотности распределения представлен на рис. 14. Аналитическая запись плотности распределения:

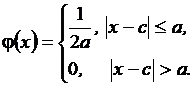
Видно, что условие нормировки соблюдены, поскольку площадь под плотностью распределения равна 1.

Плотность распределения симметрична относительно математического ожидания,

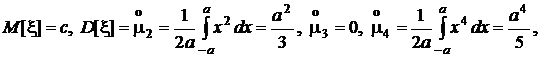
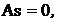
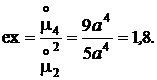
Дифференциальная энтропия .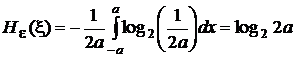

Случайная величина с равномерной плотностью распределения экстремальна по энтропии в следующем смысле.

Пусть о случайной величине известно лишь то, что значения, которые она может принимать, ограничены по модулю некоторым числом A, то есть 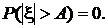Тогда среди всех таких случайных величин максимальной относительной энтропией обладает случайная величина с равномерной плотностью распределения.

1.6.6.3. Плотность распределения Arcsin

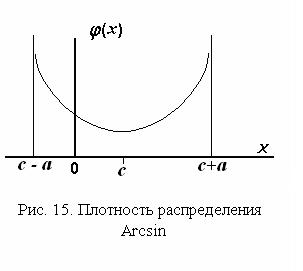График плотности распределения приведен на рис. 15. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией

.

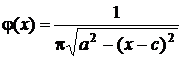Математическое ожидание и медиана совпадают:

.

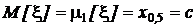Дисперсия, четвертый центральный момент, асимметрия и эксцесс:

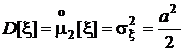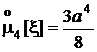, , As = 0,

.

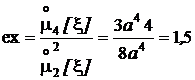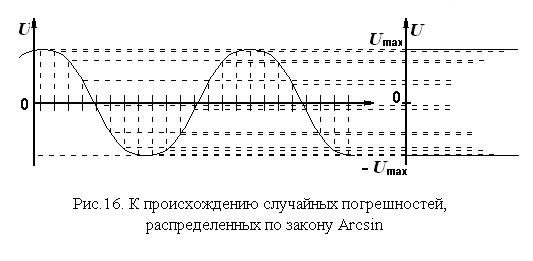
Случайная величина с такой плотностью распределения возникает при аналого-цифровом преобразовании, например, синусоидального напряжения, действующего на входе аналого-цифрового преобразователя (АЦП). При запуске АЦП в случайные моменты времени или в моменты времени, не синхронизированные с частотой напряжения помехи (см. рис. 16), из-за плоских максимумов и минимумов синусоиды плотность значений выходного сигнала АЦП возрастает к краям интервала и минимальна в середине этого интервала. Интегральная функция распределения описывается функцией, обратной функции y = sin x, то есть функцией

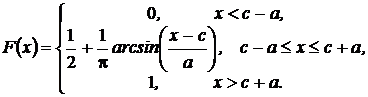
1.6.6.4. Нормальная плотность распределения (Гаусса)

Кривая нормальной плотности распределения описывается функцией

,

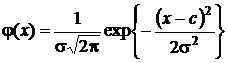которая называется гауссианой по имени германского математика К. Ф. Гаусса. Позднее были открыты многие замечательные свойства случайных величин, распределенных по нормальному закону. Мы познакомимся с большинством этих свойств.

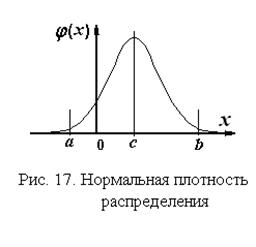
Форма кривой нормальной плотности представлена на рис. 17. Это симметричная одномодальная плотность распределения, поэтому математическое ожидание, мода и медиана совпадают:

.

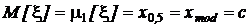Дисперсия, четвертый центральный момент, асимметрия и эксцесс:

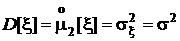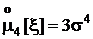, , As = 0, .

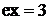В некоторых источниках эксцесс плотности распределения определяют по отношению к эксцессу нормальной плотности распределения. Тогда эксцесс любого распределения уменьшается на 3, а эксцесс нормального распределения равен 0:

.

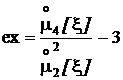Дифференциальная энтропия нормально распределенной случайной величины

.

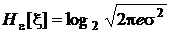Случайная величина с нормальной плотностью распределения экстремальна по энтропии в смысле следующей задачи. Пусть о случайной величине известно, что 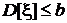, где b – любое положительное конечное число. Найти плотность распределения, при которой дифференциальная энтропия этой случайной величины достигает максимального значения на множестве всех плотностей распределения.

Задача решается методами вариационного исчисления. Единственное решение задачи – нормальная плотность распределения. Иными словами, среди случайных величин, о которых известно лишь то, что дисперсия каждой из них ограничена одним числом, максимальной энтропией обладает случайная величина, распределенная нормально.

Принадлежность случайной величины к нормальной генеральной совокупности с математическим ожиданием c и дисперсией 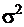будем обозначать следующим образом

.

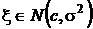Характеристическую функцию нормальной случайной величины приведем здесь без вывода:

.

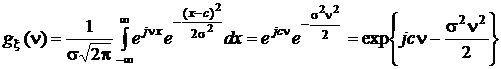Обратим внимание на то, что при отсутствии сдвига плотности распределения относительно начала координат, то есть при c = 0, множитель 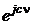пропадает.

Интегральная функция нормального распределения выражается интегралом от плотности распределения:

.

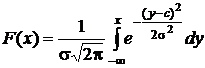Этот интеграл не может быть записан в конечной форме, поэтому его значения табулируются. В связи с тем, что этот интеграл зависит от параметров с и 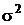, которые могут принимать бесчисленное множество значений, в целях удобства табулирования эти параметры исключаются путем замены переменной интегрирования:

.

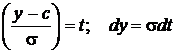Тогда, пользуясь тем, что нормальная плотность распределения симметрична и F(c)=0,5, получим для :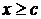

= ,

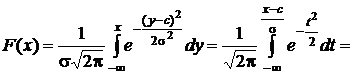
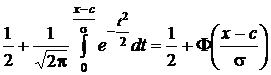где функция

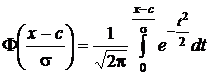
называется функцией Лапласа.

Таблицы этой функции приводятся во всех без исключения справочниках, учебниках и учебных пособиях по теории вероятностей и математической статистике. Если 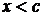, 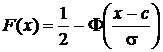. Оба эти выражения распространяются на всю ось путем объединения с использованием знаковой функции sign[·] :

.

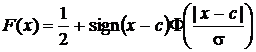Вероятностная мера полуоткрытого интервала (a, b] вычисляется, как

.

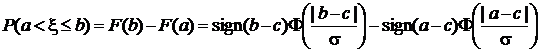Если интервал симметричен относительно математического ожидания, то есть границы интервала (c - a, c + a], то

.

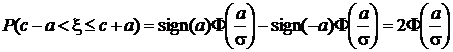На практике часто используются интервалы, ширина которых исчисляется целыми значениями среднеквадратического отклонения s. Наиболее популярными среди них являются : a = s, a = 2s, a = 3s. Для этих значений 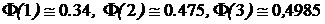. Соответственно вероятностные меры интервалов

, ,

.

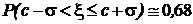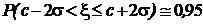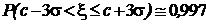Приведем два из многих исключительных свойств нормального распределения вероятностей: интегральную теорему Муавра – Лапласа и центральную предельную теорему (ЦПТ).

Интегральная теорема Муавра-Лапласа основывается на локальной теореме Муавра-Лапласа, которая сообщена выше в разд. 1.3.7.

Напомним, что если в схеме Бернулли (см. разд. 1.2.4) количество испытаний возрастает, то есть n ® ¥, а вероятность p появления одного из двух противоположных событий не изменяется, то в соответствии с локальной теоремой Муавра – Лапласа .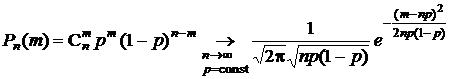

Интегральная теорема Муавра – Лапласа посвящена задаче упрощенной оценке вероятности 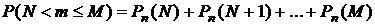без необходимости трудоемких вычислений числа сочетаний.

На основании локальной теоремы

.

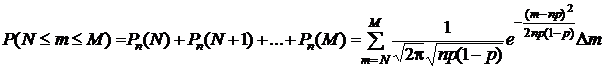Последнее равенство является точным в условиях действия локальной теоремы Муавра – Лапласа в связи с тем, что из-за дискретности случайной величины 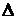m = 1. В то же время последняя сумма есть не что иное, как формула прямоугольников приближенного вычисления интеграла:

.

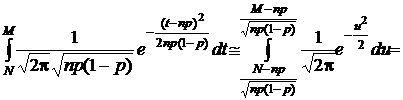
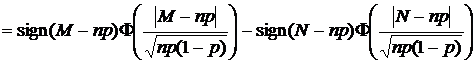В конечном итоге при n ® ¥и p = const интегральная теорема Муавра – Лапласа утверждает следующую асимптотику:

.

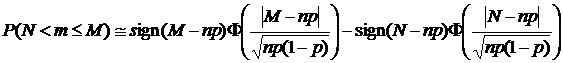Центральная предельная теорема (ЦПТ). Приведем упрощенную формулировку теоремы.

Плотность распределения суммы независимых произвольно распределенных случайных величин, дисперсии которых различаются не слишком сильно, при увеличении числа слагаемых стремится к нормальной плотности распределения.

Более точная формулировка приводится, например, в книге [6] на стр. 268.

1.6.6.5. Плотность распределения Лапласа

График плотности распределения приведен на рис. 18. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией

.

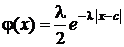Математическое ожидание и медиана совпадают:

.

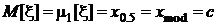Для определения дисперсии воспользуемся характеристической функцией. Поскольку плотность распределения Лапласа симметрична и центральные моменты не зависят от смещения плотности распределения, примем с = 0. Тогда характеристическая функция получается из выражения

.

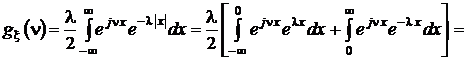
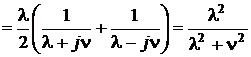Если с ¹ 0, то в соответствии со свойством б) характеристических функций (см. разд. 1.6.4) появится экспоненциальный множитель

.

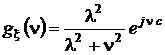По свойству характеристических функций при с = 0

,

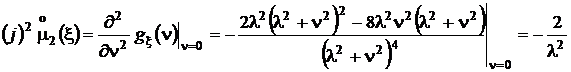откуда следует, что дисперсия .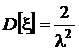

Четвертый центральный момент, асимметрия и эксцесс:

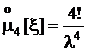, As = 0, .

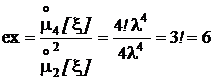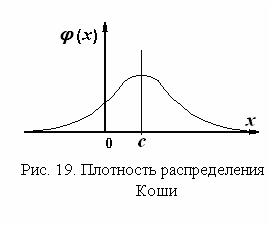
1.6.6.6. Плотность распределения Коши

График плотности распределения приведен на рис. 19. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией

.

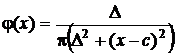Плотность распределения симметрична, одномодальна.

Из общего выражения для моментов

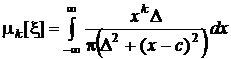
видно, что при всех целых значениях k > 0этот несобственный интеграл не существует, поскольку порядок убывания подынтегральной функции на бесконечности при k > 0не превышает 1. При k=0 этот интеграл равен 1, что и должно следовать из условия нормировки плотности распределения.

В связи с этим математическое ожидание, дисперсия и моменты более высоких порядков случайной величины, распределенной по Коши, отсутствуют. Параметры плотности распределения Коши имеют названия: c – параметр сдвига (совпадает с модой и медианой), D – параметр масштаба.

Эксцесс случайной величины, распределенной по Коши, равен ¥.

Характеристическая функция

.

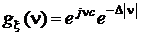Справедливость этого выражения обнаруживается при сопоставлении пары преобразований Фурье, связывающих плотность распределения Лапласа с ее характеристической функцией при c = 0. Здесь вид характеристической функции с точностью до множителя совпадает с видом плотности распределения Лапласа, а вид характеристической функции плотности Лапласа с точностью до того же множителя совпадает с видом плотности распределения Коши.

Заметим, что характеристическая функция случайной величины, распределенной по Коши, недифференцируема в нуле, и это еще один признак отсутствия моментов данной случайной величины.

1.6.6.7. Экспоненциальное семейство распределений

Представляемое здесь семейство плотностей распределений описывается функцией:

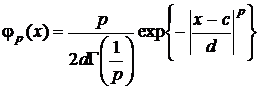,где ,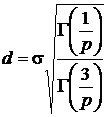

p – параметр семейства, G[·]–гамма-функция (будет представлена в разделе 1.6.6.8). Все плотности распределения семейства симметричны, математическое ожидание совпадает с медианой и модой и равно c , эксцесс плотностей семейства равен

.

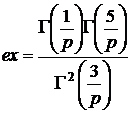При p = 1 членом этого семейства является плотность распределения Лапласа, при p = 2 – нормальная плотность распределения.

В самом деле, при p = 1 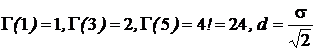и плотность распределения приобретает вид

,

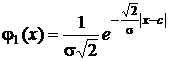а это и есть плотность распределения Лапласа, параметр которой в этом случае 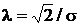, ex = 6.

При p = 2 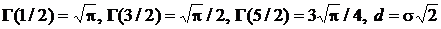и плотность распределения принимает вид:

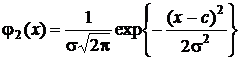, ex = 3,

что и требовалось показать.

При дальнейшем увеличении параметра p плотность распределения приобретает форму, приближающуюся к форме равномерной плотности. При этом все плотности семейства симметричные с математическим ожиданием, равным c.