И плотность распределения вероятностей

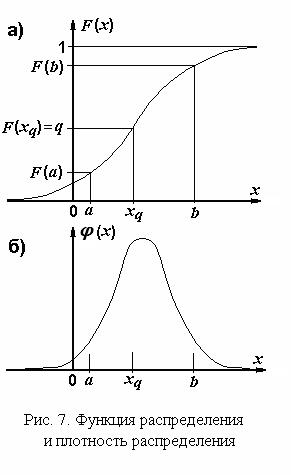
Пусть случайная величина задана тройкой ( 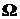, Â,P).Будем обозначать случайные величины греческими буквами, а значения, которые они принимают – соответствующими латинскими. Например, если случайная величина обозначена буквой x, то значения, которые она принимает, будем обозначать буквой x.

Математическое определение (интегральной) функции распределения непрерывной случайной величины (обычно слово “интегральной” из этого термина опускают): .

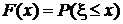Понятно, что эта функция неотрицательна и не убывает на всей оси. Область значений функции распределения – [0, 1]. Пример графика функции распределения непрерывной случайной величины показан на рис. 7 а.

Представим полуоткрытый интервал (-¥, b], как объединение двух непересекающихся полуоткрытых интервалов :

(-¥, b] = (-¥, а] 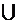(a, b].

Тогда в связи с аддитивностью вероятностной меры

= ,

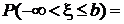
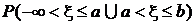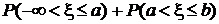и, по определению функции распределения,

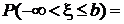F(b)=F(a)+ .

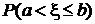Отсюда следует, что 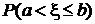= F(b)-F(a).

Механической аналогией, удобной для понимания смысла функции распределения непрерывной случайной величины, может служить ось с переменной плотностью материала, из которого она изготовлена. Тогда механическим аналогом функции распределения может служить зависимость веса левого отрезка оси от координаты разреза. Последнее выражение показывает, что вес отрезка оси, вырезанного из середины, равен разности между весом отрезка (-¥, b] и отрезка (-¥, a].

Встав на путь механических аналогий, мы не можем не заинтересоваться такой характеристикой, как удельный вес или плотность материала оси, тем более что плотность изменяется по длине оси, то есть плотность есть функция от x:j(x).

По определению плотности (или удельного веса) бесконечно тонкого стержня,

.

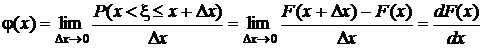Функция j(x) называется плотностью распределения вероятностей или законом распределения вероятностей непрерывной случайной величины. Она представлена на рис. 7, б). Поскольку функция распределения – неубывающая функция, j(x) 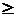0.

Для плотности распределения справедливы следующие соотношения:

, ,

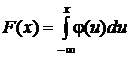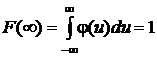где u так же, как x – значения, которые может принимать случайная величина x.

Последнее из этих соотношений является условием нормировки плотности распределения вероятностей.

Вероятность того, что в результате испытания случайная величина примет значение из полуоткрытого интервала (a, b], то есть вероятностная мера этого интервала, вычисляется как площадь криволинейной трапеции, находящейся под кривой плотности распределения над этим интервалом:

.

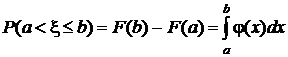Таким образом, площадь под всей кривой плотности распределения есть вероятность достоверного события, которое заключается в том, что в результате испытания случайная величина примет какое-либо значение.

Кроме того, из приведенных соотношений следует, что событие x = с невозможно, поскольку вероятность того, что в результате испытания непрерывная случайная величина примет конкретное значение, равна нулю:

.

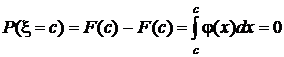Иными словами, это означает, что в условиях, когда определена непрерывная случайная величина, вероятностная мера точки есть нуль.

Отметим, что, хотя точка не является полуоткрытым интервалом, мы имеем право рассматривать вероятностную меру точки, поскольку в классе полуоткрытых интервалов может быть построена бесконечная сходящаяся последовательность, пределом которой является точка, принадлежащая сигма-алгебре Â.

Числовые характеристики

М о м е н т ы. Моменты непрерывных случайных величин определяются так же, как в разд. 1.3.3 были определены моменты дискретных случайных величин, с той разницей, что здесь вместо суммирования будет применено интегрирование. Обозначения моментов оставим прежними.

Начальные моменты порядка k(или k-е начальные моменты):

.

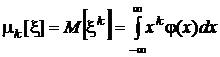Центральные моменты порядка k (или k-е центральные моменты):

.

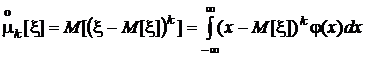В теории вероятностей и математической статистике особую роль играют несколько моментов от первого до четвертого порядка.

Первый начальный момент 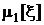или математическое ожидание характеризует положение непрерывной случайной величины на оси. Если прибегнуть к механическим аналогиям, как это было в разд. 1.3.3, математическое ожидание случайной величины – это абсцисса центра тяжести фигуры под кривой плотности распределения.

Эту характеристику находят, как и в разд. 1.3.3, из равенства моментов относительно начала координат: вращающего момента, создаваемого “весом” оси, плотность которой 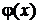зависит от координаты, и момента, который должна создать равнодействующая сила, равная “весу” всей оси, чтобы установилось равенство этих моментов:

.

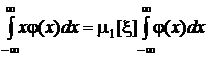Поскольку 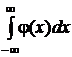=1, окончательно получим выражение для абсциссы центра тяжести, то есть математического ожидания:

.

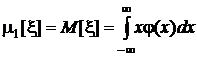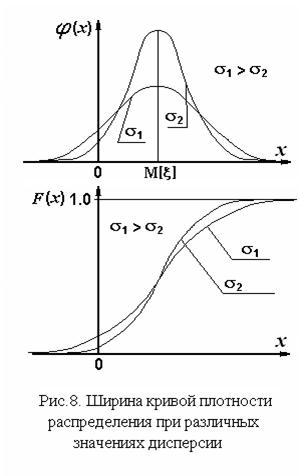
Характеристикой разброса значений случайной величины является дисперсия или второй центральный момент (см. рис. 8):

,

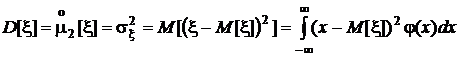который в механической интерпретации есть момент инерции стержня с плотностью 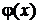относительно центра тяжести (математического ожидания). С увеличением дисперсии кривая плотности распределения расширяется. Площадь под кривой остается постоянной и равна 1.

В левой части этого выражения приведены все возможные обозначения дисперсии. В частности, корень квадратный из дисперсии

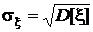
имеет самостоятельное применение и называется среднеквадратическим значением или среднеквадратическим отклонением (сокращенно с.к.о.) случайной величины.

Раскрывая скобки под интегралом в последнем соотношении, найдем полезную связь между вторыми начальным и центральным моментами:

.

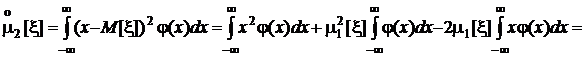
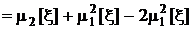Окончательно получим (см. также разд. 1.3.3)

.

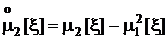Данное соотношение часто применяется при компьютерной обработке результатов измерений (испытаний) в темпе получения данных.

Х а р а к т е р и с т и к и ф о р м ы к р и в о й п л о т н о с т и р а с -п р е д е л е н и я. Одной из характеристик формы кривой плотности распределения, а именно, ширины этой кривой является второй центральный момент, то есть дисперсия.

Другими характеристиками формы являются безразмерные величины, производные от третьего и четвертого центральных моментов, то есть коэффициент асимметрии As (или асимметрия) и коэффициент эксцесса ex(или эксцесс):

, .

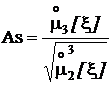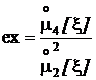Асимметрия – это характеристика степени отклонения от симметричности формы кривой плотности распределения относительно математического ожидания случайной величины. Асимметрия случайных величин с симметричной формой кривой плотности распределения равна нулю. Как видно из выражения для центральных моментов нечетных порядков, эти моменты равны нулю для всех симметричных плотностей, поскольку в этих случаях подынтегральная функция – нечетная.

Эксцесс – это характеристика остроты и степени приближения к оси абсцисс кривой плотности распределения. Эксцесс возрастает при заострении вершины кривой плотности распределения или при уменьшении скорости приближения этой кривой к оси абсцисс на бесконечности.

С п е ц и ф и ч е с к и е т о ч к и к р и в ы х п л о т н о с т и р а с - п р е д е л е н и я и ф у н к ц и и р а с п р е д е л е н и я.

Мода – значение абсциссы 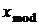, при котором кривая плотности распределения имеет максимум. Мода указывает положение высоковероятной области значений случайной величины, то есть области, в которой вероятностная мера интервала фиксированной ширины максимальна. Это свойство становится очевидным, если вспомнить о том, что вероятностная мера интервала – это площадь под кривой плотности распределения над этим интервалом.

Медиана – значение абсциссы , при котором фигура под кривой плотности распределения делится на две равновеликие части, площади которых равны по 1/2 каждая, а это значит, что .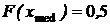

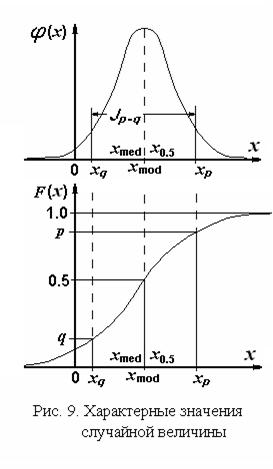
Кривые плотности распределения могут иметь более одного максимума, то есть более одной моды. Тогда такие распределения называются многомодальными. Из многомодальных распределений чаще всего в технических приложениях встречаются двумодальные распределения, которые порождены явлениями типа гистерезиса или сухого трения. На рис. 7 – 9 представлены примеры одномодальных симметричных плотностей распределения. В частности, из рис. 9 видно, что мода 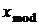, медиана и математическое ожидание таких распределений совпадают:

= = M[x].

Квантиль – значение абсциссы 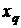, которое является решением уравнения (см. рис. 9) .

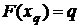Квантиль 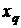называется q-й или q×100-процентной квантилью функции распределения (или плотности распределения, или случайной величины).

В частности, медиана, как следует из ее определения, является 50- процентной квантилью и обозначается, как 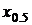или .

На рис. 9 показаны квантили: p×100-процентная квантиль 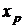, q×100-процентная квантиль 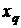и медиана.

Наиболее употребительные квантили:

уже упоминавшаяся медиана = ,

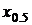квартиль – 25-процентная квантиль,

дециль – 10-процентная квантиль.

Промежуток между квантилям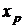и и 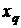, то есть интерквантильный промежуток обозначается 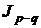и наряду с дисперсией является характеристикой ширины кривой плотности распределения случайной величины.

В технических приложениях интерквантильный промежуток есть характеристика погрешности регулирования, позиционирования или результата измерения. В условиях действия стохастических внешних факторов нормы на эти технические характеристики систем автоматического регулирования, роботов, средств и результатов измерений задаются в виде интервалов с указанием их вероятностной меры, а именно, вероятности того, что указанные погрешности не выйдут за пределы этих норм. Значение вероятности, как правило, задают равным 0.95, а границы интервалов могут быть установлены одним из двух способов: симметрично относительно математического ожидания исследуемой величины или относительно начала координат. Различие между этими вариантами показано на рис. 10. В наших терминах эти интервалы суть не что иное, как интерквантильные промежутки:

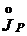– интерквантильный промежуток, симметричный относительно математического ожидания (см. рис. 10 а),

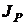– интерквантильный промежуток, симметричный относительно начала координат (см. рис. 10 б).

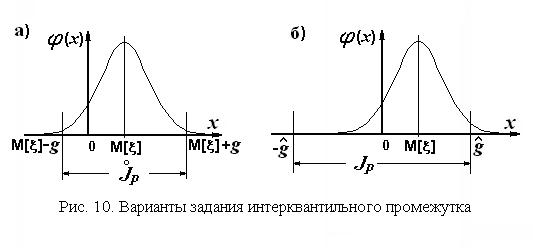
Второй промежуток шире, чем первый. Такая ситуация возникает при назначении норм погрешности технического средства (регулятора, позиционера, средства измерений) при условии, что не устанавливаются раздельные нормы случайной и систематической составляющих этой погрешности.

Если же нормы систематической и случайной составляющих погрешности устанавливаются раздельно (на каждую из них) или если систематическая составляющая исключена путем введения поправки, или если систематическая составляющая погрешности отсутствует, то для нормирования случайной составляющей применяется интерквантильный промежуток 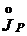, симметричный относительно математического ожидания.