Двумерные дискретные случайные величины

Распределение вероятностей

Будем рассматривать двумерную случайную величину как двумерный случайный вектор

.

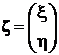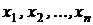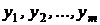Компонентами вектора ζ являются дискретные случайные величины x и h, которые могут принимать значения и соответственно. Реализации вектора ζ будем обозначать вектором z.

При каждом испытании компоненты вектора ζ могут принимать значения 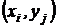с вероятностью совместного осуществления двух событий 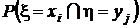. В дальнейшем будем пользоваться упрощенными обозначениями этой вероятности в виде 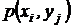или .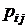

Кроме того, заметим, что события 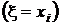образуют полную группу попарно несовместных событий. То же самое можно утверждать и о событиях .

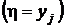Представим совместное распределение вероятностей 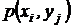в виде таблицы 1.

События 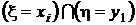, , 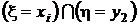..., 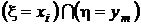не пересекаются, а их объединение есть не что иное, как событие 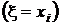. Поэтому, суммируя элементы этой таблицы по строкам, в соответствии с аксиомой аддитивности (см. разд. 1.2.2) получим значения вероятностей 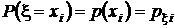. По этой же причине суммирование элементов таблицы по столбцам даст значения вероятностей .

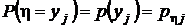Таблица 1

Совместное рaспределение вероятностей дискретного случайного вектора

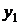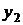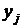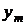h x			. . .		. . .		Маргинальное распределение случайной величины x
			. . .		. . .
			. . .		. . .
. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .
			. . .		. . .
. . .	. . .	. . .	. . .	. . .	. . .	. . .	. . .
			. . .		. . .

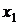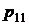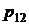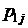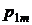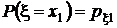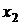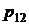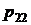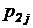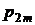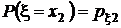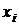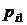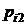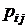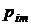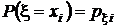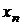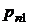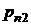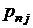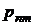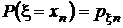Тот же результат мы получим, если определим условные вероятности

,

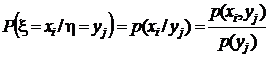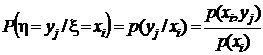
и поскольку события 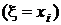и 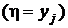образуют полные группы попарно несовместных событий, применим формулу полной вероятности

,

.

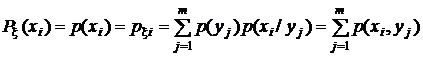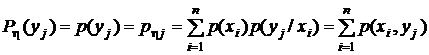Сумма всех вероятностей .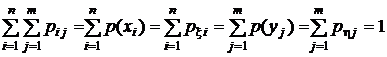

Мы получили маргинальные (частные) распределения случайных компонент x и h(см. также разд. 1.3.1):

;.

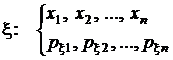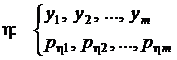Признак независимости случайных компонент вектора ζ: случайные компоненты x и hвектора ζ независимы тогда и только тогда, когда их совместное распределение вероятностей может быть представлено как произведение маргинальных (частных) распределений (см. также разд. 1.2.3): .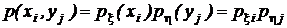

Числовые характеристики

Числовые характеристики, а именно моменты отдельных составляющих вектора ζ определяются через маргинальные (частные) распределения точно так же, как для одномерной (скалярной) дискретной случайной величины:

начальные моменты k-го порядка

, ,

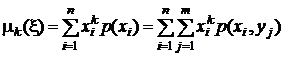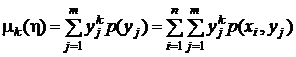в частности, математические ожидания

, ;

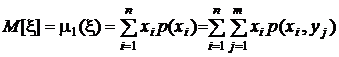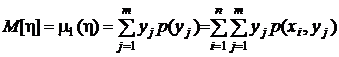центральные моменты k-го порядка

,

,

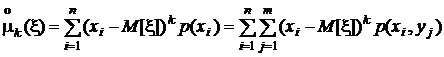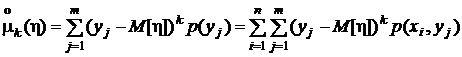в частности, дисперсии

,

.

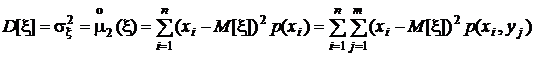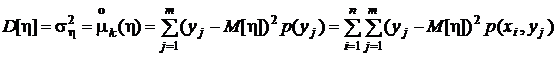Для составляющих случайного вектора определены смешанные моменты:

начальные моменты порядка k, r

;

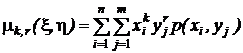центральные моменты порядка k, r

.

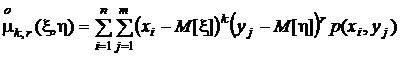Особое значение для дальнейшего имеет центральный смешанный момент порядка (1, 1),который называется корреляционным моментом или ковариацией:

.

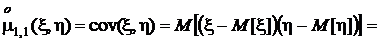
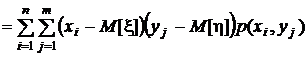Для того чтобы установить соотношение между центральным и начальным смешанными моментами раскроем скобки в последнем выражении и выполним несложные преобразования:

.

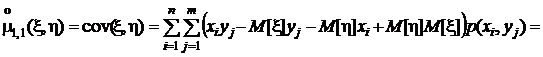
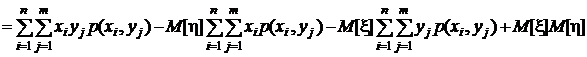Окончательно получим .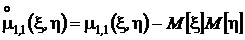

Если x и h независимы, то

.

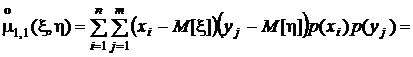
Но, как было установлено в разд. 1.3.3, 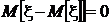и 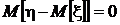, поэтому центральный смешанный момент 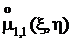независимых случайных величин равен нулю. Однако из того, что 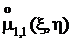=0, независимость случайных величин x и h,вообще говоря,не следует. О случайных величинах, корреляционный момент которых равен нулю, говорят, что они не коррелированы. Для оценки степени коррелированности случайных величин в приложениях удобнее использовать безразмерный коэффициент корреляции 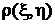. Его значение не зависит от масштаба, в котором выражены значения случайных величин:

.

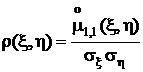С целью определения диапазона значений коэффициента корреляции рассмотрим крайний случай взаимно однозначной зависимости между x и h,а именно допустим, что h = ax + b. Другой крайний случай, а именно независимость x и h,рассмотрен ранее в настоящем разделе.

Из предположенной линейной зависимости следует (см. также разд. 1.3.4):

, ,

.

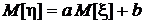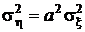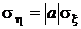
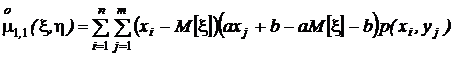После простых преобразований получим

,

.

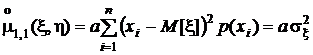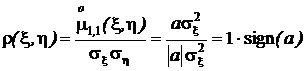Таким образом мы установили, что коэффициент корреляции не превышает единицу по абсолютной величине: .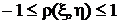

Математическое ожидание случайного вектора – вектор, составляющие (компоненты) которого суть математические ожидания соответствующих компонент:

.

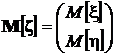Дисперсии компонент случайного вектора ζ и их ковариации объединяют в ковариационную матрицу следующим образом:

.

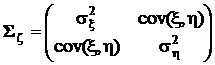В теории вероятностей часто используется корреляционная матрица, которая получается из ковариационной матрицы путем деления ее элементов на произведение среднеквадратических значений:

.

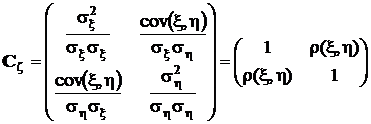Эти матрицы симметричны и неотрицательно определены. Если компоненты случайного вектора независимы или хотя бы не коррелированы, матрицы 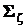и 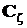диагональны.

Математическое определение ковариационной матрицы:

,

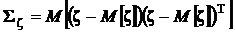где Т – символ транспонирования.

Раскроем это выражение.

.

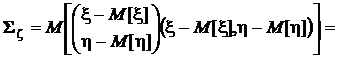
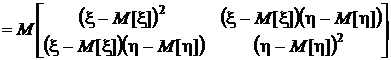Математическое ожидание случайной матрицы есть матрица, элементы которой суть математические ожидания:

=

,

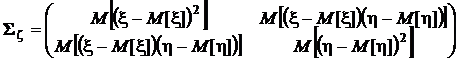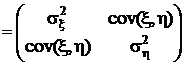с чем мы уже ознакомились в настоящем разделе.

1.4.3. Линейное преобразование случайного вектора.

Числовые характеристики

Общий вид линейного преобразования случайного вектора есть умножение его на матрицу и добавление произвольного неслучайного вектора:

.

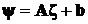Раскроем это преобразование:

.

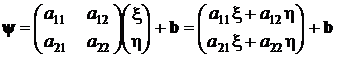Вычислим вначале математическое ожидание от первой составляющей первого из векторов:

.

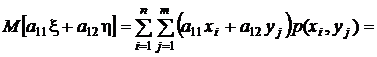
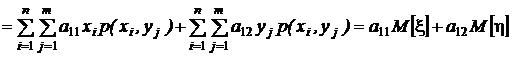Точно так же

.

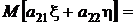
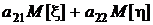Поэтому

.

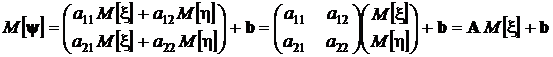В соответствии с математическим определением ковариационной матрицы

.

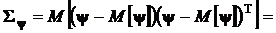
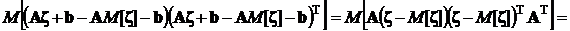
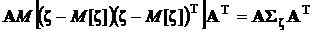Таким образом, если случайный вектор ζ претерпевает преобразование 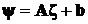, то математическое ожидание и ковариационная матрица результата такого преобразования вычисляются по формулам

, .

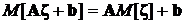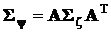Мы снова убеждаемся в том, что ковариационная матрица не зависит от смещения, которое задается вектором b.

Рассмотрим в качестве примера важный частный случай. Пусть матрица Aимеет вид 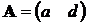, а вектор 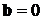. Тогда y – скаляр (y = 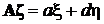), и ковариационная матрица 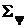также вырождается в скаляр, а именно в дисперсию, которую будем обозначать 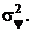Най­дем математическое ожидание и дисперсию случайной величины y,пользуясь полученными формулами.

,

.

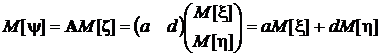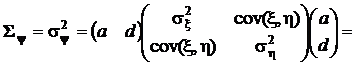
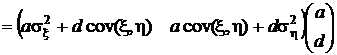Перемножив эти два вектора, окончательно получим

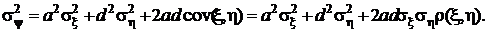
Частные случаи:

случайные величины x и h независимы или хотя бы не коррелированы, тогда ;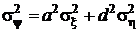

коэффициенты a = b = 1, то есть случайная величина y есть сумма двух не коррелированных случайных величин x и h, тогда 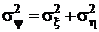, то есть дисперсия суммы не коррелированных случайных величин равна сумме дисперсий слагаемых.