Случайные события, виды случайных событий

основные понятия и определения

Событие называется случайным, если в результате испытаний при осуществлении некоторой совокупности условий S оно может произойти или не произойти. Под “испытанием” может пониматься проявление какого-либо природного явления или спланированный исследователем эксперимент над рукотворным или природным объектом.

Элементарный исход – результат одного испытания в условиях S.

Характеризационное свойство (признак) элементарных исходов: элементарные исходы взаимно исключают друг друга, и в результате каждого испытания может произойти только один из элементарных исходов. Обозначение элементарного исхода .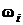

Примеры элементарных исходов:

результат бросания монеты на идеальную плоскость;

результат бросания игральной кости и выпадение на верхней грани какого-либо числа;

результат одновременного бросания нескольких игральных костей и выпадение на верхних гранях всех костей определенной комбинации цифр.

Все элементарные исходы, возможные при условиях S, образуют пространство элементарных исходов 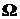: 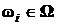, i=1, 2, ... .Каждый элементарный исход влечет за собой появление какого-либо события. В общем случае событие A может произойти при появлении элементарных исходов, принадлежащих некоторому подмножеству 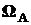пространства 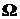, 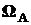Ì .

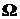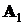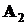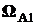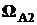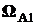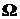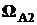Пусть в целях некоторого исследования сформулированы условия S и события и , которые могут произойти в результате испытаний при появлении элементарных исходов, принадлежащих подмножествам и , Ì , Ì 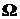.Запишем это сопоставление событий и элементарных исходов в виде

, .

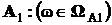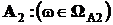Пусть в этих же условиях определено событие B следующим образом: “Событие B происходит или при осуществлении события 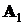, или при осуществлении события 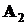”. При такой формулировке говорят, что событие B является объединением событий 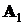и 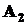и записывают: 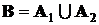. В этом случае подмножество элементарных исходов, влекущих за собой событие B, есть объединение подмножеств 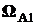и :

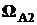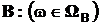, где .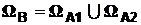

Если в этих же условиях принято, что событие B происходит, когда осуществляются события 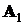, и 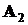, то говорят, что событие B есть пересечение событи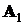й и 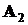, и записывают этот факт в виде 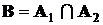, причем и в этом случа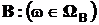е , где .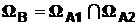

В дальнейшем для упрощения обозначений подмножество элементарных исходов 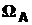будем считать событием A,так же его обозначать, и вместо запис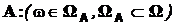и или 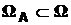будем писать A Ì 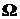. Такое отождествление удобно использовать также для наглядного представления событий (см. рис. 1 – 3).

Обычно пространство 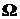представляют внутренностью прямоугольника, каждая точка которой есть представление элементарного события. В этом случае совокупность элементарных событи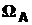й или 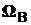образует некоторые замкнутые фигуры внутри прямоугольника. Поскольку эти элементарные события отождествляются с порождаемыми ими событиями A и B взаимно однозначно, то в целях упрощения эти замкнутые фигуры обозначаются A и B соответственно.

Случайные события могут образовывать классы событий, о чем пойдет речь ниже в разд. 1.2.2.

Виды случайных событий:

достоверное событие Т: (wÎ 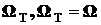) – событие, которое непременно происходит при появлении любого элементарного исхода в условиях S;

невозможное событие Æ – событие, которое не может произойти ни при одном элементарном исходе из пространства 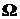при условиях S;

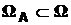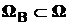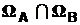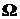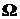события A и B несовместны, если появление одного из них исключает появление другого из них, для несовместных событий можно записать: , , – пустое множество, или в упрощенных обозначениях : A Î , B Î , A 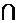B = Æ;

события A и Bпротивоположны, если они несовместны и A 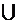B = Т, в этом случае пользуются обозначениями B = 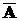или A = ;

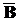события 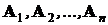образуют полную группу попарно несовмест­ных событий, если при условиях S осуществляется только одно из этих событий и

, , .

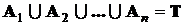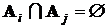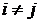Вероятность событий

Вероятность (осуществления) события – числовая характеристика возможности события при условиях S. Если 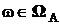, то вероятность события А есть вероятностная мера множества 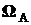, обозначается P(A).

Приведем математические определения вероятности события.

К л а с с и ч е с к о е о п р е д е л е н и е:

P(A) есть отношение количества случаев, благоприятствующих появлению события A, к общему числу испытаний.

Ч а с т о т н о е о п р е д е л е н и е:

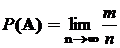
где n – общее число выполненных испытаний, m – количество случаев появления события A при этих испытаниях.

С о в р е м е н н а я а к с и о м а т и к а (А. Н. Колмогоров):

P(A) – неотрицательная монотонная счетно-аддитивная мера возможности случайного события, такая, что P(T) = 1.

Пояснения к этой аксиоматике:

неотрицательность: P(A) ³0;

монотонность: если A Ì B тоP(A) £P(B), то есть, если при наступлении события A обязательно наступает событие B, но обратное необязательно, то P(A) £P(B);

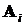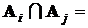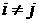счетная аддитивность: если условия S определены, события попарно несовместны, то есть Æ, , то

.

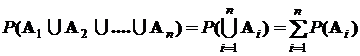В современной теории вероятностная мера определяется на классах событий. Классы событий образуются таким образом, чтобы они давали возможность определить вероятностную меру вначале на простейших событиях, а затем распространить ее на события любой сложности. Для этого класс событий должен содержать в себе не только сходящиеся в этом классе последовательности событий, но также их пределы. Обозначим класс событий Â.

Если в условиях Sсобытия 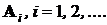принадлежат классу событий Â, и счетное объединение и счетное пересечение этих событий также принадлежит этому классу, то есть

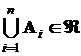и ,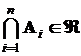

то этот класс событий называется алгеброй событий.

Если в этих же условиях 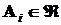, 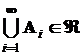и 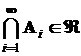, то такой класс событий называется сигма-алгеброй (s-алгеброй).

П р и м е р и з п л а н и м е т р и и. Класс всех многоугольников образует алгебру многоугольников, поскольку пересечение счетного количества многоугольников есть также многоугольник. Дополнение этого класса бесконечными пересечениями и объединениями многоугольников, что мы делали для определения меры (площади) круга, привело к образованию сигма-алгебры, и это позволило с помощью предельного перехода распространить меру (площадь) на геометрические фигуры, которые не являются многоугольниками, но суть пределы, к которым стремятся бесконечные сходящиеся последовательности многоугольников при их объединении и пересечении.

В итоге в соответствии с современной аксиоматикой теории вероятностей говорят, что случайные события и вероятностная мера этих событий определены тройкой: (W, Â,P), где фигурируют введенные обозначения пространства элементарных событий, сигма-алгебры событий и вероятностной меры на них [4].

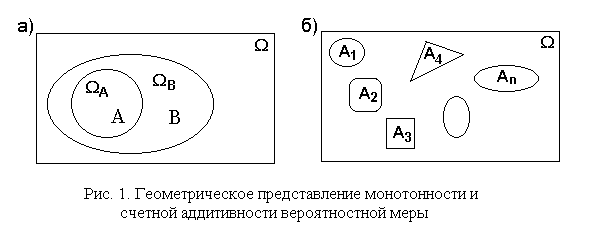
Для иллюстрации введенных понятий и свойств вероятностной меры, как было указано ранее, прибегают к геометрическому представлению событий в виде замкнутых фигур внутри прямоугольника, который представляет собой пространство элементарных событий W. Вероятностная мера событий отождествляется с площадью соответствующих фигур с учетом того, что вероятностная мера всего прямоугольника равна единице.

Это представление событий и вероятностей показано на рис. 1, который иллюстрирует свойства монотонности (рис. 1, а) и счетной аддитивности (рис. 1, б) вероятностной меры.

Из аксиоматики Колмогорова следует:

а) ;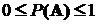

б) 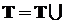Æ,откуда следует: P(T)=1=P(T)+P(Æ)=1+P(Æ),

и, наконец, P(Æ)=0;

в) AÎW, B ÎW, AиBпротивоположны, то есть A 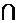B = Æ, A 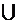B = Т;

тогда P(A 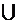B) =P(A)+P(B) =P(T) =1,откуда 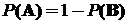, то есть

, ;

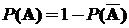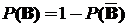г) пусть AÎW, B ÎWисобытия пересекаются, то есть 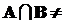Æ.

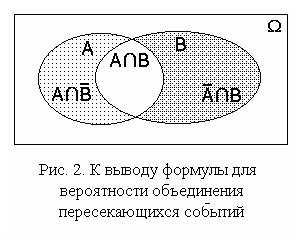В этом случае вероятность объединения событий не равна сумме вероятностей. Для вывода формулы представим объединение пересекающихся событий A и B в виде объединения трех непересекающихся событий (рис. 2): .

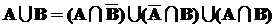Точно так же представим события

A и B: , .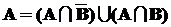

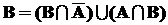К этим выражениям можно применить аксиому счетной аддитивности вероятностной меры:

,

, ,

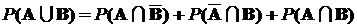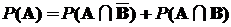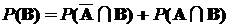откуда следует, что 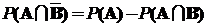и .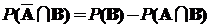

Подставляя эти два выражения в первое, окончательно получим

=

= .

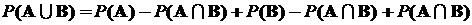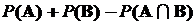Очевидно, что в случаях, когда события несовместны, то есть не пересекаются,

,

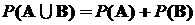а в общем случае всегда .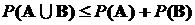

Условная вероятность

Пусть, как всегда, A 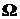Ì , B Ì 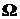и сформулированы условия S.

Условная вероятность есть вероятность осуществления одного из событий при условии, что другое событие состоялось. Обозначение условных вероятностей:

P(B/A) – условная вероятность события B при условии осуществления события A;

P(A/B) – условная вероятность события A при условии осуществления события B.

Найдем условную вероятность, например, P(B/A)с помощью классического определения вероятности по разд. 1.2.2. Для этого необходимо знать общее количество n предполагаемых испытаний, в результате которых могут осуществиться события A, B, A 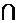B.

Общее количество исходов, при которых возможна реализация условного событияB/A, определяется исключительно числом появления события A, поскольку если оно не осуществится, то не осуществится и условное событиеB/A.Пусть m – число исходов, благоприятствующих появлению события A. Понятно, что в общем случае .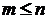

В результате предполагаемых испытаний событие B может появиться и без появления события A, но условное событие B/A осуществляется только при совместном появлении событий A и B. В связи с этим число случаев, благоприятствующих появлению событияA 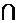B,равно количеству случаев, благоприятствующих появлению события B/Aили события A/B.Обозначим это количество s.

Тогда в соответствии с классическим определением вероятности

P(В/А)= ,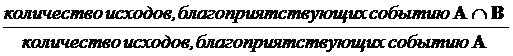

то есть

.

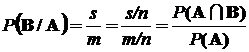Таким образом, условная вероятность P(В/А) определяется, как

.

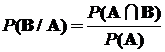Точно так же

.

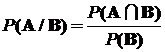Из полученных выражений следует, что

.

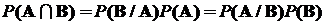События A и B независимы, когда P(B/A)=P(B) и P(A/B)=P(A).

Отсюда следует формулировка признака независимости случайных событий:

события A и Bнезависимы тогда и только тогда, когда

P(A 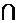B)=P(A)P(B).

В самом деле, при таком соотношении

.

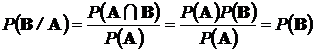Если A и Bсвязаны взаимно однозначно, тоm=s, а потому

P(A 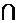B)=P(A)=P(B),P(B/A)=1,P(A/B)=1.

1.2.3.1. Формула полной вероятности

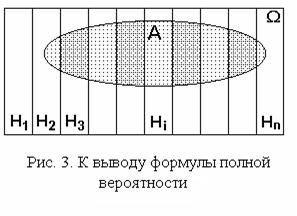Пусть при условиях S в возможно событие A. Кроме того в определена полная группа попарно непересекающихся событий 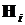, i=1, 2, ..., n, то есть

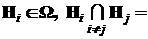Æ, .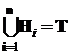

Данная ситуация представлена на рис. 3. Из предъявленных соотношений следует, что

.

Воспользовавшись аксиомой Колмогорова о счетной аддитивности вероятностной меры и математическим определением условных вероятностей, получим:

.

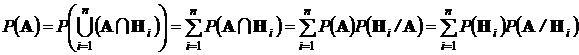Таким образом получена формула полной вероятности:

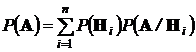
в которой события 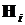именуются гипотезами.

1.2.3.2. Формула Байеса

Воспользовавшись формулой условной вероятности и формулой полной вероятности, получим ценную для многочисленных приложений формулу Байеса:

.

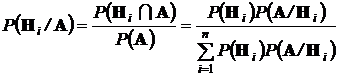Формула Байеса эффективно используется при исследованиях природных явлений, при исследованиях и испытаниях рукотворных объектов в условиях неопределенности математической модели исследуемых объектов и действия мешающих случайных воздействий. В этих условиях события, происходящие при исследованиях, неоднозначно связаны со свойствами и параметрами объектов.

Пусть 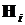– гипотезы (предположения) исследователя о свойствах или параметрах исследуемого объекта, рукотворного или природного. Эти гипотезы могут иметь одинаковый или различный приоритет, который выражается путем задания значений вероятностей 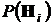. Эти вероятности в данной ситуации суть априорные вероятности гипотез .

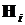В результате эксперимента или исследования событиеA происходит с той или иной вероятностью. Это событие исследователь фиксирует, и по нему он должен вынести суждение об оправданности того или иного априорного предположения (гипотезы). В силу действия случайных факторов и неопределенности математической модели объекта однозначные причинно-следственные связи между предположениями (гипотезами) исследователя и результатами испытаний размыты. После выполнения эксперимента (испытания) фиксируется событие A. В этой ситуации можно оценить условные вероятности 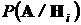возможности реализации события A при справедливости каждой из гипотез. Таким образом после эксперимента правая часть формулы Байеса может быть рассчитана, и формула Байеса дает возможность оценить апостериорную вероятность той или иной гипотезы при условии, что результатом эксперимента оказалось событие A.

Естественно принять в качестве наиболее правдоподобного то предположение (гипотезу), апостериорная вероятность которого окажется наибольшей. Такое правило принятия решения, которое основано на применении формулы Байеса, называется байесовским. Этой же формулой порожден принцип максимума апостериорной вероятности, который часто и эффективно используется в теории и практике систем автоматического регулирования, при математической обработке результатов измерений, при идентификации объектов.

Наиболее широкое применение байесовский принцип максимума апостериорной информации находит в системах передачи информации по каналам связи, в которых велика вероятность искажения передаваемых символов и сообщений. Обычно это цифровые каналы. В них на передающей стороне применяется избыточное кодирование сообщений, а на приемной стороне устанавливается байесовский декодер, реализующий указанный байесовский принцип в реальном времени.