Последовательность независимых испытаний
П. 1. Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 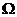 элементарных событий.
элементарных событий.
Определение.Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность n независимых испытаний, под которой будем понимать дискретное новое пространство 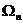 элементарных исходов, состоящее из точек (е1, е2, …,еs,…,еn), где еs – произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из k исходов:
элементарных исходов, состоящее из точек (е1, е2, …,еs,…,еn), где еs – произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из k исходов: 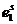 или
или 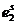 или ….
или …. 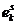 .
.
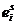 – i –тый исход в s-том испытании, где i = 1,2,…,k; s = 1, 2,…, n.
– i –тый исход в s-том испытании, где i = 1,2,…,k; s = 1, 2,…, n.
Пример. Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 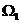 состоит из шести точек:
состоит из шести точек: 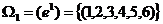 , т.е. шесть исходов. Если провести три испытания, то пространство
, т.е. шесть исходов. Если провести три испытания, то пространство 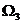 состоит из 216 точек.
состоит из 216 точек.
Обычно исходы обозначали большими заглавными буквами. Переобозначим!
Пусть происходит n независимых испытаний: 1, 2,…, s,…, n. В кажlом испытании может произойти k исходов: 1-ый, 2, 3,…, i,…, k-ый.
Обозначим событие 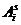 – i –тый исход в s-том испытании, где i = 1,2,…,k; s = 1, 2,…, n.
– i –тый исход в s-том испытании, где i = 1,2,…,k; s = 1, 2,…, n.
Эти k исходов – несовместные случайные события. Тогда для s-ого испытания можем записать: 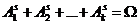 , причем
, причем 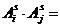 Ø.
Ø.
Обозначим вероятность i –ого исхода при s-том испытании через 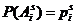 .
.
Пусть при первом испытании произошло событие под номером i1, при 2-ом – событие под номером i2, …, при n-ом – событие под номером in. Результат сразу n испытаний – событие, которое обозначим через произведение событий 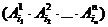 – цепочкарезультатов отдельных испытаний.
– цепочкарезультатов отдельных испытаний. 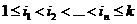 . Данное событие – цепочка состоит из всех точек (е1, е2, …,еs,…еn) пространства
. Данное событие – цепочка состоит из всех точек (е1, е2, …,еs,…еn) пространства 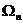 , для которых е1
, для которых е1 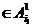 , е2
, е2 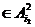 , …, еn
, …, еn 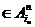 .
.
Испытания – независимые, следовательно, по теореме 4, имеет место равенство:
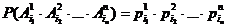
В случае, когда вероятности событий 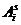 не зависят от номера испытаний,
не зависят от номера испытаний, 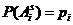 ,
, 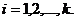
В силу несовместности и единственной возможности исходов, очевидно, что 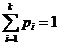 , так как
, так как 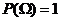 .
.
Теорема.Если данныеn испытаний независимы, то любые m из них также независимы.
Теорема. Для того, чтобы n испытаний были независимы, необходимо и достаточно выполнения условия:
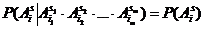 ,
,
Для любой группы чисел s, s1, s2,…,sm (1 < s, s1, s2,…,sm < n) и любых m, i, i1, i2,…, im, 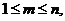
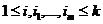 .
.
П. 2. Формулы Бернулли.
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (k = 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – p, в каждом испытании.
Определение. Независимые испытания при двух исходах называются испытаниями Бернулли.
Рассмотрим задачу.Определить вероятность того, что в результате проведения n независимых испытаний некоторое событие А – успех (У) наступит ровно m раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью Р(А) = Р(У) = р.
Решение.
Искомую вероятность обозначим Pm,n или Pn(m).
Событие А в данных испытаниях может появиться ровно m раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные (n–m) наступает противоположное событие 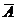 – неудача (Н), вероятность которого Р(
– неудача (Н), вероятность которого Р( 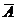 ) = Р(Н) = q, (q = 1 – p).
) = Р(Н) = q, (q = 1 – p).
Сначала найдем вероятность того, что события У наступают при определенных m испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида:
УУУННУНН…УН(где У – m штук, Н – (n-m) штук).
По условию данные события – независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
Р(УУУННУНН…УН) = Р(У)Р(У)Р(У)Р(Н)Р(Н)….Р(У)Р(Н) = рmqn-m.
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из n мест m мест для успехов. Это можно сделать 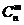 способами. Следовательно,
способами. Следовательно,
Pn(m) = 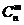 рmqn-m
рmqn-m
В данной задаче мы доказали теорему Бернулли:
Теорема Бернулли.Если m – число успехов в n независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно m раз, находится по формуле: Pn(m) = 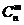 рmqn-m, которая называется формулой Бернулли.
рmqn-m, которая называется формулой Бернулли.
Следствие. 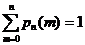 , так как события, состоящие в различном числе появления события А в серии n испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так:
, так как события, состоящие в различном числе появления события А в серии n испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так: 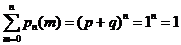 .
.
Пример.
Пусть монета брошена 5 раз.Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
Два исхода (k = 2: орел, решка) при 5 независимых испытаниях (n = 5)– схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка) 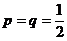 . Количество успехов: m = 3.
. Количество успехов: m = 3.
По формуле Бернулли Pn(m) = 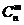 рmqn-m найдем искомую вероятность:
рmqn-m найдем искомую вероятность:
P5(3) = 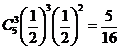 .
.
Замечания.
Замечание 1.Вероятность Pn(m) равна коэффициенту при xm в разложении бинома (q+px)n по степеням x. В силу этого свойства совокупность вероятностей Pn(m) называют биномиальнымзаконом распределения вероятностей. (будем изучать позднее)
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из n независимых испытаний имеет k взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из k несовместных событий: 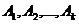 с вероятностями
с вероятностями 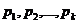 , не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих n испытаний m1 раз события А1, m2 раза события А2,…,mk раз события Аk. (m1 + m2 + …+ mk = m). Данная вероятность находится по формуле:
, не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих n испытаний m1 раз события А1, m2 раза события А2,…,mk раз события Аk. (m1 + m2 + …+ mk = m). Данная вероятность находится по формуле:
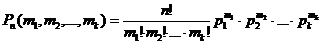 .
.
Эта совокупность вероятностей является коэффициентом при 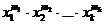 в разложении полинома
в разложении полинома 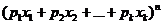 по степеням x. Поэтому эту схему называют полиномиальной.
по степеням x. Поэтому эту схему называют полиномиальной.
Например.При n подбрасываниях игральной кости получается полиномиальная схема с шестью исходами ( k = 6) и вероятностями 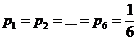 .
.
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами (k = 2) и вероятностями успеха 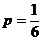 и неудачи
и неудачи 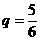 .
.
Замечание 3.При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида:
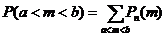 .
.
Например, вероятность того, что событие наступит а) менее k раз, b) более k раз, c) не менее k раз, d) не более k раз находятся соответственно по формулам:
а) 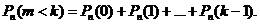
b) 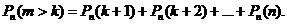
с) 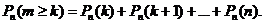
d) 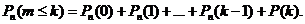
В некоторых случаях удобнее перейти к противоположному событию, например, 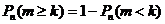 .
.
Пример.
Пусть монета брошена 5 раз.Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода (k = 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи 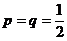 .
.
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
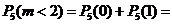 (вероятности найдем по формуле Бернулли) =
(вероятности найдем по формуле Бернулли) = 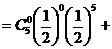
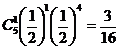 .
.
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
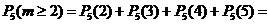 (удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) =
(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) = 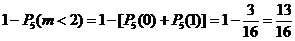 .
.
Замечание 4.В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях p или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
