Лекция 19. Последовательность независимых испытаний

Модуль 3.

Лекция 19. Последовательность независимых испытаний

Раздел 19.1. Схема Бернулли

Повторные независимые испытания. Схема Бернулли.

Формула Бернулли

Раздел 19.2. Предельные теоремы для схемы Бернулли:

Локальная теорема Муавра-Лапласа. Функция Гаусса

Интегральная теорема Муавра-Лапласа. Функция Лапласа

Теорема Пуассона

Программные положения

В лекции речь идет об анализе результата повторных испытаний – последовательного проведения n раз одного и того же опыта или одновременного проведения n одинаковых опытов. Речь идет о классической модельной схеме эксперимента с повторением независимых испытаний с двумя возможными исходами – схеме Бернулли. Рассматриваются формула Бернулли и приближенные формулы для вычисления числа успехов

Методические рекомендации

Перед чтением лекции повторите определение независимых событий.

Уделите внимание тому, как будет выглядеть пространство элементарных событий для схемы Бернулли для схемы из n испытаний (при конкретных n).

Докажите формулу Бернулли и укажите, какие ограничения накладывает количество испытаний. Обратите внимание на функции Гаусса и Лапласа, их свойства и графики

Вопросы для самоконтроля

1. Что такое независимые испытания?
2. Что такое Схема Бернулли?
3. Докажите формулу Бернулли
4. Что позволяют вычислить предельные теоремы для схемы Бернулли? Каковы причины их применения?
5. Сформулируйте Локальную теорему Муавра-Лапласа. Что такое функция Гаусса? Каковы ее свойства?
6. Сформулируйте Интегральную теорему Муавра-Лапласа. Каковы условия ее применения?
7. Что такое функция Лапласа? Каковы ее свойства?
8. Сформулируйте теорему Пуассона. Каковы условия ее применения?
9. Игральная кость подбрасывается 1000 раз. Какова вероятность того, что число, не меньшее 5, выпадет а)ровно 300 раз? б) число раз в промежутке от 300 до 400?
10. Вероятность попасть в двигающуюся мишень у начинающего стрелка 0,01. Он делает 200 выстрелов. Какова вероятность того, что он а) не попадет ни разу б) попадет не более 2 раз?

Литература по теме

А.Н.Бородин «Элементарный курс теории вероятностей и математической статистики» Часть I, пп.9-10

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 13, п.13.7

Б.В.Гнеденко «Курс теории вероятностей» Глава 2

Теория вероятностей под ред. В.С.Зарубина, А.П.Крищенко (серия «Математика в техническом университете», выпуск XVI, МГТУ им.Баумана) Глава 3

Пример 19.1.3.

Вероятность выигрыша на один лотерейный билет равна 0,01. Определим, сколько билетов нужно купить, чтобы вероятность хотя бы одного выигрыша в лотерее была не менее заданного значения Р_з = 0,9.

Пусть куплено n билетов. Предположим, что общее число билетов, разыгрывающихся в лотерее велико (во много раз больше купленных билетов). При этом можно считать, что каждый билет выигрывает независимо от остальных с вероятностью р = 0,01. Тогда вероятность получить к выигрышных билетов можно определить, используя формулу Бернулли. В частности, имеем при q = 1 — р:

Р{к ≥ 1} = 1 - qⁿ = 1 – (1 - р)ⁿ ≥ Р_з,

откуда получаем

n ≥ ln (1 – P) / ln (1 – p) = ln 0,1 / ln 0,99 ≈ 230

Таким образом, нужно купить не менее 230 лотерейных билетов.

По формуле Бернулли можно подсчитать вероятности всех возможных частот: x=0,1,2,3,4,5.

Формула Бернулли при заданных числах p и n позволяет рассчитывать вероятность любой частоты x (0 £ x £ n). Возникает естественный вопрос: какой частоте будет соответствовать наибольшая вероятность?

Предположим, что такая частота существует, и попытаемся ее определить из условия, что вероятность этой частоты не меньше вероятности "предыдущей" и "последующей" частот:

P_n(x) ³ P_n (x-1);

P_n(x) ³ P_n (x+1)

Первое неравенство представляется в виде:

,

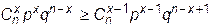что эквивалентно 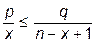или 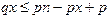. Отсюда следует:

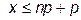
Решая второе неравенство, получим

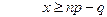
Таким образом, частота, имеющая наибольшую вероятность (чем вероятнейшая частота), определяется двойным неравенством

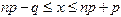
Если np + p – целое число (тогда и np – q – целое число), то две частоты: x=np – q и x=np + p обладают наибольшей вероятностью. Например, при 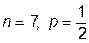, наивероятнейшие частоты: x = 3; x = 4.

Теорема Пуассона.

Асимптотическое представление P_n (x) через j(х) тем хуже, чем больше р отличается от ½ , а для случая p=0, q=1 вообще неприменимо. Однако большой круг задач связан именно с отысканием P_n (x) именно при малых значениях р.Для того, чтобы в этом случае теорема Муавра-Лапласа дала небольшую погрешность необходимо очень большое n, Поэтому требуется специальная формула, предназначенная специально для малых р, которая и приводится в теореме Пуассона:

Если

1) Число испытаний n велико

2) Мы интересуемся вероятностью P_n (x) числа успехов х в серии из n испытаний

3) р уменьшается с ростом n, т.е λ = np – константа(постоянная), т.е, рассматривается случай редких успехов.

Тогда выполняется

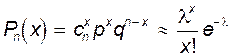
Замечание 19.2.3. Для указанной величины P_n (x) – функции Пуассона - также существуют таблицы.

Пример 19.2.3. Вероятность искажения одного символа при передаче сообщения по линии связи равна 0,001. Сообщение считают принятым, если в нем отсутствуют искажения. Найти вероятность того, что будет принято сообщение, состоящее из 20 слов по 100 символов каждое.

Предлагаемое сообщение содержит 2000 символов. Предполагая, что символы искажаются независимо, получаем схему Бернулли, в которой n=2000, p=0,001, x=0. λ = np=2. Тогда Р ₂₀₀₀(0) = 0,13534 (0! = 1)

Пример 19.2.4. Вероятность попадания в цель при каждом выстреле 0,001. Найти вероятность попадания в цель двумя и более выстрелами, если производится 5000 выстрелов.

Искомая вероятность равна 1 - Р ₅₀₀₀(0) - Р ₅₀₀₀(1) »1 – е^-5 – 5е^-5 » 0,9596

Модуль 3.

Лекция 19. Последовательность независимых испытаний

Раздел 19.1. Схема Бернулли

Повторные независимые испытания. Схема Бернулли.

Формула Бернулли

Раздел 19.2. Предельные теоремы для схемы Бернулли:

Локальная теорема Муавра-Лапласа. Функция Гаусса

Интегральная теорема Муавра-Лапласа. Функция Лапласа

Теорема Пуассона

Программные положения

В лекции речь идет об анализе результата повторных испытаний – последовательного проведения n раз одного и того же опыта или одновременного проведения n одинаковых опытов. Речь идет о классической модельной схеме эксперимента с повторением независимых испытаний с двумя возможными исходами – схеме Бернулли. Рассматриваются формула Бернулли и приближенные формулы для вычисления числа успехов

Методические рекомендации

Перед чтением лекции повторите определение независимых событий.

Уделите внимание тому, как будет выглядеть пространство элементарных событий для схемы Бернулли для схемы из n испытаний (при конкретных n).

Докажите формулу Бернулли и укажите, какие ограничения накладывает количество испытаний. Обратите внимание на функции Гаусса и Лапласа, их свойства и графики

Вопросы для самоконтроля

1. Что такое независимые испытания?
2. Что такое Схема Бернулли?
3. Докажите формулу Бернулли
4. Что позволяют вычислить предельные теоремы для схемы Бернулли? Каковы причины их применения?
5. Сформулируйте Локальную теорему Муавра-Лапласа. Что такое функция Гаусса? Каковы ее свойства?
6. Сформулируйте Интегральную теорему Муавра-Лапласа. Каковы условия ее применения?
7. Что такое функция Лапласа? Каковы ее свойства?
8. Сформулируйте теорему Пуассона. Каковы условия ее применения?
9. Игральная кость подбрасывается 1000 раз. Какова вероятность того, что число, не меньшее 5, выпадет а)ровно 300 раз? б) число раз в промежутке от 300 до 400?
10. Вероятность попасть в двигающуюся мишень у начинающего стрелка 0,01. Он делает 200 выстрелов. Какова вероятность того, что он а) не попадет ни разу б) попадет не более 2 раз?

Литература по теме

А.Н.Бородин «Элементарный курс теории вероятностей и математической статистики» Часть I, пп.9-10

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 13, п.13.7

Б.В.Гнеденко «Курс теории вероятностей» Глава 2

Теория вероятностей под ред. В.С.Зарубина, А.П.Крищенко (серия «Математика в техническом университете», выпуск XVI, МГТУ им.Баумана) Глава 3