Раздел 3. Последовательность независимых испытаний.

Пусть проводится серия из n испытаний, в каждом из которых событие А может наступить с одной и той же вероятностью p или не наступить с вероятностью q=1-p, независимо от номера испытания и результата предыдущего опыта. Такие серии опытов называются последовательностью независимых испытаний или схемой Бернулли. В связи со схемой Бернулли рассматриваются такие задачи: 1) найти вероятность того, что в серии из n испытаний событие А наступит ровно k раз: 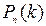; 2) найти вероятность того, что в серии из n испытаний событие А наступит не менее чем 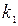раз и не более, чем 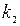раза:

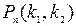
Указанные вероятности находят по формуле Бернулли:

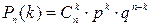
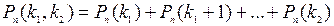
Если число n велико, а p не слишком мало, то для вычисления вероятности можно воспользоваться приближенными (асимптотическими) формулами Муавра-Лапласа (локальная теорема Муавра-Лапласа; интегральная теорема Муавра-Лапласа).

Локальная теорема Муавра – Лапласа:

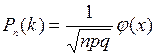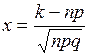, где и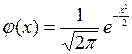

Интегральная теорема Муавра – Лапласа:

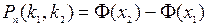, где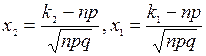

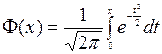
Функции j(´) и Ф(х) табулированы, то есть таблицы значений этих функций приведены в каждом учебнике по теории вероятностей. Можно указать некоторые свойства этих функций: j(-x)=j(x); Ф(-х)=-Ф(х); Ф(0)=0; Ф(х) ® 0,5 при х ® ¥.

Если число испытаний n велико, а вероятность появления события А в каждом испытании мала, то для вычисления вероятности появления k раз события А в серии из n испытаний можно воспользоваться формулой Пуассона

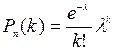, где l=n×p.

Число 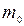успехов, при котором достигается наибольшая из возможных вероятностей, называется наивероятнейшим числом успехов. Оно определяется как целое число на промежутке np – q £ m £ np+p.

Пример 1. По некоторой цели произведено четыре независимых выстрела. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что при четырех выстрелах было ровно одно попадание, и определить наивероятнейшее число попаданий.

Решение. Вероятность попадания при одном выстреле равна p=0,6, а вероятность промаха q = 1-p =0,4.Вероятность того, что будет ровно одно попадание находим по формуле

.

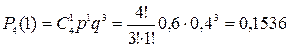Наивероятнейшее число попаданий

,

.

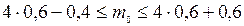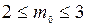Таким образом, имеется два наивероятнейших числа 2 или 3.

Пример 2. Вероятность наступления события А в каждом из одинаковых и независимых испытаний равна 0,7. Найти вероятность того, что в 1600 испытаниях событие А наступит: а) ровно 1100 раз; б) от 1100 до 1200 раз.

Решение. Р(А) = p = 0,7 - вероятность появления события А при одном испытании. Р(А) = q =1 – 0,7 = 0,3 – вероятность непоявления события А при одном испытании.

а) Воспользуемся локальной формулой Муавра-Лапласа

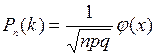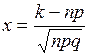, где и .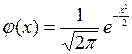

По условию n= 1600, k= 1100.

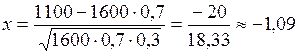
По таблице ([5], приложение 1) j(-1,9)=j(1,9)=0,223.

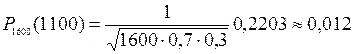
б) Воспользуемся интегральной формулой Лапласа

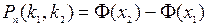, где ;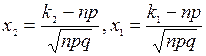

.

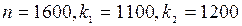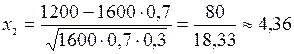
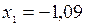
По таблице ([5], приложение 2) Ф(4,36) » 0,5, Ф(-1,09)= - 0,3621.

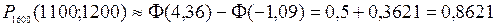
Теоретические вопросы к разделу 3.

1. Формула Бернулли.

2. Локальная формула Муавра-Лапласа.

3. Интегральная формула Муавра-Лапласа.

4. Формула Пуассона.

Задание к разделу 3.

Куплено n лотерейных билетов. Вероятность выигрыша на один лотерейный билет р=0,3. Найти а) вероятность того, что из n билетов k билетов выиграют; б) наивероятнейшее число выигрышных билетов.

№
n
k