Свойства условного математического ожидания

Многие свойства условного математического ожидания аналогичны и, в основном, доказываются аналогично соответствующим свойствам математического ожидания. В дальнейшем в этом пункте равенства и неравенства понимаются в смысле почти наверное и, при необходимости, предполагается существование у случайных величин математических ожиданий и вторых моментов.

1. 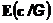=с

2.

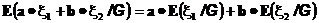
3. Если 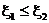, то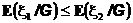

4.

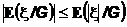
5.

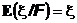
6.

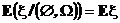
7. Если 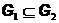, то

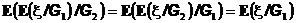
8.

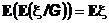
9. Пусть 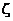- G – измерима, тогда

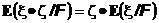
10. Пусть 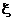не зависит от сигма-алгебры G, (т.е. любые события 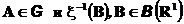независимы) , тогда

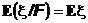
11. 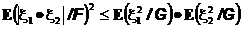-неравенство Коши -Буняковского

12. Если функция 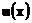выпукла как 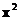, то 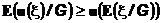-неравенство Йенсена

13.

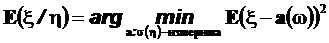
14. Для условных математических ожиданий верны теоремы о предельном переходе под знаком интеграла Лебега, в частности теорема о монотонной сходимости.

·

Попробуйте доказать эти свойства. Самостоятельное доказательство поможет лучше понять определение условного математического ожидания

· Доказательства свойств 1)- 8) непосредственно следуют из определения условного математического ожидания, неравенства 11), 12) доказываются также как аналогичные неравенства для математического ожидания, свойства 9) и 10) сначала устанавливаются для простых функций, а затем переносятся на общий случай с помощью теорем о предельном переходе под знаком интеграла Лебега. Доказательство свойства 13) с учетом 6) и 9) аналогично доказательству соответствующего экстремального свойства математического ожидания. 14) получается применением теоремы для монотонной сходимости для интеграла Лебега.

Определение условной вероятности, условного распределения и условной плотности

Условная вероятность

Условной вероятностью события Aотносительно сигма-алгебры G называется случайная величина

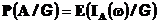
Аналогично определяется условная вероятность относительно случайной величины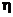

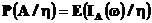
Заметим, что условная вероятность это функция двух переменных: 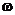(как случайная величина) и A.Нетрудно видеть, что условная вероятность для каждого 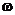является почти наверное неотрицательной конечно-аддитивной по A функцией такой , что

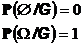
В силу неоднозначности определения условного математического ожидания (с точностью до значений на множествах нулевой вероятности) вообще говоря нельзя утверждать, что условная вероятность для любого фиксированного 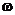( и даже для почти всех 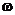) является вероятностью. Однако если, например, ограничиться только распределениями на борелевских сигма-алгебрах, то доказать существование счетно-аддитивного варианта условной вероятности оказывается возможным.

Условное распределение

Пусть 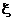и 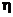- случайные векторы произвольной конечной размерности (например, k и s ) заданные на некотороми вероятностном пространстве

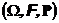
Функция 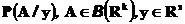называется условным распределением случайной величины 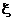при условии 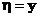, если

1. При каждом 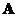условная вероятность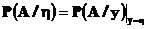

2. При каждом 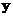функция 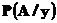является распределением

Замечательным является тот факт, что для любых случайных векторов условное распределение существует. Доказательство этого утверждения и более общие условия существования условного распределения можно найти, например, в книге Ширяева. Для условного распределения часто используют следующее обозначение:

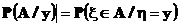
Если условное распределение при каждом 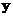имеет плотность относительно некоторой меры 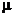, то эта плотность называется условной плотностью распределения случайной величины 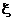при условии 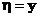и обозначается

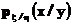
Обозначив 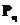распределение случайной величины 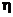, используя свойства 8) и 9) условного математического ожидания получим, что для любых борелевских подмножеств

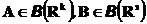
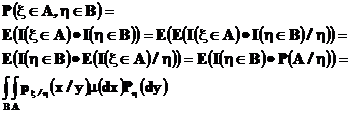
Наоборот, если функция 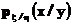удовлетворяет соотношению

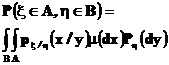
то она, очевидно, является условной плотностью.

Если распределение 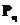имеет плотность 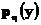относительно меры 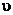, то

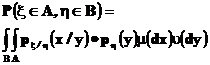
Данное соотношение означает, что функция

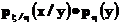
является совместной плотностью вектора 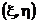относительно произведения мер