Теорема непрерывности для характеристических функций.

Для того, чтобы

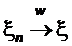
необходимо и достаточно, чтобы для всех t

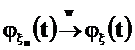
Доказательство.

Пусть

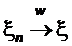
Тогда используя ограниченность, непрерывность по x для любого t функции 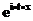и теорему Хелли-Брея получаем

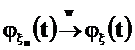
Доказательство необходимости завершено.

Пусть теперь

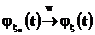
Тогда, используя теорему о выборе, мы можем извлечь из любой подпоследовательности последовательности функций распределения 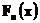случайных величин 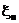, сходящуюся к некоторой функции 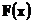подпоследовательность 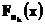, при этом соответствующая подпоследовательность характеристических функций 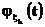как подпоследовательность сходящейся последовательности характеристических функций сходится к 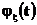. Покажем, что функция 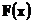является функцией распределения.

Полагая

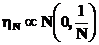
и применяя к паре функций 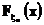, 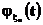равенство Парсеваля

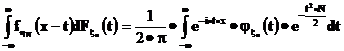
получаем, что, с одной стороны, для любого x

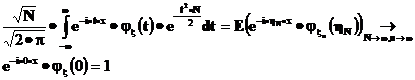
С другой стороны, для любых N, n и х

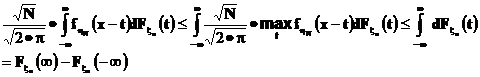
Таким образом:

1.Функция 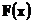является собственной функцией распределения

2.Из любой подпоследовательности последовательности функций распределения 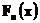случайных величин 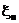можно извлечь сходящуюся к 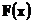подпоследовательность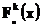

3.Характеристическая функция 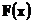совпадает с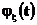

·

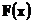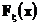Используя теорему единственности для характеристических функций получаем из 1) и 3), что функции и совпадают и из 2) следует утверждение второй части теоремы (доказательство от противного).

Доказательство завершено.

Предельные теоремы теории вероятностей

Предельные теоремы представляют собой утверждения, устанавливающие условия сходимости (в том или ином смысле) последовательности случайных величин или последовательности распределений для некоторого класса вероятностных моделей. Существеннная роль, которую играют в теории вероятностей предельные теоремы объясняется тем, что в ряде случаев они представляют единственный способ качественного и количественного анализа сложных вероятностных моделей. Эти теоремы устанавливают близость (в некотором строго определенном смысле) одних вероятностных моделей другим. Применение предельных теорем позволяет выделить главные и второстепенные с количественной точки зрения свойства исследуемой вероятностной меры. Первой вероятностной моделью, для которой были получены предельные теоремы, является схема суммирования независимых слагаемых.

Схема суммирования независимых слагаемых

Классическая схема

Рассмотрим последовательность независимых одинаково распределенных случайных величин

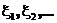
Обозначим

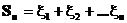
В данной схеме обычно исследуется предельное поведение величины

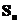и ее нормированных вариантов 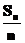и 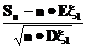при больших n.

Схема серий

Рассмотрим последовательность векторов возрастающей размерности (иначе – серий), состоящих из независимых случайных величин

…

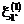
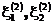
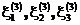
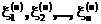
Обозначим

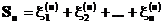
Распределение случайных величин внутри и между сериями не предполагается одинаковым и может зависеть от n.

В данной схеме также исследуется предельное поведение величины

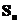и ее нормированных вариантов 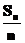и 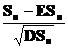при больших n. Схема серий является обобщением классической схемы суммирования. Примерами предельных теорем для частного случая классической схемы (схемы Бернулли) могут служить теорема Пуассона и закон больших чисел в форме Бернулли.

Современные предельные теоремы являются обычно собирательными утверждениями, т.е. такими утверждениями, которые справедливы сразу для большого класса объектов (в нашем случае вероятностных моделей). Первым примером предельной теоремы такого рода является закон больших чисел в форме Чебышева.