Сходимость и свойства почти наверное

В теории вероятностей используется несколько понятий сходимости случайных величин. Одна из них – поточечная сходимость (сходимость в каждой точке 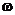) использовалась при определении интеграла Лебега. Следующий вид сходимости называется сходимость почти наверное (п.н.)

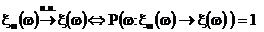
Последовательность сходится почти во всех точках (кроме тех, вероятность которых равна 0).

Более общо, говорят что некоторое свойство, относящееся к одной или нескольким случайным величинам выполнено почти наверное, если оно выполнено для всех точек 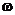, кроме множества точек имеющего вероятность 0.

Докажите!

Например,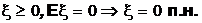

Если

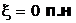
то

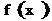
Теорема Лебега о мажорируемой сходимости

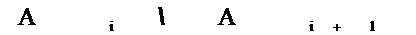
Неравенства

Неравенство Маркова

Доказательствоследует из очевидного неравенства

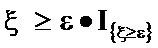
и свойств 1) и 3) математического ожидания.

Неравенство Чебышева. Дисперсия

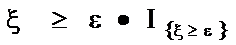
Доказательствоследует из неравенства Маркова, примененного к случайной величине

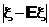
Величина

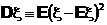
называется дисперсия случайной величины. Она является естественной мерой разброса случайной величины относительно ее математического ожидания. Очевидны следующие свойства дисперсии.

1.

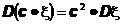
2.

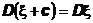
3. 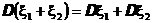для независимых с.в.

Следующее свойство выявляет смысл математического ожидания и дисперсии, как экстремальных характеристик с.в. Будем обозначать точку экстремума (минимума и максимума) функции так

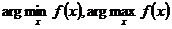
Тогда

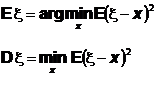
Для доказательства заметим, что по переменной xвыражение

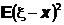
представляет собой квадратный трехчлен.

Неравенство Коши-Буняковского-Шварца. Ковариация

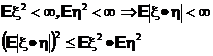
Доказательство.Если

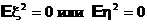
то

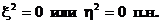
и неравенство превращается в равенство.

Если

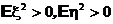
то, используя очевидное неравенство

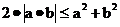
получаем

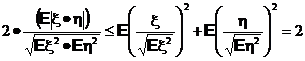
что эквивалентно доказываемому неравенству.

Применяя неравенство КБШ к случайным величинам

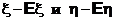
получаем

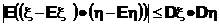
Величина

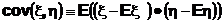
называется ковариация случайных величин

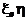
и, как мы увидим в дальнейшем, является естественной мерой связи этих случайных величин между собой.

Величина

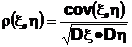
называется коэффициент корреляции случайных величин

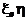
Из неравенства КБШ следует, что

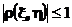
и если

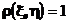
то между этими случайными величинами существует (почти наверное) линейная зависимость

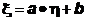
с положительным коэффициентом a. В этом случае говорят, что случайные величины положительно коррелированы. Если

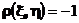
то коэффициент a отрицателен и случайные величины отрицательно коррелированы. Коэффициент корреляции используют как меру зависимости случайных величин.

Неравенство Йенсена.Выпуклые функции

Функция f(x) называется выпуклой (как 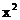), если

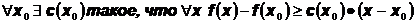
Например, функции 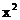, exp(x) выпуклы.

Для выпуклых функций справедливо неравенство Йенсена

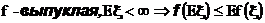
Доказательствоследует из определения выпуклой функции, если в нем положить

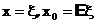
и воспользоваться свойствами 1) 2) 3) математического ожидания.