Точки непрерывности и разрыва функции распределения

Множество на прямой называется всюду плотным, если в любой окрестности любой точки прямой найдется точка из этого множества

Заметим, что, в силу своей монотонности, любая функция распределения имеет не более чем счетное число точек разрыва. Поэтому между любыми двумя точками на прямой содержится бесконечно много (континуум) точек непрерывности функции распределения. Ясно также, что для определения функции распределения во всех точках достаточно знать ее только в точках непрерывности или более общо на любом всюду плотном множестве.

Несобственные функции распределения

Условие 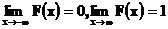отражает условие нормировки . Многие утверждения относительно функции распределения легко переносятся на так называемые несобственные функции распределения, т.е. функции удовлетворяющие условиям 1),2),4) и условию

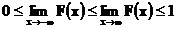. В дальнейшем мы будем иногда пользоваться этим понятием. Несобственным функциям распределения соответствуют по теореме Каратеодори меры на прямой с условием

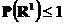
Дискретные распределения на прямой

Основные дискретные распределения - равномерное, биномиальное, геометрическое, пуассоновское, можно рассматривать как распределения на пространстве

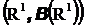
так как множество целых чисел содержится в множестве действительных чисел и борелевская сигма-алгебра содержит все одноточечные множества. Добавим к ним еще одно важное распределение – вырожденное, и построим графики функций распределения для этих распределений.

Вырожденное распределение

Вырожденное распределение это такая вероятностная мера, которая приписывает вероятность 1 одному элементарному исходу, т.е.

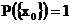
а всем остальным исходам, естественно, ничего не достается

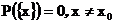
Говорят, что распределение вырождено в точке x₀.

Построим функцию распределения вырожденного распределения.

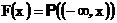
поэтому

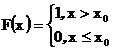
На следующем рисунке приведен график функции распределения вырожденого в нуле распределения.

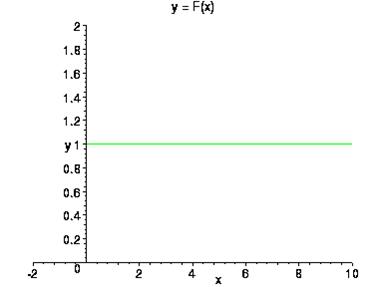
Случайная величина, имеющая вырожденное распределение называется вырожденная случайная величина.

Бернуллиевское распределение

Бернуллиевское распределение приписывает вероятность p точке 1 и 1-pточке0 , т.е.

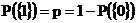
Построим функцию распределения вырожденного распределения

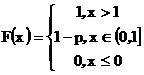
На следующем рисунке приведен график функции распределения бернуллиевского распределения при p = 0,7

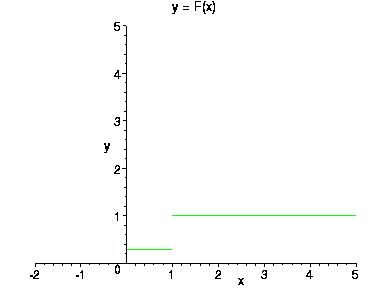
Видно, что функция распределения бернуллиевского распределения равна сумме двух вырожденных функций распределения – в 0 и 1 с множителями 0,3 и 0,7.

Случайная величина, имеющая бернуллиевское распределение называется бернуллиевская случайная величина.

Биномиальное распределение

Биномиальное распределение приписывает точке k вероятность

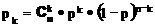
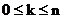
Построим функцию распределения биномиального распределения

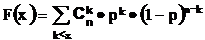
На следующем рисунке приведен график функции распределения биномиального распределения при n=5, p=0,7.

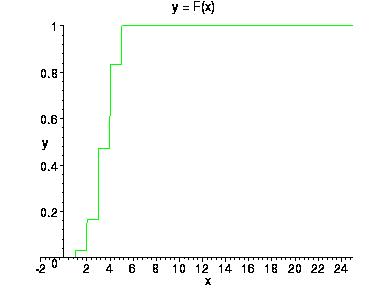
На следующем рисунке приведен график функции распределения биномиального распределения при n=20, p=0,5.

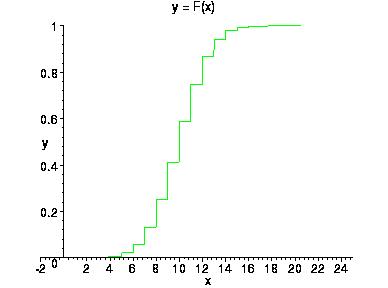
Случайная величина, имеющая биномиальное распределение называется биномиальная случайная величина. Для биномиального распределения используют обозначение

.

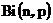В частности, бернуллиевское распределение это

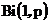
вырожденное в нуле распределение это

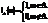
Обозначение

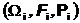
означает, что случайная величина

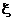
биномиальная с параметрами n и p.