Распределения случайных величин и векторов

В данной главе рассматриваются математические модели в которых пространство элементарных исходов представляет собой действительную прямую или пространство векторов с действительными координатами. В главе содержатся способы построения вероятностных мер (распределений) на борелевских алгебрах, приводятся наиболее важные распределения и примеры практических ситуаций, в которых они возникают. Вначале нам потребуются некоторые факты из теории меры.

Построение меры на прямой

Сигма-конечная мера

Мера называется сигма-конечной, если существует полная группа событий такая, что мера каждого из событий конечна. Ясно, что вероятность является сигма-конечной мерой.

Теорема Каратеодори

Следуюшая теорема общей теории меры дает способ построения меры на измеримом пространстве. Она приводится без доказательства.

Теорема Каратеодори.

Пусть

пространство элементарных исходов, A – алгебра,

.

Пусть

сигма-конечная мера, заданная на

Тогда существует и единственна сигма-конечная мера

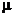
заданная на

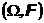
такая что

Продолжение и сужение меры

Мера

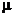
называется продолжение меры

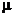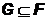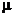Если мера задана на сигма –алгебре и - другая сигма-алгебра, то меру совпадающую с на 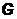называют сужением меры 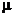на сигма-алгебру

Часто для меры, ее продолжения и сужения используют одинаковые обозначения.

Теперь можно переходить к построению вероятностных мер на прямой.

Функция распределения

Функция действительного аргумента

назвается функция распределения, если она удовлетворяет следующим условиям

Важность функции распределения состоит в том, что каждой такой функции соответствует единственная вероятность P на борелевской сигма-алгебре прямой, для которой

и, наоборот, каждой вероятности на борелевской сигма-алгебре прямой соответствует некоторая функция распределения

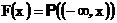
Действительно, если P –вероятность, то функция, определенная по формуле

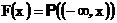
будет, очевидно, удовлетворять свойствам 1) и 2).

Свойства 3),4) следуют из свойства непрерывности вероятностной меры:

если

то

если

то

если

то

Для того, чтобы доказать обратное, заметим, что алгебра, состоящая из конечных объединений отрезков вида

порождает борелевскую сигма-алгебру. Функция

конечно аддитивна. Для того, чтобы воспользоваться теоремой Каратеодори, необходимо доказать ее счетную аддитивность (или непрерывность). А вот этого мы делать не будем, так как это обычно доказывается ( или не доказывается в курсе функционального анализа). Тех, кто очень хочет прочитать доказательство счетной аддитивности этой функции, отправляем к книгам Боровкова и Ширяева (Дополнительная литература).

Если нам будет важно отметить, какая вероятность соответствует функции распределения F, будем отмечать это так