Равновесие пространственной системы параллельных сил

Для пространственной системы параллельных сил можно со­ставить три уравнения равновесия.Если силы параллельны оси Z, то имеем следующие уравнения равновесия:

1. .

2. .

3. .

Задача 2.Квадратная однород­ная плита весом Р нахо­дится в равновесии. Определить реакции связей, если Р = 100 Н; F = 20 H (рис. 4.6).

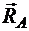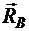Решение. Рассмотрим равновесие плиты под действием системы па­раллельных сил , и реакций связей , , . Составим три уравнения равно­весия:

1.

2.

3.

Рис. 4.6

Находим из (2)

,

из (3)

,

из (1)

.

Ответ. .

Минус показывает, что реакция связей направлена про­тивоположно направлению, показанному на рис. 4.6.

Задача 3.При повреждении одной из двух петель прямоугольной парниковой рамы ABDE ее удерживают в горизонтальном положении двумя вертикальными стержнями FJ и KL. Вес рамы G= 80 Н. Расстояния: BF=1/4 BD; ND=1/5 BD; KN =1/2 ED. Определить реакцию шарового шарнира (петли) А и усилия в стержнях FJ и KL (pиc. 5.2.1).

Решение. Рассматриваем равновесие сил, приложенных к раме. Прикладываем к раме в центре тяжести С задаваемую силу - вес рамы (рис. 5.2.1). Отбрасывая связи, прикладываем к раме их реакции. Реакции сжатых стержней и , равные усилиям в стержнях, направляем вертикально вверх. Реакция шарового шарнира 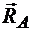может иметь любое направление, но при условии, что остальные силы , и , приложенные к раме, вертикальны, реакция 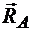тоже имеет вертикальное направление.

Рис. 5.2.1 Рис. 5.2.2

Для полученной системы вертикальных сил, из которых три силынеизвестны, составляем три уравнения равновесия параллельных сил в пространстве. Начало координат помешаем в одну из опорных точек (A),осьz направляем параллельно силам,осихи у проводим по краям рамы.

Уравнения равновесия параллельных сил имеют следующий вид:

(1)

(2)

(3)

В уравнение (2) подставляем BN=4/5 BD, BF=1/4 BD и, сокращая, получаем

; (1а)

; (2а)

. (3а)

Подставляем значение G=180 H, решая систему двух первых уравнений и находим R_K и R_F:

,

или

.

Вычитая из одного уравнения другое, находим:

.

Из уравнения (3) определяем R_A:

.

Задача 4.Дано: Р=5 кН, М=6 кНм, l=0,8 м, F₃=8 кН, F₁=4 кН. Найти: реакции связей А, В и стержня (рис. 5.2.2).

Рис. 5.2.2

Решение. Рассмотрим равновесие плиты. На нее действуют сила тяжести , силы , пара сил с моментом и реакции связей А( ), В( ) и стержня (считаем его растянутым).

Составляем уравнения равновесия пространственной системы сил:

, ;

,

;

,

;

, ;

,

.

XA	YA	ZA	YB	ZB	N
кН
2,33	–6,7	–1	–4,8

Задача 5.. Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 5.2.4). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0,1N.

Рис. 5.2.4

На шкив 2 действуют силы натяжения ремней Т_г = 30 Н, Т₂ = 57 Н. Груз Q = 18 Н висит на нити, навитой на шкив 3. Определить силу давления N и реакции шарниров в условии равновесия вала. Учесть веса шкивов: Р_г = 35 Н, Р₂ = 10 Н, Р₃ = 15 Н. Все нагрузки действуют в вертикальных плоскостях. Известны радиусы шкивов, R₁= 26 см, R₂ = 10 см, R₃ = 11 см и расстояния между характер­ными точками вала: а = 22 см, b = 25 см, с = 26 см, d = 26 см. Общая длина вала L = a + b + c + d; α =30°.

Рис. 5.2.5

Решение

1. Действие цилиндрических опор А и В заменим реакциями Z_A, Х_А и Z_B, Х_В (рис. 5.2.5). Вес вала G приложим в центре. Вес груза изобразим вектором Q.

2. Для определения силы давления составляем уравнение моментов
относительно оси вала:

.

Уравнение содержит одну неизвестную F. Линии действия остальных сил пересекают ось у и их моменты относительно оси вала равны нулю.

Из полученного уравнения находим

По условию N = F/0,1 = 27,692 Н.

3. Определяем вертикальные реакции шарнирных опор вала. Для
этого составляем два уравнения моментов относительно горизонтальных осей, проходящих через шарниры А и В. Рассматриваем для удобства проекцию всех сил на плоскость zy (рис. 5.2.6). Таким образом вычисление моментов относительно осей сводим к плоской задаче вычисления моментов относительно точек А и В.

Знаки моментов сил определяем как в задачах плоской статики: момент силы, вращающей тело вокруг моментной точки против часовой стрелки считается положительным, по часовой стрелке — отрицательным. Моменты сил, перпендикулярных плоскости zy (и поэтому не изображенных на рис. 5.2.9), относительно любой ее точки равны нулю.

Рис. 5.2.6

Решая уравнения

находим Z_A = –11,324 H, Z_B = 75,574 H.

4. Проверяем правильность нахождения вертикальных реакций,
составляя уравнение равновесия в проекции на ось z (рис. 5.2.6):

5. Определяем горизонтальные реакции опор вала. Для этого со­ставляем два уравнения моментов относительно осей, совпадающих с
линиями действия вертикальных реакций шарниров. Рассматриваем
горизонтальную проекцию силовой схемы (рис. 5.2.7):

Решая уравнения, находим Х_А = 25,100 Н, Х_В = –124,792 Н.

6. Проверяем правильность нахождения горизонтальных реакций,
составляя уравнение равновесия в проекции на ось х вдоль линии действия горизонтальных реакций:

Рис. 5.2.7

Результаты расчетов в Н заносим в таблицу:

N	XA	ZA	XB	ZB
27,692	25,100	-11,324	-124,792	75,574

Задача 6. Груз весом Р поднимается с помощью лебедки (рис. 5.2.8). К концу рукоятки лебедки приложена вертикальная сила Q. Длина рукоятки l. Расстояние КМ = а, СЕ =d, радиус малойшестерни равен r, радиус большой — R, радиус барабана — R₁, АВ=L₁. Рукоятка лебедки расположена горизонтально. Плоскость, перпендикулярная осям валов и проходящая через подшипники А и С, отстоит от плоскости зубчатых колес на расстоянии l₁. CD = 2l₁. Угол зацепления (угол между усилием в зубчатом зацеплении и нормалью к колесам в точке касания) принять равным 33° (рис. 5.2.9, 5.2.10).

Рис. 5.2.8

Определить величину силы Q и реакции всех подшипников.

Решение. Рассмотрим равновесие вала CD (рис. 5.2.9) и вала АВ (рис. 5.2.10).

Рис. 5.2.9 Рис. 5.2.10

Уравнения равновесия вала CD:

Уравнения равновесия вала АВ:

Используя полученные уравнения равновесия, определяем неизвестные.

Задача 7. Коленчатый вал может вращаться в цилиндрических под­шипниках А и В. На конце вала насажана шестерня радиусом R. В центре D шейки приложена сила Q, лежащая в плоскости перпендикулярной оси вала и направленная параллельно оси z. Определить модуль силы F, возникающей в зубчатом зацеплении, и реакции коренных подшипников в точках А и В. На рис. 5.2.11: Ау — ось вала, ось Ах перпендикулярна оси вала и параллельна общему перпендикуляру, соединяющему ось вала с осью шатунной шейки.

Рис. 5.2.11

Ось Az перпендикулярна плоскости Аху. Сила F лежит в плос­кости шестерни под углом α к оси z. Длина кривошипа (расстояние между осью шатунной шейки и осью вала) равна r.

Решение. Рассмотрим равновесие коленчатого вала. Применив принцип освобождаемости от связей, отбросим цилиндрические шарниры А и В и заменим их действие реакциями связей. Цилиндрические шарниры не препятствуют перемещению тела по оси у, поэтому их реакции можно представить двумя составляющими в точке A(Y_A, Z_A) и в точке B(Y_B, Z_B).

Таким образом, система сил, действующих на коленчатый вал (Y_A, Z_A, Y_B, Z_B, F, Q), эквивалентна нулю. В этой системе пять неизвестных, то есть задача статически определена.

Составим уравнения равновесия.

Используя полученную систему уравнений, составляем алгоритм для определения реакций связей: