Контрольные задачи к главе 4 «Функции случайных величин»

4.1. Из накопителя перед первой технологической операцией детали забираются на обработку регулярно через каждые 10 минут. Из накопителя перед второй технологической операцией детали забираются на обработку регулярно через каждые 30 минут. Найти в процентах коэффициент вариации суммарного времени ожидания детали в накопителях (при случайном ее попадании туда).

4.2. Известно, что 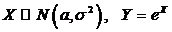. Найти закон распределения Y.

4.3. На окружности радиуса 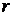случайным образом располагаются две точки, которые затем соединяются между собой и с центром окружности. Найти математическое ожидание площади полученного треугольника.

4.4. Пусть X, Y, Z – случайные величины: X – выручка фирмы, Y – ее затраты, Z = X – Y – прибыль.

X:		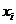				Y: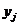
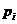		1/3	1/3	1/3		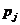		1/2	1/2

Найти распределения прибыли Z .

4.5. Вес гайки и болта являются нормально распределенными величинами с математическими ожиданиями 15 и 40 гр.и средними квадратическими отклонениями 2 и 5 гр., соответственно. Ковариационный момент этих величин равен 7 гр.². Найти среднее квадратическое отклонение веса всего узла «гайка + болт».

4.6. Дискретные независимые СВ заданы своими распределениями:

X			Y
P	0.3	0.7	P	0.6	0.4

Найти коэффициент вариации величины Z = X + Y.

4.7. Независимые СВ X и Y заданы плотностью распределения:

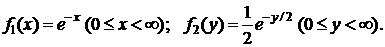
Найти плотность распределения СВ Z = X + Y.

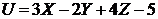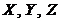4.8. Ошибка прибора выражается функцией , где – так называемые первичные ошибки, представляющие собой систему случайных величин, которая характеризуется математическими ожиданиями 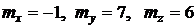и корреляционной матрицей 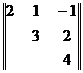. Найти среднее квадратическое отклонение ошибки прибора.

4.9. Дискретная случайная величина 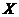имеет ряд распределения, представленный в таблице.

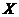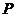	0,1	0,4	0,3	0,2

Найдите математическое ожидание и дисперсию величины .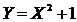

4.10. Связь между нормально распределенными показателями Х и Y выражается зависимостью Y = 1,3х + 0,5. При этом дисперсия Y в 4 раза выше дисперсии Х. Найти степень тесноты связи величин Х и Y.

4.11. Показатель Y выражается формулой 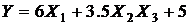, где 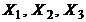представляют собой величины с математическими ожиданиями 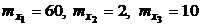и средними квадратическими отклонениями 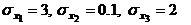Нормированная корреляционная матрица системы имеет вид: 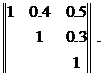Найти среднее квадратическое отклонение СВ Y.

4.12. Случайные величины 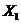и 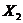имеют математические ожидания 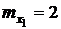, , 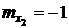дисперсия 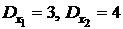и ковариацию 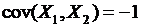. Найдите математическое ожидание и дисперсию случайной величины

.

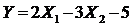4.13. Независимые случайные величины 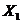и 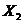имеют экспоненциальное распределение с параметрам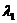и и 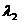соответственно. Найти математическое ожидание случайной величины .

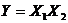4.14. Два стрелка независимо один от другого производят по одному выстрелу в мишень. Вероятность попадания для каждого из стрелков равна 0,6. Пусть случайные величины X и Y означают число попаданий в мишень для первого и для второго стрелка соответственно. Построить закон распределения и найти математическое ожидание для случайной величины: .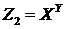

4.15. СВ X задана плотностью распределения f(x) = (1/2)sin(x) в интервале (0,p); вне интервала f(x) = 0. Найти дисперсию величины Y=X².

4.16. Случайная величина X задана плотностью вероятности 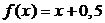в интервале (0;1); вне этого интервала 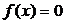. Найти математическое ожидание функции .

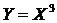4.17. Две случайные величины (X и Y) имеют характеристики: 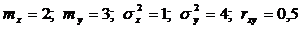. Определить дисперсию суммы и разности этих величин.

4.18. Две независимые случайные величины (X и Y) распределены равномерно: Х на интервале[- 5; 1], Y на интервале [3; 6]. Найти математическое ожидание и дисперсию случайной величины 7Х - 9Y + 8.

4.19. Ребро куба измерено приближенно, причем 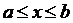. Рассматривая ребро куба как случайную величину X, распределенную равномерно в интервале (a, b), найти математическое ожидание объема куба.

4.20. Дискретные независимые СВ заданы своими распределениями:

X			Y
P	0.3	0.7	P	0.6	0.4

Найти коэффициент вариации величины Z = 2X + 3Y.

4.21. Предприятие состоит из двух подразделений. Месячная прибыль каждого подразделения является нормально распределенной величиной с математическими ожиданиями 550 и 400 тыс. руб. и средними квадратическими отклонениями 60 и 50 тыс. руб., соответственно. Ковариационный момент этих величин равен 70 тыс. руб.² Найти коэффициент вариации прибыли всего предприятия.

4.22. Один станок дает в среднем 3% брака, другой – 5%. Производительности станков одинаковы. Каков коэффициент вариации числа бракованных изделий в общей продукции из 100 деталей?

4.23. Две СВ (X и Y) имеют характеристики:

.

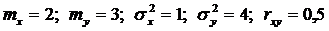Определить дисперсию суммы этих величин.

4.24. Вес гайки и болта являются нормально распределенными величинами с математическими ожиданиями 10 и 40 гр. и средними квадратическими отклонениями 2 и 5 гр., соответственно. Ковариационный момент этих величин равен 7 гр.². Найти среднее квадратическое отклонение веса всего узла «гайка + болт».

4.25. Погрешность в изготовлении детали образуются в результате суммарного воздействия трех факторов А, В и С. Их характеристики известны:

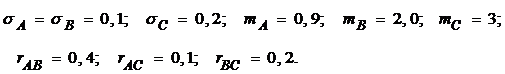
Найти среднее квадратичное отклонение погрешности изготовления детали.

4.26. Даны законы распределения двух независимых случайных величин Х и Y

Х	–1
Р	0,2	0,3	0,1	0,4

Найти характеристики М(ХY – 5Х + 2Y – 7), D(8Х – 3Y + 4).

4.27. Независимые СВ X и Y заданы плотностью распределения:

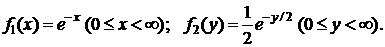
Найти плотность распределения СВ Z = X + Y.

Задачи, предлагаемые для решения на практических занятиях по первому разделу курса «Теория вероятностей»