Найти функцию распределения F(x).

2.8. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

2.9. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения числа стандартных деталей среди отобранных.

2.10. Случайная величина 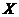имеет плотность распределения

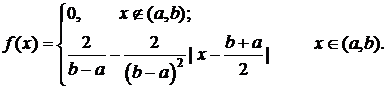
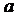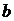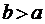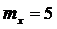причем и не известны, но , а и 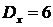. Найдите 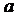и .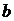

2.11. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Вычислить математическое ожидание и дисперсию числа таких договоров среди наудачу выбранных четырех.

2.12. Из пяти роз две белые. Составить закон распределения случайной величины, выражающей число белых роз среди двух одновременно взятых.

2.13. Среди 15 собранных агрегатов 6 нуждаются в дополнительной смазке. Составить закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наудачу выбранных из общего числа.

2.14. Из поступивших в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Найти математическое ожидание и дисперсию числа просмотренных часов.

2.15. Абонент забыл последнюю цифру нужного ему номера телефона, однако помнит, что она нечетная. Найти математическое ожидание и дисперсию числа сделанных им наборов номера телефона до попадания на нужный номер, если последнюю цифру он набирает наудачу, а набранную цифру в дальнейшем не набирает.

2.16. Вероятность отказа за время испытаний на надежность для каждого прибора серии равна p. Определить математическое ожидание числа приборов, давших отказ, если испытанию подверглись N приборов.

2.17. Дискретная случайная величина X принимает 3 возможных значения: 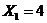с вероятностью 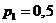; 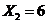с вероятностью 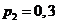и 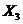с вероятностью 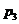. Найт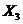и и 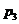, зная, что M(X) = 8.

2.18. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится 5 изделий. Найти математическое ожидание случайной величины X – числа партий, в каждой из которых содержится ровно 4 стандартных изделия, если проверке подлежат 50 партий.

2.19. Найти дисперсию случайной величины X – числа появлений события A в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что M(X) = 0,9.

2.20. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15; 25).

2.21. Дана функция: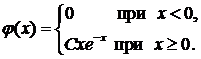

При каком значении параметра C эта функция является плотностью распределения некоторой непрерывной случайной величины X? Найти математическое ожиданий и дисперсию случайной величины X.

2.22. Величина X задана плотностью вероятности 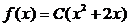в интервале (0;1), вне этого интервала 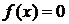. Найти: постоянный параметр С; математическое ожидание величины X.

2.23. Случайная величина X в интервале (0;1) задана плотностью вероятности 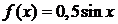; вне этого интервала 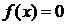. Найти дисперсию X.

2.24. Устройство состоит из N элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна p. Необходимо найти математическое ожидание и дисперсию этой случайной величины.

2.25. Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0.25. Определить среднее квадратическое отклонение числа попаданий при трех выстрелах.

2.26. Среднее число клиентов, посещающих страховую компанию за 10 мин., равно трем. Найти вероятность того, что в ближайшие 5 минут придет хотя бы один клиент.

2.27. Среднее время настройки прибора составляет 5 минут и подчинено показательному распределению. Мастер уже потратил 5 минут на настройку очередного прибора. Найти вероятность того, что он затратит еще не менее трех минут на настройку этого прибора.

2.28. В отдел заказов в среднем приходит 18 клиентов в час. Определить вероятность того, что за две текущие минуты в отдел заказов придет хотя бы один клиент.

2.29. Время ожидания заявки в очереди на процессор подчиняется показательному закону распределения со средним значением 20 секунд. Найти вероятность того, что очередная (произвольная) заявка будет ожидать процессор более 35 секунд.

2.30. Группа студентов в количестве 15 человек проводит собрание в зале, в котором 20 рядов по 10 мест в каждом. Каждый студент занимает место в зале случайным образом. Какова вероятность того, что не более трех человек будут находиться на седьмом месте ряда?

2.31. В партии из 10 деталей имеется 3 нестандартных. Составить закон распределения дискретной случайной величины Х – числа нестандартных деталей среди трех отобранных и найти ее математическое ожидание.

2.32. Непрерывная случайная величина Х распределена по показательному законус плотностью f(x) = 0,7e^-0,7x (x³ 0). Найти вероятность того, что она примет значения из интервала (2; 6).

2.33. Найти математическое ожидание и дисперсию числа выигрышных лотерейных билетов, если их приобрели 20 штук, а вероятность выигрыша по одному билету равна 0,3.

2.34. Найти дисперсию дискретной случайной величины Х – числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,15.

2.35. Для какого из указанных интервалов функция sinx может являться функцией распределения случайной величины Х: (0; ^p/₂), (0; p)? Найти вероятность попадания случайной величины Х в интервал (^p/₆; ^p/₂).

2.36. Функция распределения величины Х имеет вид: F(x) =A+Barctg0,5x; – ¥ < X < +¥. Определить: а) постоянные А и В; б) плотность распределения вероятностей f(х); в) .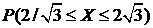

2.37. Длина изготавливаемой станком–автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами а =15 см, s = 0,2 см. Найти вероятность брака, если допустимые размеры детали должны быть 15 ± 0,3 см. Какую точность длины изготовляемой детали можно гарантировать с вероятностью 0,97?

2.38. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание и этой случайной величины.

2.39. Плотность распределения вероятностей случайной величины Х имеет вид f(x) =A 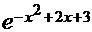. Найти значение параметра А, М(Х), D(X), функцию распределения F(X), вероятность P(- ¹/₃ £ X £ ⁴/₃).

2.40. Найти дисперсию диаметра втулок, представляющего собой случайную величину, распределенную по нормальному закону, если отклонение от математического ожидания, не превосходящее 0,15 см, имеет место с вероятностью 0,8.

2.41. Имеются 4 ключа, из которых только один подходит к замку. Найти математическое ожидание и дисперсию числа попыток открывания замка, если испробованный ключ в последующих попытках не участвует.

2.42. В отдел заказов в среднем приходит 12 клиентов в час. Определить вероятность того, что за три текущие минуты в отдел заказов придет хотя бы один клиент.

2.43.Дискретная случайная величина Х принимает значение х₁ = 1, х₂ = 2, х₃ = 3. Известно также М(Х) = 2,3 и М(Х ²) = 5,9. Найти вероятности, соответствующие возможным значениям величины Х.

2.44.При установившемся технологическом процессе 70 % всей производимой продукции станок–автомат выпускает первым сортом, 30 % – вторым. Составить закон распределения числа изделий первого сорта среди 4 изделий, отобранных случайным образом. Найти математическое ожидание и дисперсию рассматриваемой случайной величины.

Глава 3. Системы случайных величин.

Пример 3.1. Система двух случайных величин подчинена закону распределения с плотностью: 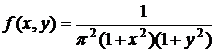. Найти функцию распределения 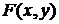. Определить вероятность попадания случайной точки 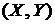в квадрат 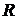с координатами: (1, 1), (0, 1), (1, 0), (0, 0).

Решение.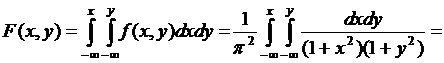

.

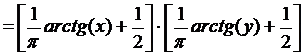Тогда вероятность попадания в прямоугольник :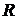

.

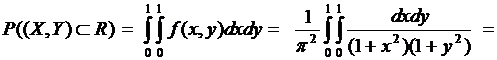
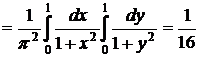Пример 3.2. Плотность распределения системы 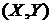имеет вид:

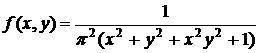. Определить, зависимы или независимы величины 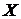и .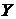

Решение. Разлагая знаменатель на множители, имеем:

.

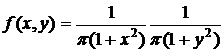Из того, что функция 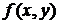распалась на произведение двух функций, из которых одна зависит только от 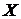, другая - только от 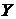, заключаем, что величины 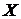и 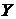должны быть независимы.

Действительно,

.

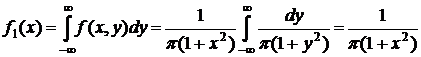Аналогично, .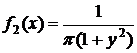

Отсюда убеждаемся, что 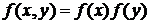, и, следовательно, величины 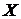и 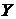независимы.

Пример 3.3. Система случайных величин 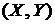подчинена закону распределения с плотностью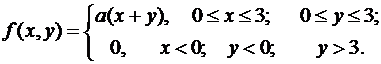

Требуется: определить параметр a; вычислить вероятность попадания точки 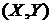в квадрант, ограниченный прямыми 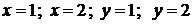; найти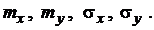

Решение. Найдем параметр a из уравнения .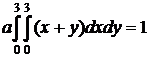

Отсюда: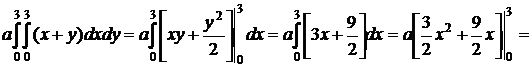

.

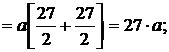
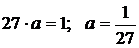Искомая вероятность

.

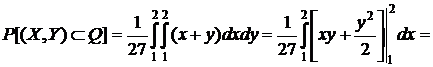
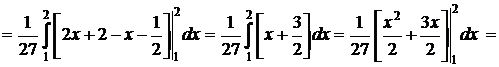
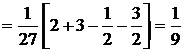По соответствующим формулам вычисляем другие числовые характеристики:

; ;

.

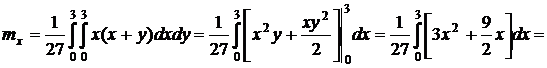
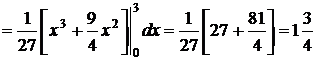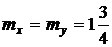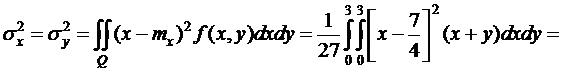
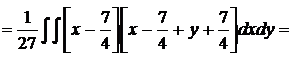
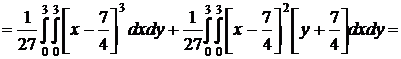
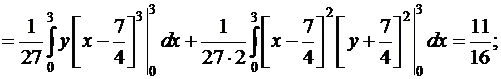
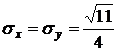Пример 3.4.

События А и В имеют одинаковую вероятность p.

Какова должна быть условная вероятность Р(А|В), чтобы коэффициент корреляции между А и В был равен числу r.

Решение.

Пусть Х = 1 или 0 в зависимости от того, произошло событие А или нет.

Пусть Y = 1 или 0 в зависимости от того, произошло событие B или нет. Обозначим P(A|B) = P(B|A) = p₁.

Тогда P(AB) = pp₁, P( 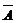B) = p₁(1 - p₁), P(A 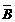) = p(1-p₁), P(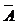 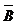) = 1 - 2p + pp₁, т.е. совместное распределение (Х,Y) задается таблицей:

	Y
X
	pp1	p(1 - p1)
	p(1 - p1)	1 - 2p + pp1

Следовательно, M[X] = M[Y] = p, D[X] = D[Y] = p(1-p), M[XY] = pp₁, R_xy = p(p₁ - p), r_xy = 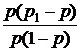= r, т.е. p₁ = P(A|B) = p + r(1 - p).

Пример 3.5.В продукции завода брак вследствие дефекта инструмента составляет 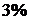, а вследствие дефекта сырья (материала) - 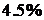. Годная продукция составляет 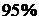. Найти коэффициент корреляции дефектов инструмента и сырья.

Решение. Пусть 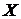- случайная величина, принимающая значение 1, если данное изделие обладает браком вследствие дефекта инструмента, и 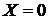- в противном случае.

Аналогично, 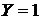, если данное изделие обладает браком вследствие дефекта сырья, и 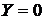, если дефекта сырья не проявился.

По условию .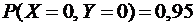

Так как

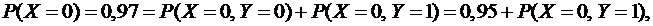то .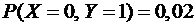

Аналогично находим

.

Совместное распределение величин 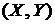задается таблицей:

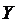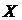	0,025	0,005
	0,020	0,950

Тогда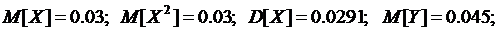

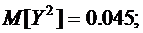
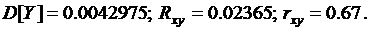
То есть, коэффициент корреляции дефектов инструмента и сырья равен 0,67.