Достаточное условие вогнутости ( выпуклости ) функции.
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если f '' ( x ) > 0 для любого x 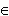 ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x 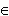 ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.
Билет №29. Асимптоты графика функции
Исследование функции f(x) на минимум и максимум, на точки перегиба облегчают построение графика этой функции. Но кривая y = f(x) может иметь асимптоты, т.е. прямые, к которым неограниченно приближается кривая по мере удаления ее переменной точки в бесконечность.
Поэтому прежде чем построить кривую, нужно провести еще исследование ее уравнения на асимптоты.
Дадим более полное определение асимптоты.
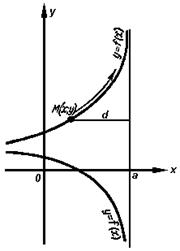 Рисунок 1. Рисунок 1. |
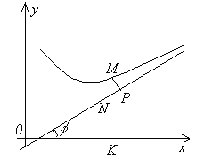
Определение. Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Пусть кривая y = f(x) имеет одну или несколько вертикальных асимптот (рис.1).
Для нахождения вертикальных асимптот кривой y = f(x) нужно отыскать такие значения x = a, при которых y обращается в бесконечность, т.е. при которых 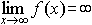 .
.
Уравнение вертикальной асимптоты будет
x = a
В самом деле, из рис.1 непосредственно видно, что расстояние точки M(x; y) от прямой x = a равноd = | x - a |. Когда x ® a, то точка M(x; y) движется по кривой y = f(x), удаляясь в бесконечность, причем ее расстояние d = | x - a | от прямой x = a стремится к нулю и, согласно определению асимптоты, прямаяx = a является асимптотой кривой y = f(x)
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
 Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда,
Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда,
когда 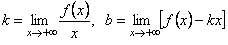 . Аналогичное утверждение верно и при x → –∞.
. Аналогичное утверждение верно и при x → –∞.
Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию 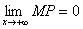 . Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что
. Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что 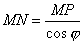 . Так как φ постоянный угол (φ ≠ π/2), то
. Так как φ постоянный угол (φ ≠ π/2), то 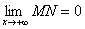 , но
, но
MN = MK – NK = y - yас = f(x) - (kx+b).
Следовательно, мы можем записать следующее равенство 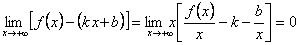 .
.
Так как x → +∞, то должно выполняться равенство 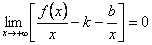 . Но при постоянных k и b
. Но при постоянных k и b 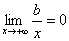 и
и 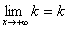 . Следовательно,
. Следовательно, 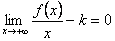 , т.е.
, т.е. 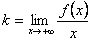 .
.
Если число k уже известно, то 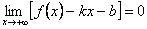 , поэтому
, поэтому 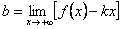 .
.
Для доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство 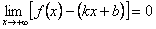 . Действительно
. Действительно

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е. 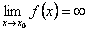 или
или 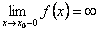 или
или 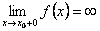 . Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное, если прямая x = x0 является асимптотой, т. о.
. Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное, если прямая x = x0 является асимптотой, т. о. 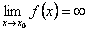 .
.
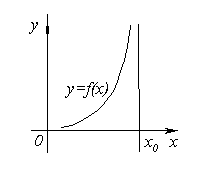 Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Пусть функция 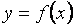 определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции
определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции  . Тогда прямая
. Тогда прямая 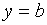 есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 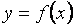 .
.
Может случиться, что 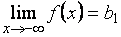 , а
, а 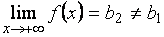 , причем
, причем 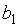 и
и 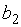 - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов
- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов 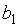 или
или 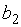 , то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Билет №30. Общая схема исследования функции и построения графика.
1. Д(f)
2. Исследование функции на непрерывность, т.е. точки разрыва вертикальной асимптоты
3. Нахождение наклонных асимптот
4. Четность, нечетность, периодичность
5. Точки пересечения с осью Ох и Оу
6. Точки экстремума, монотонность
7. Точки перегиба, выпуклость, вогнутость
8. График функции
Билет №31. Формула Тэйлора для многочлена. Формула Тэйлора для произвольной функции. Формула Маклорена
