Производная композиции (сложной функции)

Производная обратной функции

Билет №16. Производная неявно заданной функции.

Билет №17. Производная функции, заданной в параметрическом виде.

В зависимости от правила, устанавливающего зависимость между множествами значений величин x и y, различают несколько способов задания функции. Наиболее привычным является представление функции в явном виде . Однако, в некоторых случаях удобно описывать функциональную зависимость множеством пар значений (x; y), которые вычисляются для каждого значения параметра t из промежутка (a; b). К примеру, все пары значений при задают окружность с центром в начале координат радиуса 3.

Определение параметрически заданной функции.

Таким образом, если определены при и существует обратная функция для , то говорят о параметрическом задании функции .

При исследовании параметрически заданной функции иногда приходится находить ее производную по аргументу x. В этой статье мы выведем формулу производной параметрически заданной функции , также остановимся на производной второго и n-ого порядка.

Вывод формулы производной параметрически заданной функции.

Пусть определены и дифференцируемы при , причем и имеет обратную функцию .

Сначала переходим от параметрического задания к явному. При этом получаем сложную функцию , аргументом которой является x.

По правилу нахождения производной сложной функции имеем: . Так как и обратные функции, то по формуле производной обратной функции , поэтому .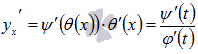

Давайте рассмотрим несколько примеров.

Дальнейшее изложение предполагает умение пользоваться таблицей производных, правилами дифференцирования и формулой производной сложной функции.

Пример.

Найти производную параметрически заданной функции

Решение.

В данном примере , поэтому . Используем выведенную формулу и сразу записываем ответ:

Ответ:

.

ОБРАТИТЕ ВНИМАНИЕ, что производная функции по аргументу x также задается через параметр t, поэтому в ответе нужно указывать и выражение аргумента x через параметр t(строчка переписывается из условия), иначе потеряется связь между значениями производной параметрически заданной функции и аргументом, которому эти значения соответствуют.

Билет №18. Логарифмическая производная.

Логарифмической производной от функции f(x) называется результат логарифмического дифференцирования, т.е. операции, состоящей в последовательном применении к функции f(x) сначала логарифмирования (по основанию е), а затем дифференцирования.

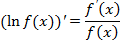
Билет №19. По математическому анализу Дифференциал функции. Инвариантность формулы первого дифференциала.

Дифференциал функции

Функция 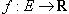называется дифференцируемой в точке 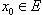, предельной для множества E, если ее приращение Δf(x₀), соответствующее приращению аргумента x, может быть представлено в виде

Δf(x₀) = A(x₀)(x - x₀) + ω(x - x₀), (1)

где ω(x - x₀) = о(x - x₀) при x → x₀.

Отображение 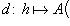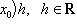, называется дифференциалом функции f в точке x₀, а величина A(x₀)h - значением дифференциала в этой точке.

Для значения дифференциала функции f принято обозначение df или df(x₀), если требуется знать, в какой именно точке он вычислен. Таким образом,

df(x₀) = A(x₀)h.

Разделив в (1) на x - x₀ и устремив x к x₀, получим A(x₀) = f'(x₀). Поэтому 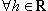имеем

df(x₀) = f'(x₀)h. (2)

Сопоставив (1) и (2), видим, что значение дифференциала df(x₀) (при f'(x₀) ≠ 0) есть главная часть приращения функции f в точке x₀, линейная и однородная в то же время относительно приращения h = x - x₀.

Инвариантность формы первого дифференциала

Если x - независимая переменная, то dx = x - x₀ (фиксированное приращение). В этом случае имеем

df(x₀) = f'(x₀)dx. (3)

Если x = φ(t) - дифференцируемая функция, то dx = φ'(t₀)dt. Следовательно,

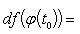
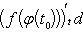
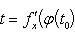
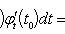
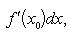
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.

Билет №20. Производные и дифференциалы высших порядков.

Производной n-го порядка f⁽ⁿ⁾(x) называется производная от производной (n-1)-го порядка:

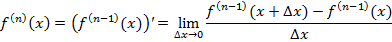
Дифференциалом n-го порядка dⁿy называется дифференциал от дифференциала (n-1)-го порядка как функции x:

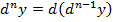
Билет №21. Уравнение касательной и нормали к кривой.

Уравнение касательной к графику функции y = f(x) в точке x₀ равно:

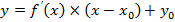
Нормалью к кривой называется прямая, перпендикулярная касательной и проходящая через точку касания:

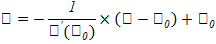
Билет № 22. Теорема Ролля

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

Билет № 23.Теорема Лагранжа
Согласно теореме Лагранжа, если функция f (x) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b), то существует хотя бы одна точка такая, что

Билет №24.Теорема Коши

Пусть функции f (x) и g(x) непрерывны на [a, b] и дифференцируемы на (a, b). Пусть, кроме того, во всех точках интервала (a, b) функция g(x) имеет ненулевую производную g ' (x) ≠ 0. Тогда существует точка c  (a, b), такая, что справедлива формула

Д о к а з а т е л ь с т в о. Покажем сначала, что знаменатель левой части формулы не обращается в ноль. Если допустить, что g(b) = g(a), то по теореме Ролля для функции g(x) найдется точка  (a, b), в которой g ' () = 0. А это противоречит условию, что g ' (x) ≠ 0 на (a, b).
Рассмотрим функцию

.

Функция F(x) на [a, b] удовлетворяет условиям теоремы Ролля: F(x) непрерывна на [a, b], дифференцируема на (a, b), и, кроме того, на концах интервала принимает равные значения F(a) = F(b) = 0. По теореме Ролля для F(x) существует точка c  (a, b) , такая ,что F ' (c) = 0. Так как

,

то

.

Откуда, учитывая, что g '(c) ≠ 0, следует искомое соотношение.

Билет №25. Правило Лопиталя

Билет №26. Необходимое условие экстремума функции одной переменной

Если ф-ия f(x) имеет экстремум в точке x0, то производная её в этой же точке равна нулю или не существует. Доказательство очевидно.

Билет №27. Достаточное условие экстремума функции.

Первый признак.

Дополним, что точки, где производная равна нулю, называются стационарными ; а точки, где производная не существует называются критическими.

Итак, если точка х₀ есть стационарная точка для функции f(x) или если в этой точке не существует для неё двусторонней конечной производной, то точка х₀представляется, так сказать лишь “подозрительной” по экстремуму и подлежит дальнейшему испытанию.

Подставляя в производную f’(x) сначала х<х₀ , а затем х>х₀, устанавливаем знак производной вблизи от точки х₀ слева и справа от неё; если при этом производная f’(x) меняет знак плюс на минус , то налицо максимум, если меняет знак с минуса на плюс, то – минимум ; если же знака не меняет, то экстремума вовсе нет.