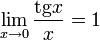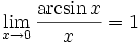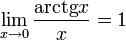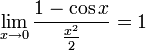Билет №15.Производная сложной и обратной функции.
Ответы на билеты по математическому анализу
Билет №1. Множества и операции над ними
Понятие множества является фундаментальным неопределимым понятием.
Интуитивно под множеством будем понимать собрание определенных вполне различимых объектов, рассматриваемых как единое целое. Отдельные объекты, из
которых состоит множество, называются элементами его. Для обозначения конкретных множеств используются прописные (возможно с индексами) буквы
A, X , A1, X1, для обозначения элементов множества используются строчные (возможно с индексами) буквы x, a, x1,a1. Если x − элемент множества X , то пишут x∈ X (∈− символ принадлежности). Множество, не имеющее ни одного элемента, называют пустым множеством (обозначается Ø). Множество может быть задано перечислением или описанием. Задание множества перечислением заключается в составлении полного списка всех входящих в это множество элементов, заключенных
в фигурные скобки. Например, множества N ={1;2;3;...}, Z ={0;±1;±2;...} − это заданные перечислением множества натуральных и целых чисел соответственно. Задание множества описанием состоит в записи всех свойств его элементов, заключенных в фигурные скобки. Например, множества Q = {х = p/q; p ∈Z; q ∈ N}, I ={x∈ R; x − числа с бесконечной непериодической дробной частью}} –это множества рациональных и иррациональных чисел соответственно, заданные описательно. Множество B называют подмножеством множества A (обозначается B ⊆ A), если любой элемент множества B (∀b :b∈B) является элементом множества A. Если хотят подчеркнуть, что множество A содержит элементы, не принадлежащие B (a∈ A, a∉B), то пишут B ⊂ A (⊂ − символ строгого включения ) .
Например, N ⊂ Z ⊂ Q ⊂ I ⊂ R. Два множества A и B называются равными (обо-
значается A = B ), если одновременно A⊆ B и B ⊆ A. Пересечением или произ-
ведением двух множеств A и B называется множество C (обозначается
C = A I B ), состоящее из всех тех и только тех элементов, которые принадлежат
как множеству A, так и множеству B . Множества A и B называются непересекаю-
щимися, если A I B =Ø. Объединением или суммой двух множеств A и B называ-
ется множество D (обозначается D = A U B ), состоящее из всех тех и только тех
элементов, которые принадлежат или A, или B . Например,
Q U I = R = (−∞;∞) −множество всех действительных чисел. Разностью множеств
A и B называется множество E (обозначается E = A \ B), состоящее из всех эле-
ментов множества A, которые не принадлежат множеству B . Приведем некоторые
свойства операций объединения и пересечения множеств и два полезных обозна-
чения: 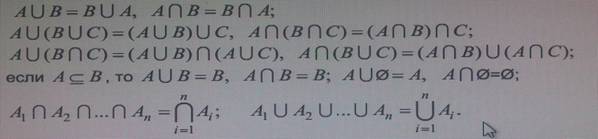
Множество называется конечным, если число его элементов конечно, Множество
называется счетным, если число его элементов бесконечно, но между ними и эле-
ментами множества N можно установить взаимнооднозначное соответствие. В про-
тивном случае бесконечное множество называется несчетным. Счетными множест-
вами являются, например, числовые множества Z и Q , а несчетными – любой ин-
тервал или объединение интервалов и множество R .
Билет №2. Числовая последовательность и её предел.
Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Определение.Пусть каждому натуральному числу n поставлено в соответствие некоторое единственное действительное число 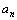 (при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция:
(при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция: 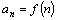 , которая называется числовой последовательностью или просто последовательностью.
, которая называется числовой последовательностью или просто последовательностью.
Последовательность обозначается: 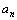 , n=1, 2,… или
, n=1, 2,… или 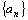 .
.
Числа 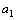 ,
, 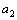 ,… называются членами последовательности или ее элементами,
,… называются членами последовательности или ее элементами, 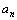 – общим членом последовательности, n – номером члена
– общим членом последовательности, n – номером члена 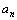 .
.
По определению любая последовательность содержит бесконечное множество элементов.
Часто последовательность задается при помощи формулы: 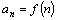 ,
, 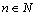 . В этом случае эта формула называется формулой общего члена последовательности {
. В этом случае эта формула называется формулой общего члена последовательности { 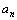 }. Например,
}. Например, 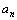 =
= 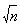 ,
, 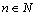 ;
;
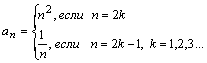
Последовательность может быть задана и другими способами. Например, если 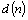 – число всех различных делителей числа n, то
– число всех различных делителей числа n, то 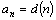 ,
, 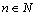 - последовательность, для которой
- последовательность, для которой 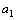 =1,
=1, 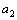 =2,
=2, 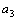 =2,
=2, 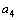 =3,
=3, 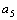 =2,
=2, 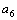 =4,
=4, 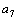 =2,…
=2,…
Для задания последовательностей используют также рекуррентные соотношения. При таком способе задания последовательности указывают один или несколько первых ее членов и формулу, которая позволяет найти ее n-й член через предшествующие члены. Например,
a 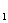 =1, a
=1, a 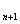 =
= 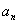 +1 при n=1, 2,…;
+1 при n=1, 2,…;
b 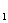 =1, b
=1, b 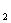 =2, b
=2, b 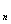 =2b
=2b 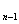 +b
+b 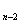 при n
при n 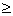 3.
3. 
Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
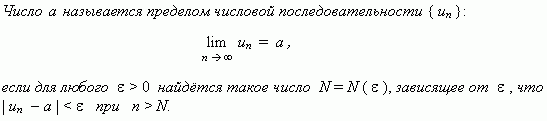
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого 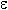 > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала ( a
> 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала ( a 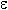 a
a 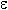 ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что | un | 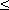 Mдля всех n . Возрастающая или убывающая последовательность называется монотонной.
Mдля всех n . Возрастающая или убывающая последовательность называется монотонной.
Теорема Вейерштрасса.Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства).
Основные свойства пределов.Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.
Если { un } и { vn } две сходящиеся последовательности, то:
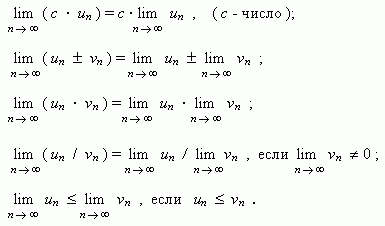
Если члены последовательностей { un }, { vn },{ wn }удовлетворяют неравенствам
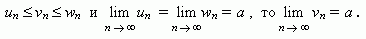
Билет №3. Нахождение предела функции в точке.
Все основывается на определении односторонних пределов. Без вычисления односторонних пределов не обойтись при нахождении вертикальных асимптот графика функции.
Определение (нахождение предела функции слева).
Число В называется пределом функции f(x) слева при 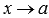 , если для любой сходящейся к а последовательности аргументов функции
, если для любой сходящейся к а последовательности аргументов функции 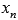 , значения которых остаются меньше а (
, значения которых остаются меньше а ( 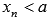 ), последовательность значений этой функции сходится к В.
), последовательность значений этой функции сходится к В.
Обозначается 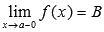 .
.
Определение (нахождение предела функции справа).
Число В называется пределом функции f(x) справа при 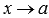 , если для любой сходящейся к а последовательности аргументов функции
, если для любой сходящейся к а последовательности аргументов функции 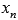 , значения которых остаются больше а (
, значения которых остаются больше а ( 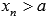 ), последовательность значений этой функции сходится к В.
), последовательность значений этой функции сходится к В.
Обозначается 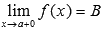 .
.
Определение (существование предела функции в точке).
Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой.
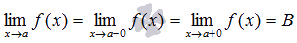
Замечание.
Предел функции f(x) в точке а бесконечен, если пределы слева и справа а бесконечны.
Пример.
Доказать существование конечного предела функции 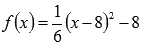 в точке
в точке 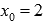 . Найти его значение.
. Найти его значение.
Решение.
Будем отталкиваться от определения существования предела функции в точке.
Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов 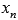 , сходящуюся к
, сходящуюся к 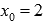 , причем
, причем 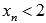 . Примером такой последовательности может являться
. Примером такой последовательности может являться
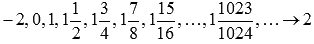
Соответствующая последовательность значений функции будет иметь вид
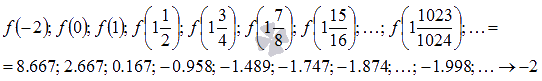
На рисунке соответствующие значения показаны зелеными точками.
Легко видеть, что эта последовательность сходится к -2, поэтому 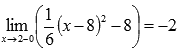 .
.
Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов 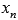 , сходящуюся к
, сходящуюся к 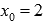 , причем
, причем 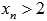 . Примером такой последовательности может являться
. Примером такой последовательности может являться
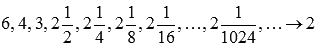
Соответствующая последовательность значений функции будет иметь вид
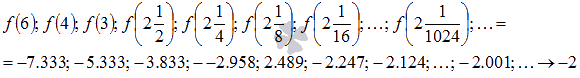
На рисунке соответствующие значения показаны синими точками.
Легко видеть, что эта последовательность также сходится к -2, поэтому 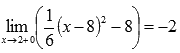 .
.
Этим мы показали, что пределы слева и справа равны, следовательно, по определению существует предел функции 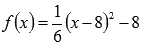 в точке
в точке 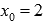 , причем
, причем 
Графическая иллюстрация.
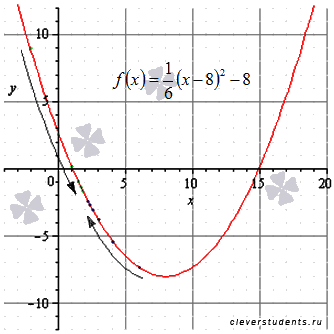
Билет №4. Нахождение предела функции на бесконечности.
Число А называется пределом функции f(x) при 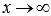 , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается
, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается  .
.
Замечание.
Предел функции f(x) при 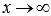 бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается
бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается 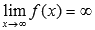 .
.
Билет №5. Основные теоремы о пределах.
Теорема 1. (о предельном переходе в равенстве)Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
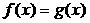 Þ
Þ 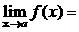
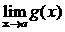 .
.
Теорема 2. (о предельном переходе в неравенстве)Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
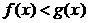 Þ
Þ 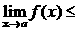
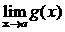 .
.
Теорема 3. Предел постоянной равен самой постоянной.
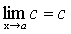 .
.
Доказательство. f(x)=с, докажем, что 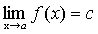 .
.
Возьмем произвольное e>0. В качестве d можно взять любое
положительное число. Тогда при 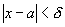
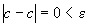 .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
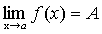 и
и 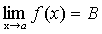 .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A= 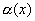 - б.м. при
- б.м. при 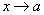 ,
,
f(x)-B= 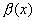 - б.м. при
- б.м. при 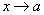 .
.
Вычитая эти равенства, получим: 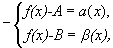
B-A= 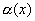 -
- 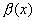 .
.
Переходя к пределам в обеих частях равенства при 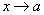 , имеем:
, имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при 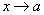 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 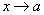 , причем предел алгебраической суммы равен алгебраической сумме пределов.
, причем предел алгебраической суммы равен алгебраической сумме пределов.
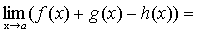
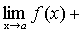
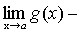
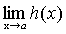 .
.
Доказательство. Пусть 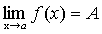 ,
, 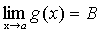 ,
, 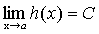 .
.
Тогда, по теореме о связи предела и б.м. функции:
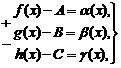 где
где 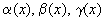 - б.м. при
- б.м. при 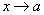 .
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)= 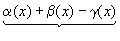 ,
,
где 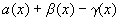 б.м. при
б.м. при 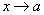 .
.
По теореме о связи предела и б.м. функции:
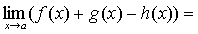 А+В-С=
А+В-С= 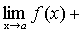
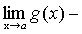
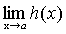 .
.
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при 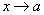 , то и произведение имеет предел при
, то и произведение имеет предел при 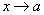 , причем предел произведения равен произведению пределов.
, причем предел произведения равен произведению пределов.
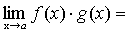
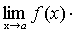
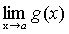 .
.
Следствие. Постоянный множитель можно выносить за знак предела.
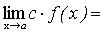
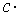
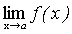 .
.
Теорема 7. Если функции f(x) и g(x) имеют предел при 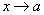 ,
,
причем 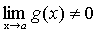 , то и их частное имеет предел при
, то и их частное имеет предел при 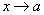 , причем предел частного равен частному пределов.
, причем предел частного равен частному пределов.
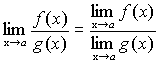 ,
, 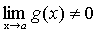 .
.
Билет №6. Первый замечательный предел.
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:
- Первый замечательный предел:
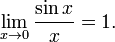
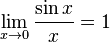
Доказательство
Рассмотрим односторонние пределы 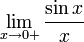 и
и 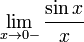 и докажем, что они равны 1.
и докажем, что они равны 1.
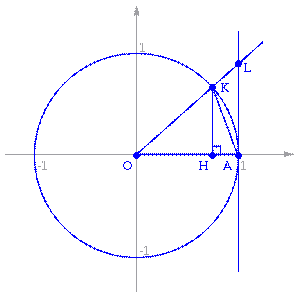
Пусть 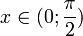 . Отложим этот угол на единичной окружности (
. Отложим этот угол на единичной окружности ( 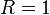 ).
).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке 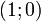 . Точка H — проекция точки K на ось OX.
. Точка H — проекция точки K на ось OX.
Очевидно, что:
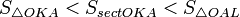 (1)
(1)
(где 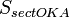 — площадь сектора
— площадь сектора 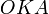 )
)
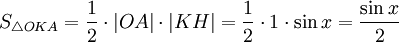
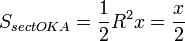
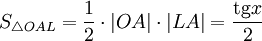
(из 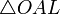 :
: 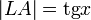 )
)
Подставляя в (1), получим:
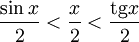
Так как при 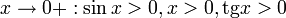 :
:
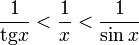
Умножаем на 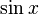 :
:
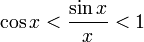
Перейдём к пределу:
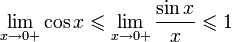
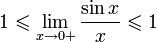
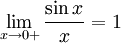
Найдём левый односторонний предел:
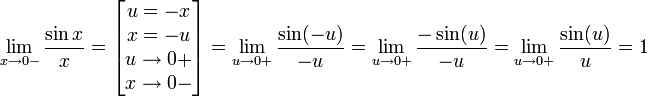
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Доказательства
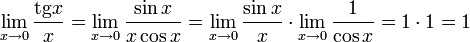
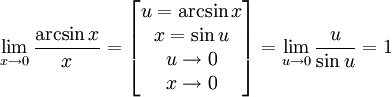
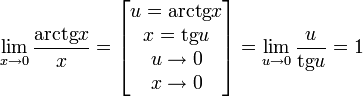
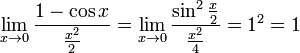
Билет №7. Второй замечательный предел
Справка: 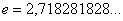 – это иррациональное число.
– это иррациональное число.
имеет вид:
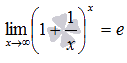
или в другой записи
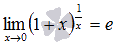
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность 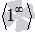 .
.
Разберем несколько примеров нахождения предела по второму замечательному пределу сподробным оприсанием решения.
Пример.
Вычислить предел 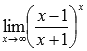
Решение.
Подставляем бесконечность:
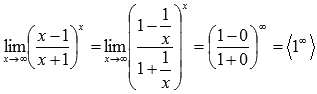
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
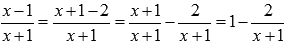
Тогда предел запишется в виде:
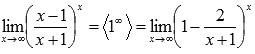
Сделаем замену переменных. Пусть
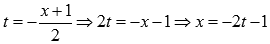
Если 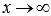 , то
, то 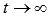
Исходный предел после замены примет вид:
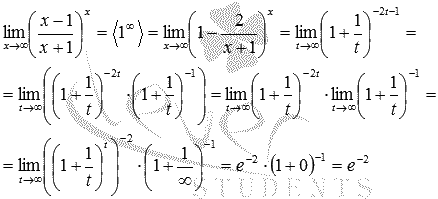
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:
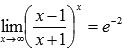
ЗАМЕЧАНИЕНеопределнность единица в степени бесконечность 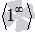 является степенной неопределенностью, так что может быть раскрыта по правилам нахождения пределов показательно степенных функций.
является степенной неопределенностью, так что может быть раскрыта по правилам нахождения пределов показательно степенных функций.
Билет №8. Бесконечно малые функции. Сравнение бесконечно малых функций
Функция α (x) называется бесконечно малой при 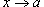 , если
, если

Предположим, что α (x) и β (x) - бесконечно малые функции при 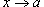 .
.
· Если 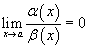 , то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);
, то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);
· Если 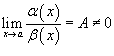 , то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;
, то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;
· Если 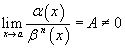 , то говорят, что функция α (x) является бесконечно малой порядка относительно функции β (x);
, то говорят, что функция α (x) является бесконечно малой порядка относительно функции β (x);
· Если 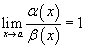 , то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при
, то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при 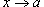 .
.
Билет №9. Таблица эквивалентных бесконечно малых функций
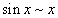 | 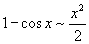 |
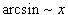 | 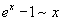 |
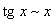 | 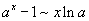 |
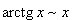 | 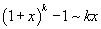 |
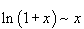 | 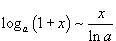 |
Билет №10. Бесконечно большие функции. Сравнение бесконечно больших функций.
А) Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Бесконечно большая величина
Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция 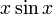 , неограниченная с обеих сторон, не является бесконечно большой при
, неограниченная с обеих сторон, не является бесконечно большой при 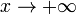 .
.
Последовательность 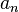 называется бесконечно большой, если
называется бесконечно большой, если 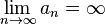 .
.
Функция называется бесконечно большой в окрестности точки 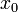 , если
, если 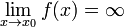 .
.
Функция называется бесконечно большой на бесконечности, если 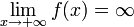 либо
либо 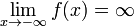 .
.
| б) Сравнение бесконечно больших | |
Пусть 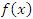 и и 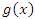 – бесконечно большие функции при x → a. Рассмотрим возможные значения предела отношения этих функций: – бесконечно большие функции при x → a. Рассмотрим возможные значения предела отношения этих функций: 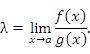 Если Если 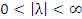 , то функции , то функции 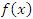 и и 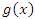 называются бесконечно большими одного и того же порядка. Функции называются бесконечно большими одного и того же порядка. Функции 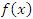 и и 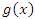 называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида 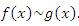 Функция Функция 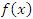 называется бесконечно большой более высокого порядка по сравнению с называется бесконечно большой более высокого порядка по сравнению с 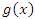 при x → a, если λ = ∞; при этом говорят, что при x → a, если λ = ∞; при этом говорят, что 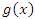 имеет меньший порядок роста. Если имеет меньший порядок роста. Если 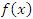 и и 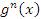 представляют собой бесконечно большие функции одного и того же порядка, то функция представляют собой бесконечно большие функции одного и того же порядка, то функция 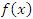 называется бесконечно большой n-го порядка по сравнению с называется бесконечно большой n-го порядка по сравнению с 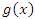 . Например, функция . Например, функция 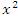 является бесконечно большой 4-го порядка по сравнению с является бесконечно большой 4-го порядка по сравнению с 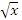 при x → ∞. Если λ = 0, то бесконечно большие функции при x → ∞. Если λ = 0, то бесконечно большие функции 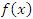 и и 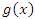 меняются своими ролями. В этом случае функция меняются своими ролями. В этом случае функция 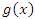 является бесконечно большой более высокого порядка по сравнению с является бесконечно большой более высокого порядка по сравнению с 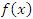 при x → a. Свойства эквивалентных бесконечно больших функций. Если при x → a. Свойства эквивалентных бесконечно больших функций. Если 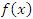 и и 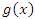 – эквивалентные бесконечно большие функции при x → a, то их разность имеет меньший порядок роста. Действительно, – эквивалентные бесконечно большие функции при x → a, то их разность имеет меньший порядок роста. Действительно, 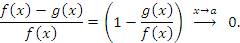 Если Если 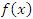 и и 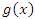 – бесконечно большие функции одного и того же порядка при x → a, то – бесконечно большие функции одного и того же порядка при x → a, то 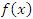 и и 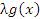 являются эквивалентными бесконечно большими функциями: являются эквивалентными бесконечно большими функциями: 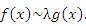 Иначе говоря, бесконечно большие функции Иначе говоря, бесконечно большие функции 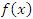 и и 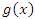 асимптотически пропорциональны при x → a. Если бесконечно малая асимптотически пропорциональны при x → a. Если бесконечно малая 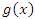 имеет меньший порядок роста по сравнению с имеет меньший порядок роста по сравнению с 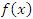 при x → a, то при x → a, то 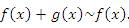 В таких случаях говорят, что В таких случаях говорят, что 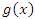 – пренебрежимо малая величина по сравнению с – пренебрежимо малая величина по сравнению с 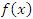 . в) Функция . в) Функция 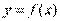 называется бесконечно малой при называется бесконечно малой при 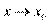 , если , если 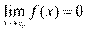 . Функция . Функция 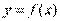 называется бесконечно большой при называется бесконечно большой при 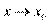 , если для любого положительного числа , если для любого положительного числа 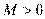 существует такое число существует такое число 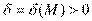 , что для всех , что для всех 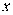 , удовлетворяющих неравенству , удовлетворяющих неравенству 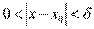 , выполняется неравенство , выполняется неравенство 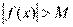 . Записывается: . Записывается: 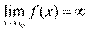 . Свойства бесконечно малых функций: 1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. 2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. 3)Произведение двух бесконечно малых функций есть функция бесконечно малая. 4)Произведение бесконечно малой функции на число есть функция бесконечно малая. 5)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая. Теорема о связи между бесконечно большой и бесконечно малой функциями: Если функция . Свойства бесконечно малых функций: 1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. 2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. 3)Произведение двух бесконечно малых функций есть функция бесконечно малая. 4)Произведение бесконечно малой функции на число есть функция бесконечно малая. 5)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая. Теорема о связи между бесконечно большой и бесконечно малой функциями: Если функция 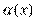 - функция бесконечно малая ( - функция бесконечно малая ( 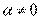 ), то функция ), то функция 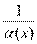 есть бесконечно большая функция и наоборот. Доказательство: Пусть есть бесконечно большая функция и наоборот. Доказательство: Пусть 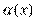 - бесконечно малая функция при - бесконечно малая функция при 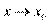 , т.е. , т.е. 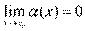 . Тогда для любого числа . Тогда для любого числа 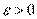 существует такое число существует такое число 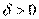 , что для всех , что для всех 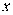 , удовлетворяющих неравенству , удовлетворяющих неравенству 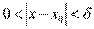 , выполняется неравенство , выполняется неравенство 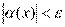 , т.е. , т.е. 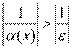 , т.е. , т.е. 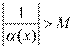 , где , где 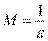 . А из этого следует, что функция . А из этого следует, что функция 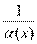 - бесконечно большая. Билет №11. Непрерывность функции в точке и области, нарушения непрерывности, точки разрыва и их классификация. - бесконечно большая. Билет №11. Непрерывность функции в точке и области, нарушения непрерывности, точки разрыва и их классификация.     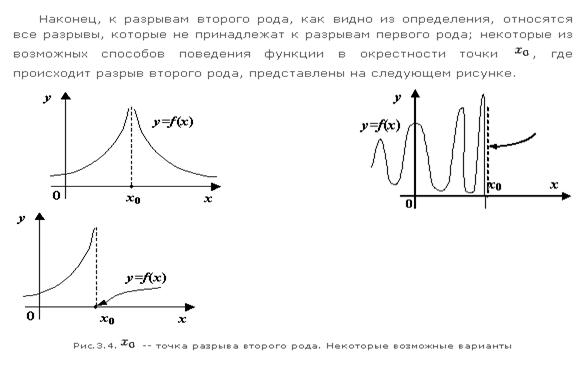  Билет №12. Производная функции, ее механический и геометрический смысл. Билет №12. Производная функции, ее механический и геометрический смысл. 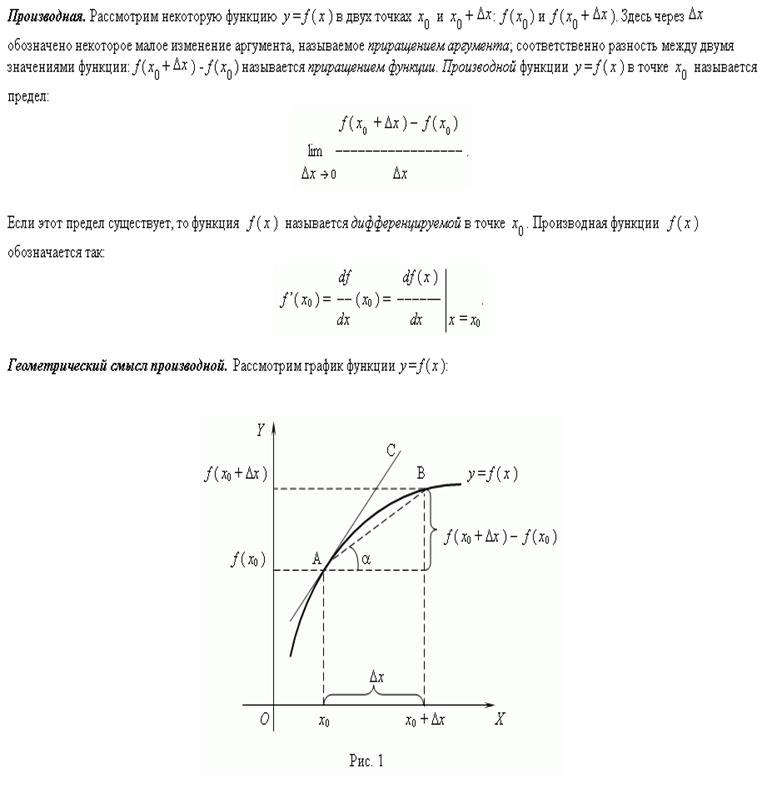  |
Билет №13. Правила дифференцирования.
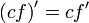
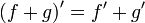
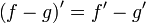
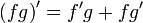 (частный случай формулы Лейбница)
(частный случай формулы Лейбница)
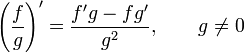
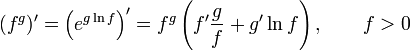
Билет №14.Таблица основных производных.
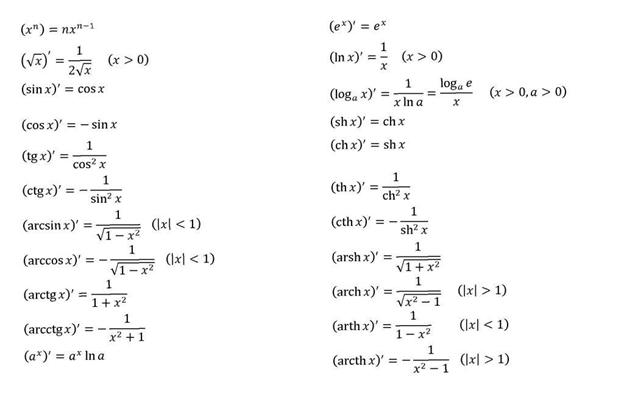
Тут, начиная с 4 в правом столбце, нам не нужно))
Дифференциал функции
Функция 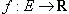 называется дифференцируемой в точке
называется дифференцируемой в точке 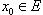 , предельной для множества E, если ее приращение Δf(x0), соответствующее приращению аргумента x, может быть представлено в виде
, предельной для множества E, если ее приращение Δf(x0), соответствующее приращению аргумента x, может быть представлено в виде
Δf(x0) = A(x0)(x - x0) + ω(x - x0), (1)
где ω(x - x0) = о(x - x0) при x → x0.
Отображение 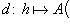
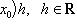 , называется дифференциалом функции f в точке x0, а величина A(x0)h - значением дифференциала в этой точке.
, называется дифференциалом функции f в точке x0, а величина A(x0)h - значением дифференциала в этой точке.
Для значения дифференциала функции f принято обозначение df или df(x0), если требуется знать, в какой именно точке он вычислен. Таким образом,
df(x0) = A(x0)h.
Разделив в (1) на x - x0 и устремив x к x0, получим A(x0) = f'(x0). Поэтому 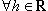 имеем
имеем
df(x0) = f'(x0)h. (2)
Сопоставив (1) и (2), видим, что значение дифференциала df(x0) (при f'(x0) ≠ 0) есть главная часть приращения функции f в точке x0, линейная и однородная в то же время относительно приращения h = x - x0.
Инвариантность формы первого дифференциала
Если x - независимая переменная, то dx = x - x0 (фиксированное приращение). В этом случае имеем
df(x0) = f'(x0)dx. (3)
Если x = φ(t) - дифференцируемая функция, то dx = φ'(t0)dt. Следовательно,
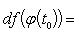
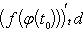
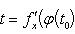
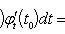
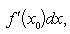
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.
Билет №20. Производные и дифференциалы высших порядков.
Производной n-го порядка f(n)(x) называется производная от производной (n-1)-го порядка:
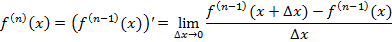
Дифференциалом n-го порядка dny называется дифференциал от дифференциала (n-1)-го порядка как функции x:
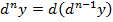
Билет №21. Уравнение касательной и нормали к кривой.
Уравнение касательной к графику функции y = f(x) в точке x0 равно:
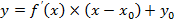
Нормалью к кривой называется прямая, перпендикулярная касательной и проходящая через точку касания:
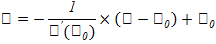
Билет № 22. Теорема Ролля
Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.