Наибольшее и наименьшее значения функции двух переменных в замкнутой области

Теорема 1.5 Пусть в замкнутой области D задана функцияz=z(x,y), имеющая непрерывные частные производные первого порядка. Граница Г области D является кусочно гладкой (т. е. состоит из кусков "гладких на ощупь" кривых или прямых). Тогда в области D функция z(x,y) достигает своего наибольшего M и наименьшего m значений.

Без доказательства.

Можно предложить следующий план нахождения M и m.
1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы.
2. Находим стационарные точки внутри D.
3. Находим стационарные точки на каждой из границ.
4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения.

Пример 1.14 Найти наибольшее M и наименьшее m значения функции z= 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x= 0, y = 0, 4x+3y=12 .

Решение

1. Построим область D (рис. 1.5) на плоскости Оху.

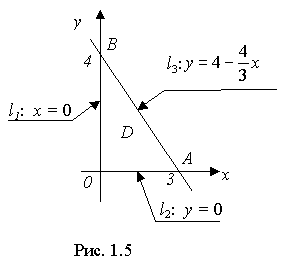
Угловые точки: О (0; 0), В (0; 4), А (3; 0).

Граница Г области D состоит из трёх частей:

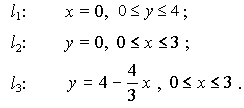
2. Найдём стационарные точки внутри области D:

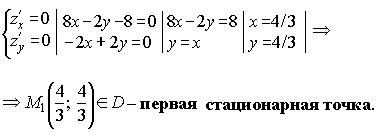
3. Стационарные точки на границах l₁, l₂, l₃:

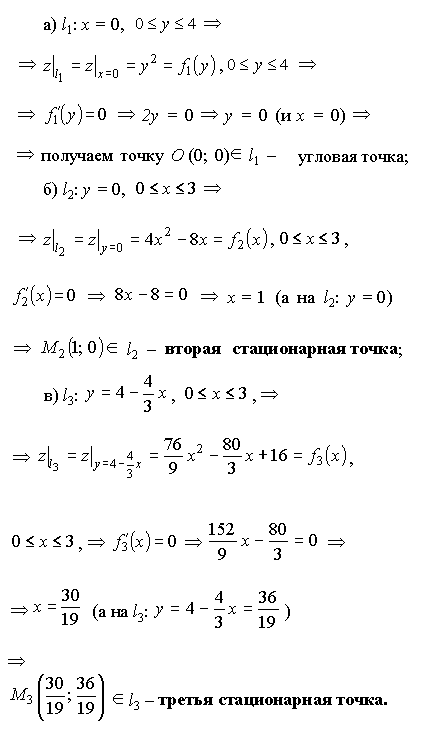
4. Вычисляем шесть значений:

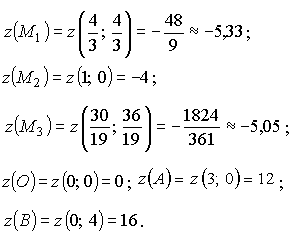
Из полученных шести значений выбираем наибольшее и наименьшее.

Ответ:

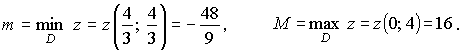
Примеры

Пример 1.

Исследовать на непрерывность функцию

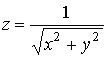
Решение

Данная функция определена при всех значениях переменных x и y, кроме начала координат, где знаменатель обращается в нуль.

Многочлен x²+y² непрерывен всюду, а значит и непрерывен корень квадратный из непрерывной функции.

Дробь же будет непрерывной всюду, кроме точек, где знаменатель равен нулю. То есть рассматриваемая функция непрерывна на всей координатной плоскости Оху, исключая начало координат.

Пример 2.

Исследовать на непрерывность функцию z=tg(x,y). Тангенс определен и непрерывен при всех конечных значениях аргумента, кроме значений, равных нечетному числу величины π/2, т.е. исключая точки, где

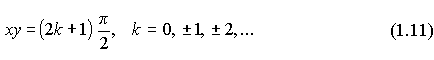
При каждом фиксированном "k" уравнение (1.11) определяет гиперболу. Поэтому рассматриваемая функция является непрерывной функцией xи y, исключая точки, лежащие на кривых (1.11).

Пример 3.

Найти частные производные функции u=z^-xy, z > 0.

Решение

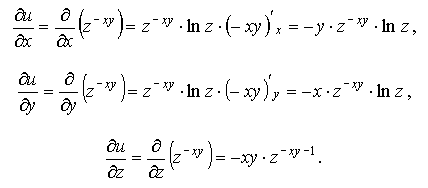
Пример 4.

Показать, что функция

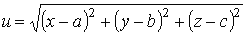
удовлетворяет тождеству:

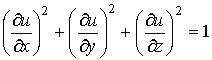
Решение

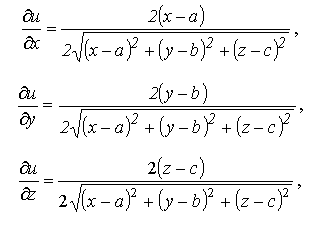
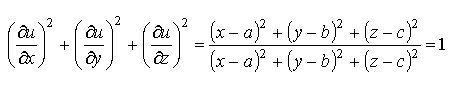
– данное равенство справедливо для всех точек М(х;у;z), кроме точки М₀(a;b;c).

Рассмотрим функцию z=f(х,у) двух независимых переменных и установим геометрический смысл частных переменных z'_x=f'_x(х,у) и z'_y=f'_y(х,у).

В этом случае уравнение z=f(х,у) есть уравнение некоторой поверхности (рис.1.3). Проведем плоскость y= const. В сечении этой плоскостью поверхности z=f(х,у) получится некоторая линия l₁ пересечения, вдоль которой изменяются лишь величины х и z.

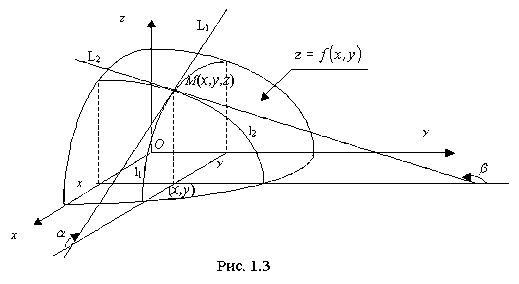
Частная производная z'_x (её геометрический смысл непосредственно следует из известного нам геометрического смысла производной функции одной переменной) численно равна тангенсу угла α наклона, по отношению к оси Ох , касательной L₁ к кривой l₁, получающейся в сечении поверхности z=f(х,у) плоскостью y= const в точке М(х,у,f(xy)): z'_x= tgα.

В сечении же поверхности z=f(х,у) плоскостью х= const получится линия пересечения l₂, вдоль которой изменяются лишь величины у и z. Тогда частная производная z'_y численно равна тангенсу угла β наклона по отношению к оси Оу, касательной L₂ к указанной линии l₂ пересечения в точке М(х,у,f(xy)): z'_x= tgβ.

Пример 5.

Какой угол образует с осью Ох касательная к линии:

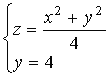
в точке М(2,4,5)?

Решение

Используем геометрический смысл частной производной по переменной х (при постоянном у):

Пример 6.

Дано:

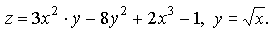
Найти

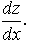
Решение

Согласно (1.31):

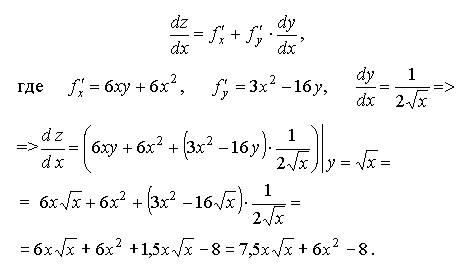
Ответ:

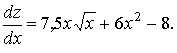
Пример 7.

Считая, что уравнение

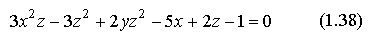
неявно задаёт функцию

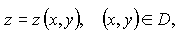
найти z'_x, z'_y.

Решение

Имеем:

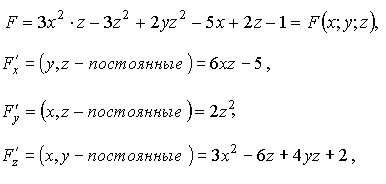
поэтому согласно (1.37) получаем ответ.

Ответ.

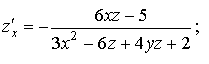
Пример 8.

Исследовать на экстремум:

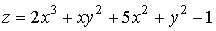
Решение

1. Найдём стационарные точки, решая систему (1.41):

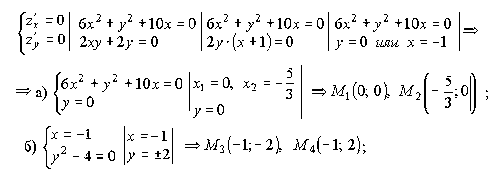
то есть найдены четыре стационарные точки.
2.

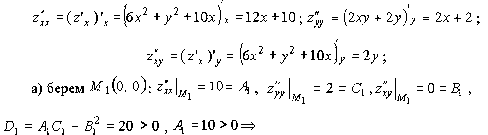
по теореме 1.4 в точке 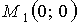– минимум.

Причём

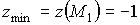
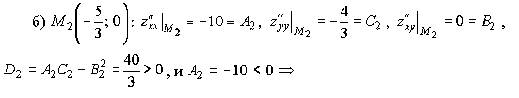
по теореме 1.4 в точке

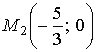
- максимум.
Причём

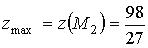
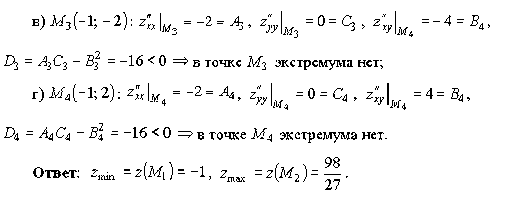
Пример 9.

Найти наибольшее M и наименьшее m значения функции z= 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x= 0, y = 0, 4x+3y=12 .

Решение

1. Построим область D (рис. 1.5) на плоскости Оху.

Угловые точки: О (0; 0), В (0; 4), А (3; 0).

Граница Г области D состоит из трёх частей:

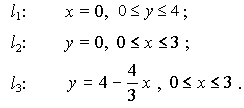
2. Найдём стационарные точки внутри области D:

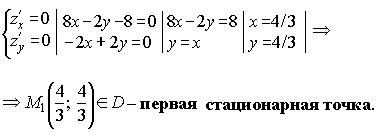
3. Стационарные точки на границах l₁, l₂, l₃:

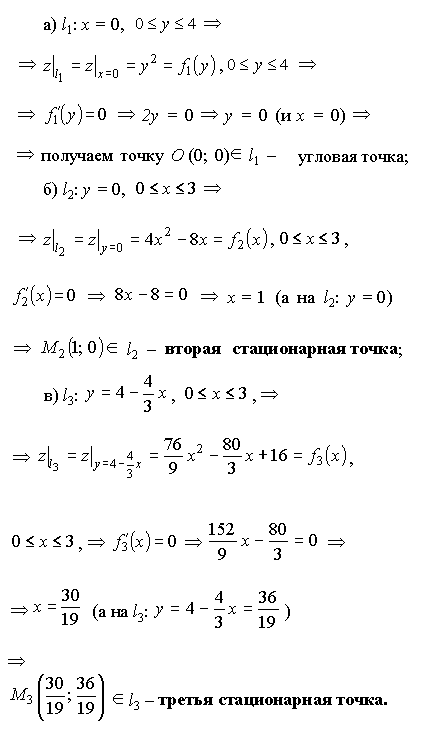
4. Вычисляем шесть значений:

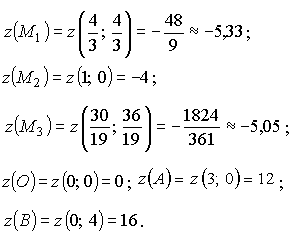
Из полученных шести значений выбираем наибольшее и наименьшее.

Ответ:

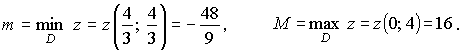
Список литературы:

ü Белько И. В., Кузьмич К. К. Высшая математика для экономистов. I семестр: Экспресс-курс. – М.: Новое знание, 2002. – 140 с.

ü Гусак А. А.. Математический анализ и дифференциальные уравне-ния.– Мн.: ТетраСистемс, 1998. – 416 с.

ü Гусак А. А.. Высшая математика. Учебное пособие для студентов вузов в 2-х томах. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).

ü Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.

ü Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000. – 351 с.