Определение функции нескольких переменных

Предел функции двух переменных

Рассмотрим плоскость и систему Oxy декартовых прямоугольных координат на ней (можно рассматривать и другие системы координат).

Из аналитической геометрии знаем, что каждой упорядоченной паре чисел ( x, y ) можно сопоставить единственную точку M плоскости и наоборот, каждой точке M плоскости соответствует единственная пара чисел.

Поэтому в дальнейшем, говоря о точке, мы будем часто подразумевать соответствующую ей пару чисел ( x, y ) и наоборот.

Определение 1.2 Множество пар чисел ( x, y ), удовлетворяющих неравенствам, называется прямоугольником (открытым).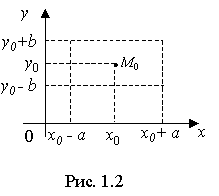

На плоскости он изобразится прямоугольником (рис. 1.2) со сторонами, параллельными осям координат, и с центром в точке M₀(x₀y₀).

Прямоугольник принято обозначать следующим символом:

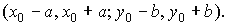
Введем важное для дальнейшего изложения понятие: окрестность точки.

Определение 1.3 Прямоугольной δ-окрестностью (дельта-окрестностью) точки
M₀(x₀y₀) называется прямоугольник

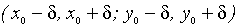
с центром в точке M₀ и с одинаковыми по длине сторонами 2δ.

Определение 1.4 Круговой δ - окрестностью точки M₀(x₀y₀) называется круг радиуса δ с центром в точке M₀, т. е. множество точек M(xy), координаты которых удовлетворяют неравенству:

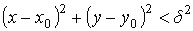
Можно ввести понятия окрестностей и других видов, но для целей математического анализа технических задач, в основном, используются лишь прямоугольные и круговые окрестности.

Введём следующее понятие предела функции двух переменных.

Пусть функция z= f ( x, y ) определена в некоторой области ζ и M₀(x₀y₀) - точка, лежащая внутри или на границе этой области.

Определение 1.5Конечное число A называется пределом функции f ( x, y ) пр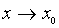и

и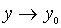

если для любого положительного числа ε можно найти такое положительное число δ, что неравенство

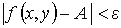
выполняется для всех точек М(х,у) из области ζ, отличных от M₀(x₀y₀), координаты которых удовлетворяют неравенствам:

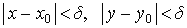
Смысл этого определения состоит в том, что значения функции f( х, у ) как угодно мало отличаются от числа А в точках достаточно малой окрестности точки М₀.

Здесь в основу определения положены прямоугольные окрестности М₀. Можно было бы рассматривать круговые окрестности точки М₀ и тогда нужно было бы требовать выполнения неравенства

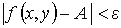
во всех точках М(х,у) области ζ, отличных от М₀ и удовлетворяющих условию:

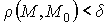
где

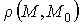
- расстояние между точками М и М₀.

Употребительны следующие обозначения предела:

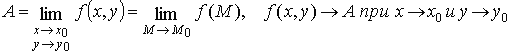
Учитывая определение предела функции двух переменных, можно перенести основные теоремы о пределах для функций одной переменной на функции двух переменных.

Например, теоремы о пределе суммы, произведения и частного двух функций.

Примеры

Пример 1.

Исследовать на непрерывность функцию

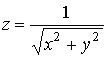
Решение

Данная функция определена при всех значениях переменных x и y, кроме начала координат, где знаменатель обращается в нуль.

Многочлен x²+y² непрерывен всюду, а значит и непрерывен корень квадратный из непрерывной функции.

Дробь же будет непрерывной всюду, кроме точек, где знаменатель равен нулю. То есть рассматриваемая функция непрерывна на всей координатной плоскости Оху, исключая начало координат.

Пример 2.

Исследовать на непрерывность функцию z=tg(x,y). Тангенс определен и непрерывен при всех конечных значениях аргумента, кроме значений, равных нечетному числу величины π/2, т.е. исключая точки, где

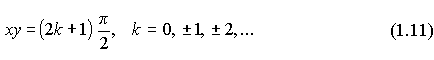
При каждом фиксированном "k" уравнение (1.11) определяет гиперболу. Поэтому рассматриваемая функция является непрерывной функцией xи y, исключая точки, лежащие на кривых (1.11).

Пример 3.

Найти частные производные функции u=z^-xy, z > 0.

Решение

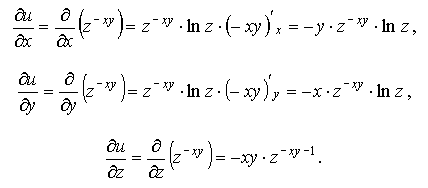
Пример 4.

Показать, что функция

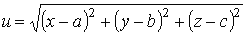
удовлетворяет тождеству:

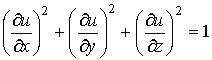
Решение

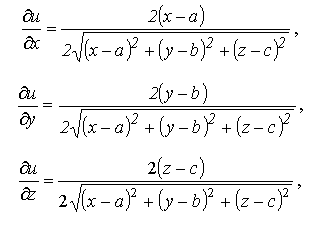
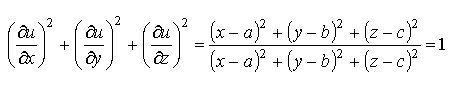
– данное равенство справедливо для всех точек М(х;у;z), кроме точки М₀(a;b;c).

Рассмотрим функцию z=f(х,у) двух независимых переменных и установим геометрический смысл частных переменных z'_x=f'_x(х,у) и z'_y=f'_y(х,у).

В этом случае уравнение z=f(х,у) есть уравнение некоторой поверхности (рис.1.3). Проведем плоскость y= const. В сечении этой плоскостью поверхности z=f(х,у) получится некоторая линия l₁ пересечения, вдоль которой изменяются лишь величины х и z.

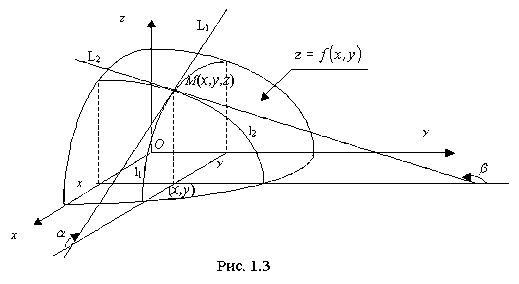
Частная производная z'_x (её геометрический смысл непосредственно следует из известного нам геометрического смысла производной функции одной переменной) численно равна тангенсу угла α наклона, по отношению к оси Ох , касательной L₁ к кривой l₁, получающейся в сечении поверхности z=f(х,у) плоскостью y= const в точке М(х,у,f(xy)): z'_x= tgα.

В сечении же поверхности z=f(х,у) плоскостью х= const получится линия пересечения l₂, вдоль которой изменяются лишь величины у и z. Тогда частная производная z'_y численно равна тангенсу угла β наклона по отношению к оси Оу, касательной L₂ к указанной линии l₂ пересечения в точке М(х,у,f(xy)): z'_x= tgβ.

Пример 5.

Какой угол образует с осью Ох касательная к линии:

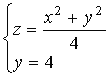
в точке М(2,4,5)?

Решение

Используем геометрический смысл частной производной по переменной х (при постоянном у):

Пример 6.

Дано:

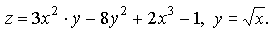
Найти

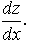
Решение

Согласно (1.31):

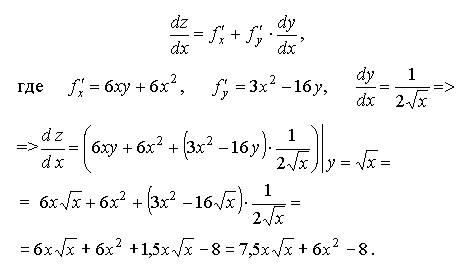
Ответ:

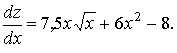
Пример 7.

Считая, что уравнение

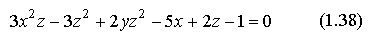
неявно задаёт функцию

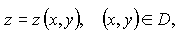
найти z'_x, z'_y.

Решение

Имеем:

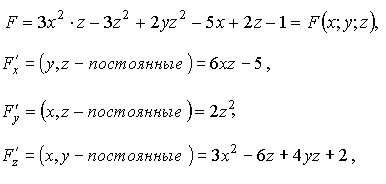
поэтому согласно (1.37) получаем ответ.

Ответ.

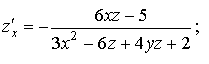
Пример 8.

Исследовать на экстремум:

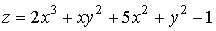
Решение

1. Найдём стационарные точки, решая систему (1.41):

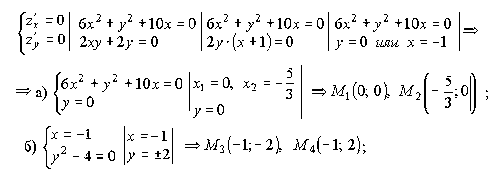
то есть найдены четыре стационарные точки.
2.

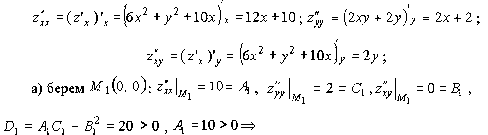
по теореме 1.4 в точке 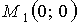– минимум.

Причём

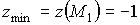
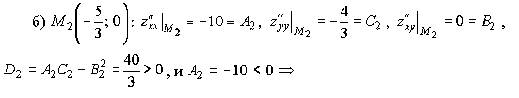
по теореме 1.4 в точке

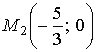
- максимум.
Причём

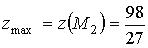
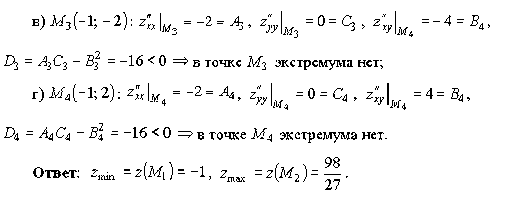
Пример 9.

Найти наибольшее M и наименьшее m значения функции z= 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x= 0, y = 0, 4x+3y=12 .

Решение

1. Построим область D (рис. 1.5) на плоскости Оху.

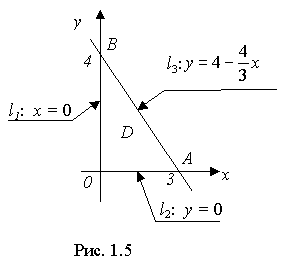
Угловые точки: О (0; 0), В (0; 4), А (3; 0).

Граница Г области D состоит из трёх частей:

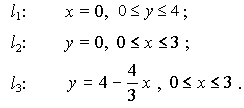
2. Найдём стационарные точки внутри области D:

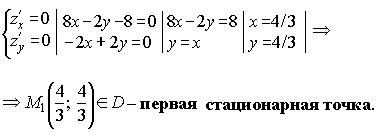
3. Стационарные точки на границах l₁, l₂, l₃:

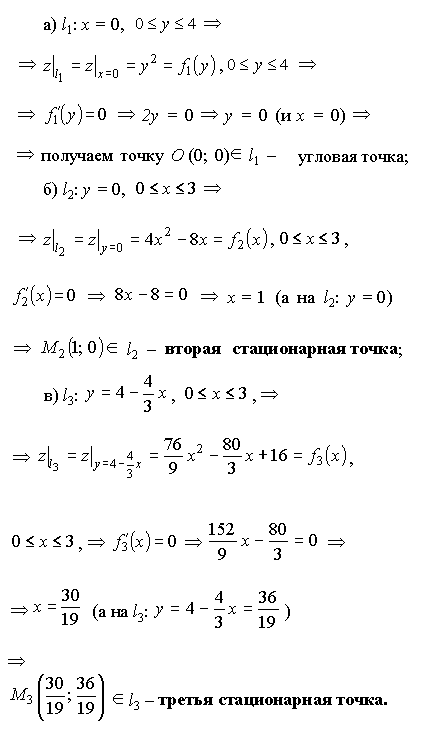
4. Вычисляем шесть значений:

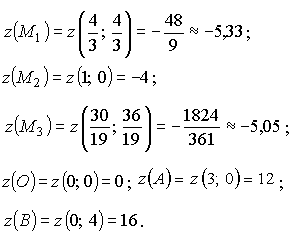
Из полученных шести значений выбираем наибольшее и наименьшее.

Ответ:

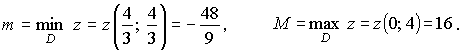
Список литературы:

ü Белько И. В., Кузьмич К. К. Высшая математика для экономистов. I семестр: Экспресс-курс. – М.: Новое знание, 2002. – 140 с.

ü Гусак А. А.. Математический анализ и дифференциальные уравне-ния.– Мн.: ТетраСистемс, 1998. – 416 с.

ü Гусак А. А.. Высшая математика. Учебное пособие для студентов вузов в 2-х томах. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).

ü Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.

ü Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000. – 351 с.

Определение функции нескольких переменных

При рассмотрении многих вопросов из различных областей знания приходится изучать такие зависимости между переменными величинами, когда числовые значения одной из них полностью определяются значениями нескольких других.

Например, изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами: x, y, z. Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных: x, y, z. Если физическое состояние тела к тому же еще и меняется с течением времени t, то та же плотность будет зависеть уже от значений четырех переменных: x, y, z, t.

Другой пример: изучаются издержки производства на изготовление единицы некоторого вида продукции. Пусть:
x - затраты по материалам,
y - расходы на выплату заработной платы работникам,
z - амортизационные отчисления.
Очевидно, что издержки производства зависят от значений названных параметров x, y, z.

Определение 1.1 Если каждой совокупности значений "n" переменных

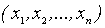
из некоторого множества D этих совокупностей соответствует своё единственное значение переменной z, то говорят, что на множестве D задана функция

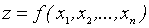
"n" переменных.

Множество D, указанное в определении 1.1, называется областью определяния или областью существования этой функции.

Если рассматривается функция двух переменных, то совокупности чисел

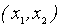
обозначаются, как правило, (x, y) и интерпретируются как точки координатной плоскости Oxy, а область определения функции z= f ( x, y ) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy.

Так, например, областью определения функции

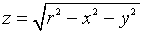
является множество точек плоскости Oxy, координаты которых удовлетворяют соотношению

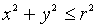
т. е. представляет собой круг радиуса r с центром в начале координат.

Для функции

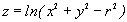
областью определения служат точки, которые удовлетворяют условию

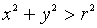
т. е. внешние по отношению к заданному кругу.

Часто функции двух переменных задаются в неявном виде, т. е. как уравнение

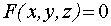
связывающее три переменные величины. В этом случае каждую из величин x, y, z можно рассматривать как неявную функцию двух остальных.

Геометрическим изображением (графиком) функции двух переменных z= f ( x, y ) является множество точек P ( x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z= f ( x, y ).

Графиком функции непрерывных аргументов, как правило, является некоторая поверхность в пространстве Oxyz, которая проектируется на координатную плоскость Oxy в область определения функции z=f ( x, y ).

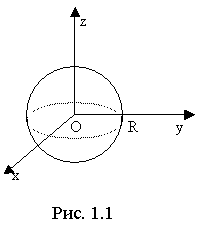
Так, например, (рис. 1.1) графиком функции

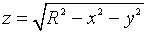
является верхняя половина сферы, а графиком функции

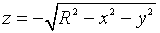
- нижняя половина сферы.

Графиком линейной функции z= ax + by + сявляется плоскость в пространстве Oxyz, а графиком функции z= сonst служит плоскость, параллельная координатной плоскости Oxyz.

Заметим, что функцию трех и большего числа переменных изобразить наглядно в виде графика в трехмерном пространстве невозможно.

В дальнейшем будем в основном ограничиваться рассмотрением функций двух или трех переменных, так как рассмотрение случая большего (но конечного) числа переменных производится аналогично.