Модуль 1. Модуль 1. Численные методы решения нелинейных уравнений. Нахождение арифметического корня натуральной степени с заданной точностью.

Модуль 1. Модуль 1. Численные методы решения нелинейных уравнений. Нахождение арифметического корня натуральной степени с заданной точностью.

Численные методы решения нелинейных уравнений.

Постановка задачи.

Этапы приближенного решения нелинейных уравнений.

Уточнение корней методом деления отрезка пополам.

Уточнение корней методом касательных.

Уточнение корней методом хорд.

Нахождение арифметического корня натуральной степени с заданной точностью.

3. Практикум.

Литература.

Численные методы решения нелинейных уравнений.

Постановка задачи.

Пусть имеется уравнение вида

f (x) = 0. (1)

где f (x) - заданная алгебраическая или трансцендентная функция. (Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций - показательная, логарифмическая, тригонометрические, обратные тригонометрические.)

Решить уравнение - значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество, или доказать, что корней нет.

Если алгебраическое или трансцендентное уравнение достаточно сложно, то довольно редко удается точно найти его корни. Кроме того, в некоторых случаях уравнение может содержать коэффициенты, известные лишь приблизительно, поэтому сама задача о точном нахождении корней теряет смысл. В таких случаях применяют численные (приближенные) методы решения.

Поставим задачу найти такое приближенное значение корня x_пр, которое мало отличается от точного значения корня x*, так что выполняется неравенство │x* – x_пр │< e , где e (эпсилон) – малая положительная величина – допустимая ошибка, которую мы можем заранее задать по своему усмотрению. Если корень найден с точностью e, то принято писать x* = x_пр ± e.

Будем предполагать, что уравнение (1) имеет лишь изолированные корни, т.е. для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Уточнение корней методом деления отрезка пополам.

Метод деления отрезка пополам имеет другие названия: метод половинного деления, метод дихотомии, метод проб, метод бисекций.

Пусть корень уравнения f (x) = 0 отделен на отрезке 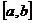, т.е. .

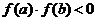Уточнение корней методом касательных.

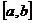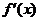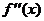Пусть корень уравнения f (x) = 0 отделен на отрезке . Необходимым условием сходимости метода является то, что производные и непрерывны и сохраняют постоянные знаки.

Уточнение корней методом хорд.

Пусть на отрезке 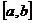функция непрерывна, принимает на концах отрезка значение разных знаков, а производная 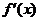сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 10).

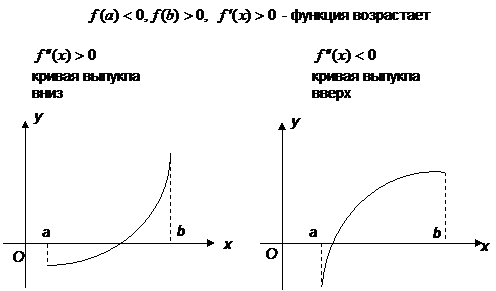
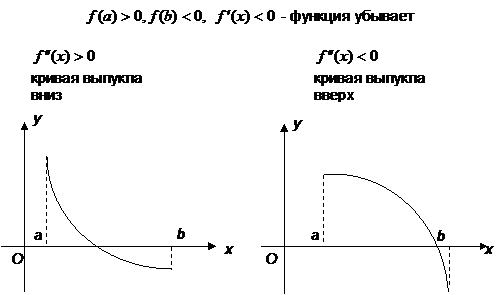
Рис. 10. Возможные случаи расположения кривых.

Практикум.

Ответы.

a, c	a, b, d	d, e, f

c	b	d	b	c	a	d	b	a	c

3,239	[3,2; 3,35]

Литература.

1. Бабаева Н.С. Приближенные методы решения уравнений // Информатика и образование. 2003. № 6.
2. Бахвалов Н.С. Численные методы. – М.: Наука, 1975.
3. Воробьева Г.Н., Данилова А.Н. Практикум по численным методам. – М.: Высш. шк., 1979.
4. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970.
5. Калиткин Н.Н. Численные методы. – М.: Наука, 1978.
6. Корнилов В.С. Как ЭВМ вычисляет квадратный корень. / «В мир информатики» № 36 («Информатика» № 10 / 2004).
7. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1969.
8. Тимофеева Л.А. Численные методы решения задач на ЭВМ // Информатика и образование. 2003. № 12.
9. Турчак Л.И. Основы численных методов. – М.: Высш. шк., 1985.

Модуль 1. Модуль 1. Численные методы решения нелинейных уравнений. Нахождение арифметического корня натуральной степени с заданной точностью.