Вашему вниманию предлагается курс лекций и

Доц.Богданова М.В.

Уважаемые студенты!

Вашему вниманию предлагается курс лекций и

содержание практических занятий, после изучения

Которых Вам будет необходимо сдать зачет, содер жащий 1 теоретический вопрос из лекций и 1 задача

Из практического курса.

Удачи Вам в изучении данного предмета!

Понятие модели, виды моделей

Модель – схематическое представление того или иного предмета, с помощью выбранных средств моделирования.

Модель отражает основную структуру предмета и его свойства, существует большое количество классификаций моделей.

Модель – абстрактный образ объекта или явления и отношений между отдельными частями объекта или явления.

Любая модель это некоторая абстракция, звено в цепочке познания от опыта к абстракции, к осмыслению. Когда осмыслили снова опыту, к практике.

Процесс создания модели называется моделированием.

Существует несколько распространенных видов классификаций моделей определяющихся следующими принципами:

1) областью использования (учебные модели, опытные модели, научно-технические модели, игровые модели);

2) с учетом моделью временного фактора (статические и динамические модели);

3) отрасль знаний (экономика, история, биология и др.);

4) способ представления модели (материальные и абстрактные модели).

Учебные модели используются в процессе обучения – это обучающие программы, различные тренажеры, наглядные пособия.

Опытные модели – уменьшенные или увеличенные копии объекта, используемые для подробного исследования объекта и прогнозирования его будущих характеристик. Например: модель самолета, которая подвергается воздействию в аэродинамической трубе.

Научно-технические модели созданы для исследования процессов. К таким моделям можно отнести стенд для проверки работы схем, транзисторов и т. д..

Игровые модели – деловые, спортивные, экономические, военные и т. п. игры.

С помощью этих моделей можно разрешать конфликтные ситуации, оказывать психологическую помощь.

Имитационная модель –не просто отражает реальность с той или иной степенью точности, а имитирует ее.

Статическая модель – это единовременный срез информации по данному объекту.

Динамическая модель представляет собой картину изменения объекта во времени.

Материальные модели всегда имеют реальное воплощение и могут отражать:

1) внешние свойства исходных объектов;

2) внутренние устройства исходных объектов;

3) суть процессов и явлений происходящих с объектами оригинала. (Примеры: скелет, чучело, робот).

Абстрактная модель не имеет естественного воплощения, основу этой модели составляет информация, она делится на мысленную и вербальную.

Мысленная модель возникает в процессе любой созидательной деятельности человека.

Вербальную модель человек использует для передачи своих мыслей другим (слова, разговор).

Информационные модели делятся на образно-знаковые и знаковые модели.

Фотографии, географические карты, диаграммы – это образно-знаковые модели, они учитывают цвет и форму. Их можно разделить на:

1) геометрические (чертеж, план, карта, рисунок) отображающие внешний вид оригинала;

2) структурные модели отображающие строение объектов и связи их параметров (таблица, граф, схема, диаграмма);

3) словесные модели зафиксированные средствами языка;

4) алгоритмическая модель(нумерованный список, блок-схема).

Знаковые модели делятся на:

1) математические модели представленные математическими формулами, отображающие связи различных параметров объекта, системы, процесса;

2) специальные модели представленные на специальных языках (химические формулы, ноты и др.);

3) алгоритмические модели представлены в виде программы записанной на специальном языке программирования.

Имитационное моделирование – это процесс конструирования на ЭВМ сложной реальной системы функционирующей во времени и подстановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии обеспечив функционирование данной системы.

Модель детерминированная

Если каждому входному набору параметров соответствует вполне определенный и однозначно определенный набор выходных параметров. В противном случае модель не детерминированная (стохастическая, вероятностная).

Пример: Рассматривается физическая модель свободного падения тела.

Данная модель является детерминированной.

Если бы учли случайный параметр, например порыв ветра с силой p при падении тела, то S считалось бы по другой формуле: S = (g(p) · t²)/2 и модель называлась бы стохастической.

Модель логическая

Если она представима предикатами или логическими функциями.

Пример: Совокупность двух логических функций

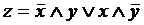
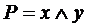
может служить математической моделью одноразрядного сумматора.

Модель игровая

Если она описывает, реализует некоторую игровую ситуацию.

Модель алгоритмическая

Если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим её функции.

Пример: Алгоритмической моделью квадратного корня может служить алгоритм вычисления его приближенного сколь угодно точного отношения по известной рекуррентной формуле.

Модель визуальная

Если она позволяет визуализировать отношения и связи моделируемой системы.

Модель натурная

Если она материальная копия объекта моделирования.

Пример: Глобус.

Модель геометрическая

Если она представима геометрическими образами и объектами.

Пример: Прямая линия является моделью числовой оси.

Параллелограмм является моделью плоскости, либо моделью квадрата.

Модель клеточно-автоматная

Если она представляет систему с помощью клеточного автомата.

Пример: Классическая клеточно-автоматная модель: игра «жизнь» Дж. Конвея.

Модель фронтальная

Самая сложная, она описывает эволюцию моделируемой систему эволюции фронтальных объектов.

Пример: Множество Кантора.

Возьмем отрезок [0; 1] и разобьем его на три части.

Выбросим из донного отрезка средний отрезок и каждый из оставшихся отрезков опять разобьем на три части.

Из каждого отрезка выбросим средние части и каждый из оставшихся отрезков опять разобьем на три части.

Продолжая разбиение таким образом получим множество называемое множеством Квантора.

В пределе получаем несчетное множество изолируемых точек.

Фронтальная модель применяется обычно тогда, когда реальный объект нельзя представить в виде классической модели. Когда имеем дело с нелинейностью (много вариантностью) путей развития, необходимостью выбора и недетерминированностью (хаотичностью и необратимостью) процесса.

Пример: Математические модели динамики эпидемии инфекционной болезни, радиоактивного распада, усвоение второго иностранного языка и др..

Компьютерное моделирование

Компьютерное моделирование – основа представления знаний в ЭВМ.

Компьютерное моделирование для рождения новой информации использует любую информацию, которую можно актуализировать с помощью ЭВМ.

Процесс моделирования связан с разработкой систем компьютерного моделирования.

Разновидностью компьютерного моделирования является вычислительный эксперимент, т. е. эксперимент осуществляемый с помощью компьютерной среды или технологии.

Вычислительный эксперимент становится новым инструментом, методом научного познания новой технологии из-за необходимости исследования сложных и нелинейных математических моделей системы.

Вычислительный эксперимент позволяет находить новые закономерности, проверять гипотезы, визуализировать ход событий.

Пример: Модель повторяющейся эпидемии.

Решение краевых задач.

Опр. Краевой задачей называется задача, в которой определённым образом задано условие на краях исследуемой области. Условия определяют поведение искомой функции.

Опр. ( постановка краевых задач).

Решить дифференциальное уравнение y"=f(x,y,y'), при чём обязательно заданы граничные условия. Найти значения y в каждой точке фиксированной x.

Краевые задачи делятся на разные виды в зависимости от начальных условий:

1. Если граничные условия имеют вид: y(a)=A, y(b)=B. Где А и В либо константы, либо функция, то это краевые условия первого рода.

2. Если граничные условия имеют вид: y'(a)=A, y'(b)=B, то это краевая задача второго рода.

3. Если известны комбинации: α₁·y'(a)+β₁·y(a)=γ₁ и

α₂·y'(a)+β₂·y(a)=γ₂ то это краевая задача третьего рода.

Для задач первого рода известна функция, т.е. например, известно значение температуры на краях стержня.

Для задач второго рода на границах сама функция неизвестна, а известна её производная.

Для задач третьего рода неизвестно значение функции, неизвестна производная, а известна их комбинация.

Краевые задачи делятся на три основных типа:

1. Параболического типа (пример: уравнения теплопроводности).

2. Гиперболического типа (уравнение описывающее колебание струны).

3. Эллиптического типа.

Рассмотрим краевую задачу 2-го рода параболического типа.

Задача: (моделирует процессы теплопереноса).

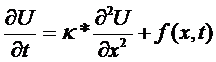
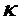- коэффициент.

f – функция внутренних тепловых источников.

U – температура.

Начальные условия:

U(x,0)=φ(x)

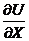_x=a = f(t) - левое граничное условие

U(b)=q(t) - правое граничное условие

Для её решения использую метод сеток.

Решение:

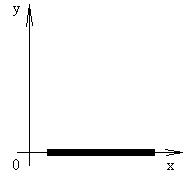Изобразим декартовую систему координат, где отложим х (точка стержня) и у (момент времени).

Рассмотрим стержень.

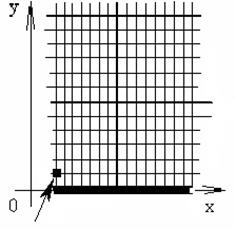
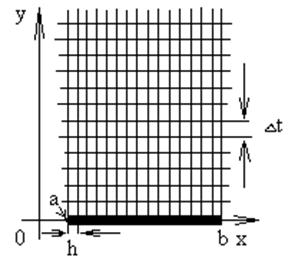Разобьем участок стержня на n равных частей и рассмотрим шаг h=(b-a)/n (см. рисунок).

Для выбора шага по времени используем условие устойчивости: 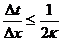это условие применяется для явной сетки, когда последующий слой считается через предыдущий. Если это условие будет не соблюдаться, то в программе могут возникать неадекватные результаты: очень большие числа или числа разных знаков. Обычно 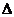t приходится выбирать очень маленьким, например 0,001, 0,0001, что затрудняет процесс счёта на компьютере. Например реальный процесс, который происходит 2 секунды моделируется на компьютере 2 часа.

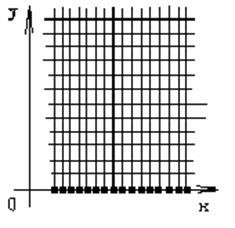Используя условие U(x,0)=φ(x) мы можем найти значение температуры в каждой точке стержня в начальный момент времени, т.е. посчитать значение в следующих узлах сетки:

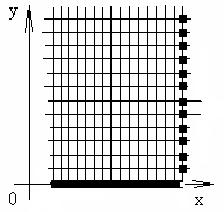Используя, правое граничное условие, мы найдём значение температуры на правом краю стержня во все моменты времени. На сетке эти точки будут расположены следующим образом:

(см. рисунок).

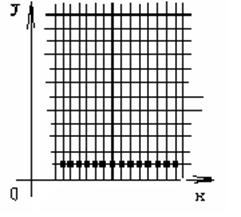
Затем, используя основное уравнение теплопроводности и выразив последующий слой через предыдущий мы можем найти значения температуры в следующих точках (см. рисунок).

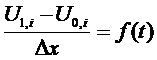И наконец распишем производную на левой границе: Найдём значение в точке U_0,I:

U_0,i= U_1,i-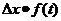

Значение в данной точке будет соответствовать следующему узлу сетки (см рисунок).

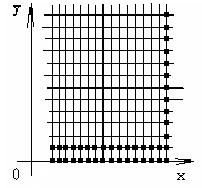Таким образом мы посчитаем значения температуры в следующих узлах (см. рисунок)

Таким образом мы можем посчитать температуру во всей сетке (во всех узлах) и будем знать температуру стержня в каждой точке стержня в каждый момент времени.(Для получения более подробных сведений обращаётесь в раздел численных методов – решение краевых задач.)

Алгоритм программы.

В программе можно использовать два одномерных массива, либо один двумерный массив.

Одномерный массив описывается следующим образом:

U0[0..n] – используется для хранения данных предыдущего слоя,

U1[0..n] – используется для хранения данных последующего слоя.

Задаём начальные условия в цикле, т.е. для каждой точки стержня задаём значение температуры в нулевой момент времени:

For i:=0 to nx do { n - количество разбиений стержня}

Begin

U0[i]=φ(x) {в качестве φ(x) ,берётся функция из граничного условия}

x:=i*dx {dx –шаг, который задаётся в начале программы самостоятельно}

Затем открываем цикл по времени:

For j:=1 to T do {T – конечный момент времени}

Begin

U1[n]:=q(t1) { в качестве q(t1) ,берётся функция из правого граничного условия }

t1:=dt*j { dt –шаг, который задаётся в начале программы исходя из условия устойчивости – тоже самое что и }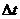

Затем решаем основное уравнение теплопроводности. Предварительно расписав его в разностном виде:

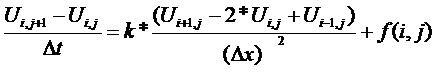
Где U_i,j+1 - это U[i]

U_i,j - это U0[i]

U_i+1,j - это U0[i+1]

U_i-1,j - это U0[i-1]

Выражаем последующий слой через предыдущий:

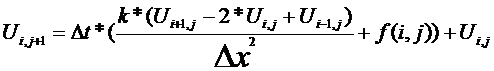
т.е. for i:=1 to n-1 do

U1[i]:=dt*(k*(U0[i+1]-2*U0[i]+U0[i-1])/(dx*dx)+f(i))+U0[i]

Т.о. мы посчитаем температуру на следующем слое , в точках соответствующих индексам от 1 до n-1.

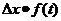Используя левое граничное условие найдём: U_0,i= U_1,i- т.е.

U1[0]:=U1[1]-dx*f(t) {где f(t) функция т левого граничного условия}

Затем выводим слой (результат) на экран:

For i:=0 to 1 do

Write(u1[i]);

Writeln;

Переприсваиваем слои:

U0:=U1 ;

Заканчиваем цикл по времени. Заканчиваем программу.

Колебание струны

С помощью дифференциальных уравнений описываются погодные процессы (перенос теплого и холодного воздуха), конвективные процессы (процессы обмена слоями воздуха или газа в жидкости). Наличие турбулентности (присутствие вихря) приводит к тому, что трудно рассчитать в какой точке какая будет температура. Кроме уже выделенных уравнений для описания конвективных процессов добавляются ещё дополнительные уравнения, т.е. модель усложняется.

Системой дифференциальных уравнений описывают тепловые процессы в таких областях как авиа и ракетостроение. Например топливный бак подвергается значительному механическому и тепловому воздействию.

Классическая задача колебания струны состоит в следующем: струна с концами А,В закреплена в точках А и В, либо подвергается механическому воздействию в этих точках, при этом точка А или точка В начинает отклонятся от положения равновесия. Это отклонение можно обозначить какой-нибудь функцией, например функцией U. Тогда классической задачей о поведении струны при механическом воздействии называется следующая задача: решается уравнение второго порядка

которое описывает отклонение от положения равновесия точек внутри струны.

Начальные условия: (условие начального слоя)

Краевые условия: - левое граничное условие

- правое граничное условие.

Решить эту задачу, значит найти отклонение положения струны от равновесия, т.е. найти U в каждый момент времени.

Алгоритм

Задаём массивы (3 массива) –для хранения данных каждого из 3-х слоёв.

U1 – задаёт условия начального слоя;

U2 – определяется функцией на следующем слое (втором);

U3 – определяется значение на следующем слое (третьем).

1. U1 –задано функцией

2. _t=0 = g(x) ; это отсюда нам необходимо выразить U2[x] (самостоятельно)

Благодаря этому условию, мы можем посчитать значения второго слоя.

4. Открываем цикл по времени

for k;2 to n do

begin

3. Распишем основное уравнение

Выразив U3[x], мы можем в цикле (for x:=0 to n-1 do) посчитать все значения отклонения для каждой точки х на третьем слое, за исключением правой граничной точки на этом же слое.

4.Для нахождения значения в правой граничной точке мы используем правой граничное условие, например , т.е. мы знаем значения в крайней правой точке стержня равной b для любого момента времени. (возможно будет дана не функция а её производная, тогда необходимо её расписать и выразить U3 в точке b ).

Затем вывод U3 и переприсваивание массивов:U1:=U2, U2:=U3;

Закрываем цикл по времени.

Программа на Pascal аналогична первой (для уравнения теплопроводности), составить самостоятельно.

Пример использования системы дифференциальных уравнений в биологии.

Примером использования системы дифференциальных уравнений в биологии является модель биоценоза с учётом введённых допущений.

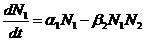
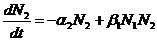
N₁ –число жертв.

N₂ –число хищников.

α₁ – коэффициент естественного прироста жертв.

α₂ – коэффициент естественной убыли хищников.

β₁ – коэффициент уничтожения хищниками своих жертв.

β₂ – коэффициент защиты жертв от хищников.

Уравнение приводится к нормированному виду – это освобождение от всяких масштабных единиц, тогда система имеет вид:

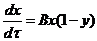
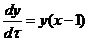
где 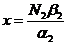относительное число жертв.

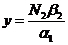относительное число хищников.

τ- нормированное время.

B= 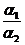- коэффициент.

Данная система решается в среде MathCad, здесь же строятся графики зависимости х от τ и у от τ.

Графы.

Рассмотрим основное средство создания информационных моделей. К ним можно отнести словесное описание объекта (художественное вещества, статья о нём в словаре). Самым распространённым методом в создании информационной модели является метод описания.. Другим распространённым методом построения и визуализации информационных моделей является графы.

Граф-это отражение некоторого отношения установленного между фиксированными множествами. Из двух множеств в составляющих графа -одно это множество элементов (вершины) а другое множество связей между ними (линии произвольной конфигурации). Граф состоит из множества вершин x и связей между ними U, обозначается G(x,U).

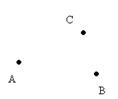
Пример. Известно, что трое учеников учащихся в одном классе помогают друг другу по разным предметам. Изобразим граф отражающий отношение помощи учащихся:

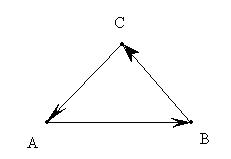
Если порядок соединения не важен, а важно то как они соединены, то такое соединение называют ребром графа А-В. Если важен порядок соединения вершин то такое соединение называют дугой графа и обозначают →.

Граф у которого вершины соединены дугами называют ориентированным. Граф у которого вершины соединены рёбрами называют неориентированным. Граф, вершины которого соединены и дугами и рёбрами называют смешанным.

Две вершины графа называют смежными, если они определяют дугу или ребро. Если вершина являются началом или концом дуги, то говорят, что вершина инцидентна дуге или ребру. Вершины не инцидентные никакому ребру или дуге называют изолированными.

Вершина инцидентная только одному ребру или дуге называется висячей.

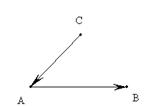
Ребро или дуга, граничными вершинами которой является одна и та же вершина называется петлёй.

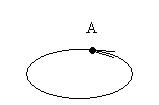
Виды графов.

Граф без петель и кратных рёбер (дуг) называется обыкновенным (простым, скелетным, графом Берже).

Граф без петель, но с кратными рёбрами (дугами называют мультиграфом).

Граф, соединённый только изолированными вершинами называется пустым или ноль графом.

Обыкновенный граф, в котором любые две вершины соединены ребром называются сльносвязанным или полным графом.

Части графов.

Подграфом С графа G называют граф, образованный из графа G опусканием некоторых вершин и инцидентных им рёбер. Исходный граф по отношению к подграфу является надграфом.

2. подграф графа 1

1. надграф графа 2

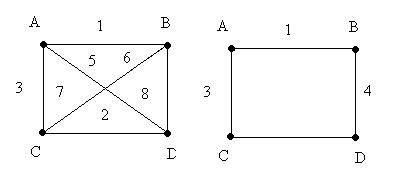
1) 2)

Если в результате преобразований число вершин осталось прежним, но были опущены некоторые ребра (дуги)/, то вновь образованный граф считают частичным графом (субграфом) исходного графа.

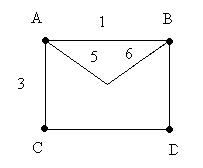Данный граф является субграфом графа 1, а исходный граф 1 является сверхграфом.

3)

Маршруты

Маршрут определяется как некоторая последовательность ребер, в котором граничные вершины двух соседних ребер совпадают, например, последовательность ребер 1, 4, 8, 6 – маршрут.

Маршрут, все ребра которого разложены, называется цепью, например, 5, 6, 4, 2.

Замкнутая цепь – это цепь возвращающаяся в ту же вершину, из которой начиналась и она называется циклом, например, 5, 7, 3.

Граф, любая пара вершин которого может быть соединена маршрутом, называется связным, например, 1-3 – связные.

Несвязный граф представляет собой совокупность отдельных частей (подграфов) называемых компонентами связности, например:

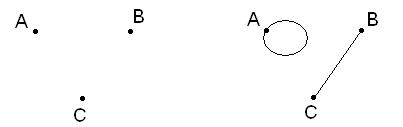
4) 5)

Связный граф не создающий циклов, называется деревом, например:

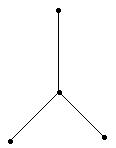
Дерево имеет n вершин, соединенных n-1 ребром.

Несвязный граф, компоненты которого являются деревьями, называется лесом, например:

Способы задания графа

Произвольный граф можно задать совокупностью двух множеств – множество вершин и множество ребер. Вторым способом задания графа является представление его с помощью матрицы.

Матрица связности имеет вид квадратной таблицы, в которой представлены отношения между вершинами, где элемент матрицы – это количество связей (ребер или дуг) для других двух вершин. Если вершины смежные, то ячейка таблицы примет значение 1, если вершины соединены краевыми ребрами, то ячейка таблицы примет значение 2. Так для графа, представленного на рис.1 матрица связности будет иметь вид таблицы.

	A	B	C	D	E
A
B
C
D
E

Из таблицы видно, что наибольшая лок. степень у вершины E: P(E)=4, у всех остальных вершин лок. степень равна 3.

Для того чтобы включенную в структуру модель представить в виде графа не структурную (количественную или текстовую) информацию довольно часто любому ребру (или любой вершине) рассматриваемого графа приписывают некоторый вес.

Граф, ребра (вершина) которого приписаны весу, называется взвешенными. Вес неудобно располагать на чертеже и схеме, поэтому взвешенный граф лучше представить в виде матрицы, такие матрицы называются матрицами весовых соотношений.

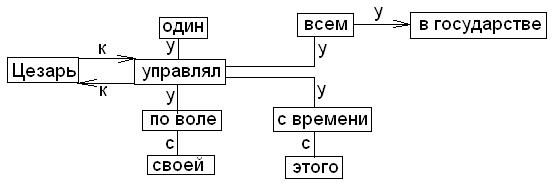
Пример: Составить взвешенный граф предложения: “С этого времени Цезарь один управлял всем в государстве по своей воле”.

В этом графе вершинами будут члены предложения, дуги синтетической связи между ними, причем вес приписан и вершинам и дугам, чтобы указать направление дуги в матрице используется знак “+” и “-“ (“+” - главное слово, “-“ -зависимое) связи, которую нужно отразить.

у – управление

с – согласные

к – координация

ПРАКТИЧЕСКАЯ ЧАСТЬ.

Моделирование физической и биологической задачи.

Задача о пушке, которой надо попасть в крепость.

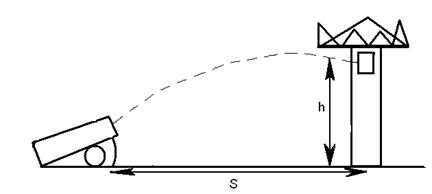
Известна высота башни h и расстояние S до неё. Найти угол 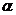, при котором снаряд из пушки попадёт в башню на высоте h.

Решение.

(см в лекциях)

Горизонтальное и вертикальное смещение снаряда за время t описывается формулами:

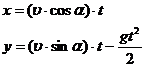
где 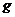- ускорение свободного падения = 9.8 и 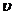- начальная скорость вылета снаряда.

Выразим t из первой формулы и подставим во вторую:

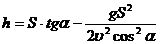
Задача сводится к решению методом половинного деления где 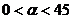. Метод половинного деления или аналог в артиллерийском приёме (пристреле) – одно положение выше цели, второй выстрел ниже цели.

Алгоритм метода половинного деления смотри в численных методах.

Текст программы на Pascal:

program n1;

uses crt;

var v,h,s:integer;

a1,a2,a,h1,h2,hh:real;

begin

clrscr;

writeln('Введите начальную скорость');

readln (v); { Ввод с клавиатуры скорости }

writeln('Введите расстояние до цели');

readln(s); { Ввод с клавиатуры расстояния }

writeln('Введите высоту цели');

readln(h); { Ввод с клавиатуры высоты }

a1:=0; {начальный угол}

a2:=89; {конечный угол}

a:=(a1+a2)/2; {искомый угол т.е промежуточный угол}

hh:=s*(sin(pi/180*a)/cos(pi/180*a))-(9.8*s*s)/(2*v*v*cos(pi/180*a)*cos(pi/180*a));

{высота полёта при искомом угле}

while abs(hh-h)>0.01 do

{пока разность между искомым и полученным углом больше 0.001 то выполнять цикл}

begin

if hh>h then a2:=a ;

{если полученная высота больше искомой, то а2 = промежуточному углу}

if hh<h then a1:=a;

{если полученная высота меньше искомой, то а1 = промежуточному углу}

a:=(a1+a2)/2; (искомый т.е. промежуточный угол = середине между а1 и а2)

hh:=s*(sin(pi/180*a)/cos(pi/180*a))-(9.8*s*s)/(2*v*v*cos(pi/180*a)*cos(pi/180*a));

{расчёт новой высоты при новом промежуточном угле}

end;

write('Угол =',a); {вывод полученного угла}

readkey;

end.

Например, угол, при котором пушка попадёт на высоту 5, на расстоянии 10 при начальной скорости 20 равен 34 градуса.

Задания:

Найти необходимый угол выстрела, при скорости вылета снаряда 20, на расстояние 5, чтобы снаряд попал в цель на высоте 5.

Найти необходимый угол выстрела, при скорости вылета снаряда 15, на расстояние 5, чтобы снаряд попал в цель на высоте 5.

Найти необходимый угол выстрела, при скорости вылета снаряда 20, на расстояние 10, чтобы снаряд попал в цель на высоте 15.

Сделайте вывод о зависимости между необходимым углом и скоростью вылета снаряда;

Сделайте вывод о зависимости между необходимым углом и расстоянием до цели;

Сделайте вывод о зависимости между необходимым углом и высотой цели;

Сделайте вывод о зависимости между всеми параметрами модели.

Задача о кроликах и лисах.

На некотором острове живут лисы и кролики. Кролики питаются травой, а лисы кроликами. Экологи пересчитывают кроликов и лис и сделали вывод:

1. Коэффициент прироста числа кроликов зависит от колебания погоды (холодная или тёплая) и колеблется от 3.2 до 4.7

2. Коэффициент прироста числа лис при избытке крольчатины колеблется от 5.2 до 5.7. При недостатке прирост пропорционален приросту кроликов.

3. Коэффициент пропорциональности =50

Требуется установить, как меняется численность кроликов, и лис с течением времени.

Построение модели и схему взаимодействия лис и кроликов смотри в лекциях.

Текст задачи на Pascal:

program n2;

uses crt;

var i,n:integer;

m,m1,l1,l,

k,a:real;

begin

clrscr;

write('vvedite kolichestvo let');

readln(n);

write('vvedite nachalnoe kolichestvo krolikov');

readln(m);

write('vvedite nachalnoe kolichestvo lis');

readln(l);

write('vvedite koefficient prirista krolikov');

readln(k);

write('vvedite koefficient prirista lis');

readln(a);

for i:=1 to n do

begin

m1:=(1+k)*m-50*l;

if a<(m1-m)/50 then l1:=(1+a)*l else l1:=(1+(m1-m)/50)*l;

l:=l1;

m:=m1;

end;

writeln('kolichestvo lis = ',l);

writeln('kolichestvo krol = ',m);

readkey;

end.

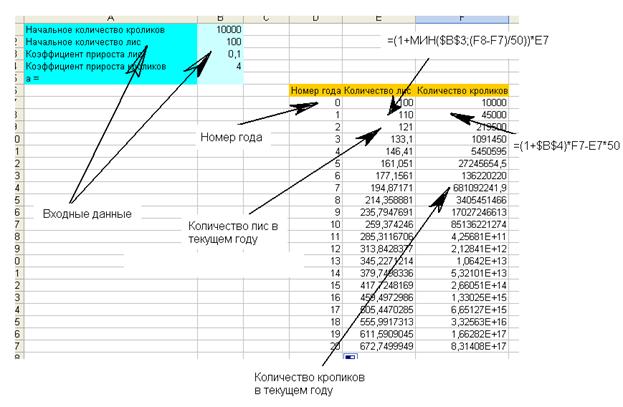
Решение в Excel:

На рисунке видно, что в ячейки B1-B4 вводим исходные данные. В ячейку E8 вводим формулу =(1+МИН($B$3;(F8-F7)/50))*E7 затем растягиваем ячейки вниз на необходимое количество лет (в данном примере 21 год; от 0 до 20). В ячейку =(1+$B$4)*F7-E7*50 и аналогично растягиваем. В результате в ячейках E7-E27 получим количество лис в соответствующих справа годах. В F7-F27 – количество кроликов. Например, видно, что при начальном количестве кроликов = 10000, при количестве лис = 100, и коэффициентах роста для кроликов = 4 и лис =0,1 количество кроликов через 10 лет будет 85136221274 а лис 259.

Задания:

Исследуйте по модели количество кроликов и лис при начальном количестве 1000 кроликов. Что произошло? В чём погрешность модели?

Исследуйте по модели количество кроликов и лис при начальном количестве 10000 кроликов и различных коэффициентах роста кроликов и лис. Сделайте выводы.

Сделайте выводы о взаимосвязи между различными параметрами.

Краевые задачи:

Используя метод конечных разностей решить краевую задачу:

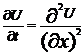
U(x,0)=2*cos(x+0.55)

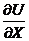_x=a = sin(t)

U(0.6,t)=0.817+2*t

Текст задачи на Pascal

Program kraevaya_zadacha;

uses crt;

const x0 = 0; {начальная точка стержня}

dx = 0.1; {шаг разбиения стержня}

nx = trunc(0.6/dx); {количество разбиений }

t0 = 0; {начальный момент времени}

dt = 0.001; {шаг по времени –берётся из условия устойчивости }

T = 20; {количество промежутков времени}

var u0,u1:array [0..nx] of real;

x,t1:real;

i,j,i1:integer;

begin

clrscr;

{ ========================Вывод на экран строки значений х ================}

write (' ':7);

for i:=0 to nx do

begin

x:=x0+i*dx;

write('|',x:7:4);

end;

writeln;

writeln('---------------------------------------------------------------');

{========Вычисление в цикле значения температуры в начальный момент времени===}

for i:=0 to nx do

begin

x:=x0+i*dx;

u0[i]:=2*cos(x+0.55);

end;

for j:=0 to T do {открываем цикл по времени}

begin

t1:=t0+j*dt;

u1[nx]:= 0.817+2*t1; {Задаём правое граничное условие}

for i:=1 to nx-1 do

{=================Вычисление температуры на следующем слое}

U1[i]:=(dt*(U0[i+1]-2*U0[i]+U0[i-1]))/(dx*dx)+U0[i] ;

U1[0]:= U1[1]-dx*sin(t1); {вычисление левого граничного условия}

{=======================Вывод результатов на экран}

write(t1:7:4);

for i1:=0 to nx do

write ('|',u1[i1]:7:4);

writeln;

U0:=U1; {переприсваивание массивов}

End; {Закрытие цикла по времени}

end.

Решение в Excel:

На рисунке видно, что в ячейках C23-I23 содержаться точки стержня (от 0 до 0.6). В ячейках B2-B22 содержаться значения моментов времени. Тогда на пересечении строки и столбца находится соответствующие искомые значения.

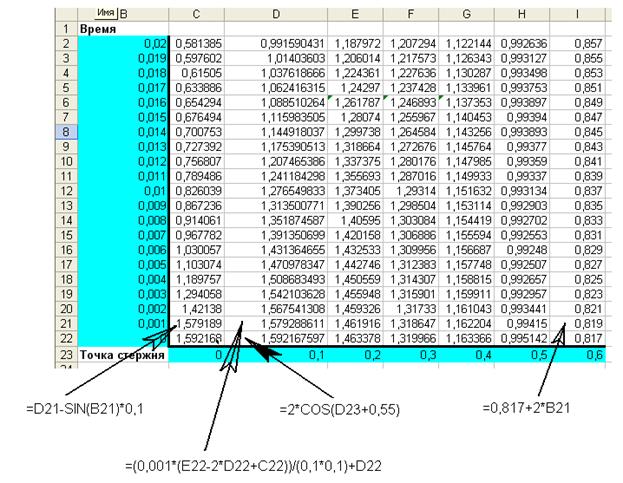
В ячейку С22 вводим формулу =D22-SIN(B22)*0,1 затем растягиваем её вверх до С2 (из условия 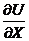_x=a = sin(t)). В ячейку D22 вводим =2*COS(D23+0,55) и растягиваем до ячейки H22 (из условия U(x,0)=2*cos(x+0.55)). Вводим в I22 формулу =0,817+2*B22 (из условия U(0.6,t)=0.817+2*t) и растягиваем вверх до I2. Затем в D21 вводим формулу =(0,001*(E22-2*D22+C22))/(0,1*0,1)+D22 (из условия 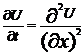) и растягиваем от D21 вверх и вправо до H2. В результате мы получим значения для каждой точки в каждый момент времени.

Задания: сравните данные таблицы с результатами работы программы на Pascale.

Моделирование в среде MathCAD задачи «Хищники и жертвы».

Составим по данной математической модели программу на языке MathCAD (см. теорию), и определим колебания числа жертв и хищников, решив нелинейные дифференциальные уравнения:

Выбираем стандартную функцию ORIGIN

ORIGIN:=1

B:=4 {из данных}

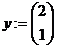{столбец неизвестных}

F(t,y):=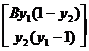

ORIGIN:=0

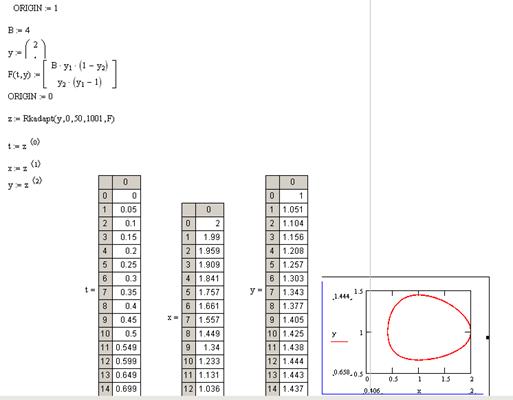
z:=Rkadapt(y,0,50,1001,F)

t:=z⁽⁰⁾

x:=z⁽¹⁾

y:=z⁽²⁾

Строится график:

Доц.Богданова М.В.

Уважаемые студенты!

Вашему вниманию предлагается курс лекций и

содержание практических занятий, после изучения