Анализ качества эмпирического уравнения множественной линейной регрессии

Проверка статистического качества оцененного уравнения регрессии проводится по следующим направлениям:

• проверка статистической значимости коэффициентов уравнения регрессии;

• проверка общего качества уравнения регрессии;

• проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).

Статистическая значимость коэффициентов множественной линейной регрессии с т объясняющими переменными проверяется на основе t-статистики:

.

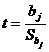(6.31)

имеющей в данной ситуации распределение Стьюдента с числом степеней свободы 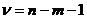(п — объем выборки). При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точкой 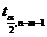распределения Стьюдента.

Если 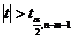коэффициент 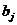считается статистически значимым. В противном случае коэффициент 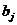считается статистически незначимым (статистически близким к нулю), то есть фактор 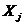линейно не связан с зависимой переменной Y и его можно исключить из набора объясняющих переменных.

Зачастую строгая проверка значимости коэффициентов заменяется простым сравнительным анализом.

Если 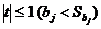, то коэффициент статистически незначим.

Если 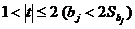, то коэффициент относительно значим. В данном случае рекомендуется воспользоваться таблицей критических точек распределения Стьюдента.

Если 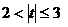, то коэффициент значим. Это утверждение является гарантированным при 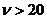и .

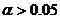Если 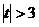, то коэффициент считается сильно значимым.

Вероятность ошибки в данном случае при достаточном числе наблюдений не превосходит 0,001.

После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии. Для этой цели, как и в случае парной регрессии, используется коэффициент детерминации 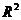, который в общем случае рассчитывается по формуле

.

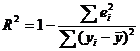(6.32)

Для линейного уравнения регрессии данный показатель может быть рассчитан через 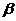- коэффициенты:

.

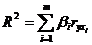(6.33)

Для множественной, регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение 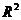. Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы. Вводится так называемый скорректированный (исправленный) коэффициент детерминации:

.

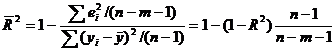(6.34)

Здесь 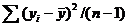является несмещенной оценкой общей дисперсии — дисперсии отклонений значений переменной Y от 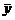. При этом число ее степеней свободы равно 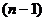. Одна степень свободы теряется при вычислении .

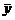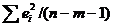является несмещенной оценкой остаточной дисперсии — дисперсии случайных отклонений (отклонений точек наблюдений от линии регрессии). Ее число степеней свободы равно 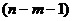. Потеря 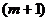степени свободы связана с необходимостью решения системы 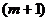линейного уравнения при определении коэффициентов эмпирического уравнения регрессии. Несмещенная оценка объясненной дисперсии (дисперсии отклонений точек на линии регрессии от 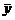) имеет число степеней свободы, равное разности степеней свободы общей дисперсии и остаточной дисперсии .

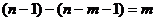Коэффициент детерминации в настоящее время рассматривается лишь как один из ряда показателей, который нужно проанализировать, чтобы уточнить строящуюся модель.

Анализ статистической значимости коэффициента детерминации

После оценки индивидуальной статистической значимости каждого из коэффициентов регрессии обычно анализируется совокупная значимость коэффициентов, то есть гипотеза об общей значимости — гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

.

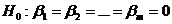Проверка данной гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсий.

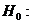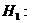(объясненная дисперсия)=(остаточная дисперсия),

(объясненная дисперсия)>(остаточная дисперсия).

Строится F-статистика:

,

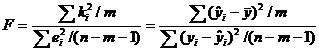(6.35)

где 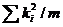- объясненная дисперсия, 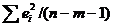- остаточная дисперсия. При выполнении предпосылок МНК построенная F-статистика имеет распределение Фишера с числами степеней свободы 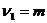, 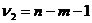. Если при требуемом уровне значимости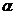 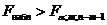(где 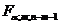- критическая точка распределения Фишера), то 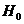отклоняется в пользу 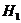, то есть объясненная дисперсия существенно больше остаточной дисперсии, а значит уравнение регрессии качественно отражает динамику изменения зависимой переменной Y.

Если 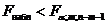, то нет оснований для отклонения 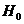, то есть объясненная дисперсия соизмерима с дисперсией, вызванной случайными факторами, и совокупное влияние объясняющих переменных модели несущественно, а следовательно, общее качество модели невысоко.

На практике вместо указанной гипотезы проверяют гипотезу о статистической значимости коэффициента детерминации :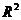

,

.

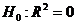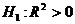Для проверки данной гипотезы используется следующая F-статистика:

.

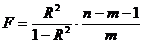(6.36)

Очевидно, что показатели F и 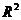равны или не равны нулю одновременно. Нулевая гипотеза отклоняется, если 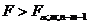. Это равносильно тому, что 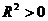, т.е. 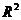статистически значим.

Однако статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации 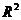не гарантирует высокое качество уравнения регрессии.

Статистика Дарбина—Уотсона

Наиболее известным критерием обнаружения автокорреляции между соседними членами является критерий Дарбина-Уотсона. Он основан на простой идее: если корреляция ошибок регрессии не равна нулю, то она присутствует и в остатках регрессии 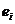получающихся в результате применения обычного метода наименьших квадратов.

Для анализа коррелированности отклонений вместо коэффициента корреляции

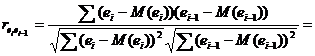	(6.37)
,

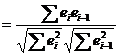используют тесно с ним связанную статистику Дарбина-Уотсона DW, рассчитываемую по формуле

.

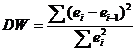(6.38)

Действительно,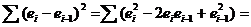

.

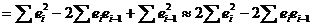Здесь сделано допущение, что для больших 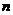справедливо соотношение: .

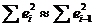Тогда

.

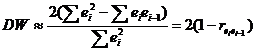(6.39)

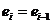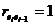Если , то (положительная автокорреляция) и 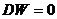. Если 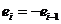, то 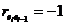(отрицательная автокорреляция) и 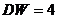. Если 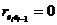(автокорреляция отсутствует), то 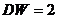. Во всех других случаях .

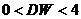Необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина—Уотсона. Тогда, если 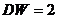, мы считаем отклонения от регрессии случайными.

Это означает, что:

· построенная линейная регрессия, вероятно, отражает реальную зависимость;

· скорее всего, не осталось неучтенных существенных факторов, влияющих на зависимую переменную;

· какая-либо другая нелинейная формула не превосходит по статистическим характеристикам предложенную линейную.

Возникает вопрос, какие значения DW можно считать статистически близкими к двум? Для ответа на этот вопрос разработаны специальные таблицы критических точек статистики Дарбина—Уотсона, позволяющие при данном числе наблюдений 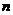, количестве объясняющих переменных 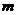и заданном уровне значимости 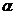определять границы приемлемости (критические точки) наблюдаемой статистики DW.

Для заданных 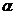, , 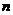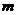в таблице указываются два числа: 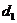- нижняя граница и 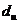-верхняя граница. Для проверки гипотезы об отсутствии автокорреляции остатков используется числовой отрезок, изображенный на рис. 6.3.

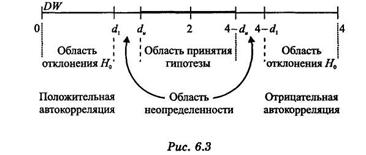
Выводы осуществляются по следующей схеме.

Если 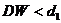, то это свидетельствует о положительной автокорреляции остатков.

Если 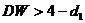, то это свидетельствует об отрицательной автокорреляции остатков.

При 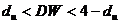гипотеза об отсутствии автокорреляции остатков принимается.

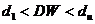Если или 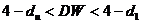, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.

Не обращаясь к таблице критических точек Дарбина—Уотсона, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если .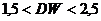

При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным.