Расчет коэффициентов множественной линейной регрессии
Представим данные наблюдений и соответствующие коэффициенты в матричной форме.
, 
, 
, 
.
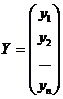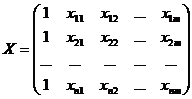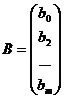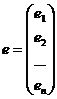Здесь Y -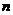 
-мерный вектор-столбец наблюдений зависимой переменной Y; X - матрица размерности 
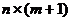, в которой 
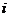-я строка ( 
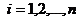) представляет наблюдение вектора значений независимых переменных 
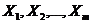;единица соответствует переменной при свободном члене 
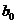; В — вектор-столбец размерности (m+1) параметров уравнения регрессии; е — вектор-столбец размерности n отклонений выборочных (реальных) значений 
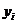зависимой переменной Y от значений 
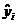, получаемых по уравнению регрессии
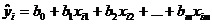 . | (6.12) |
Нетрудно заметить, что функция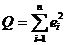 
в матричной форме представима как произведение вектор - строки 
на вектор - столбец 
. Вектор-столбец 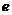в свою очередь может быть записан в следующем виде:
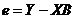 . | (6.13) |
Тогда
.
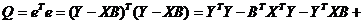
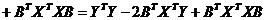Здесь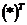 
обозначение транспонированной матрицы.
При выводе последней формулы использовались известные соотношения линейной алгебры:
.
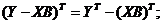
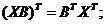
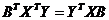Эти соотношения легко проверить, записав поэлементно все матрицы и выполнив с ними нужные действия.
Необходимым условием экстремума функции Q является равенство нулю ее частных производных по всем параметрам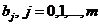 
, т.е.
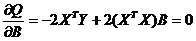 . | (6.14) |
Отсюда, получаем систему нормальных уравнений в матричной форме для определения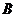 
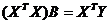 . | (6.15) |
Решением уравнения (6.15) является
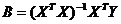 . | (6.16) |
Матрица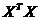 
представляет матрицу сумм первых степеней, квадратов и попарных произведений 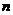наблюдений объясняющих переменных:
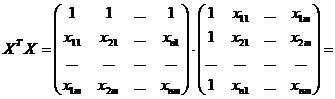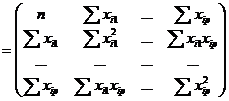  . | (6.17) |
Матрица
 . | (6.18) |
В частном случае из рассматриваемого матричного уравнения (6.15) с учетом (6.17) и (6.18) для одной объясняющей переменной (m=1) можно получить уже рассмотренную ранее систему нормальных уравнений в матричном виде:
.
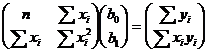Кроме того, для линейной множественной регрессии существует другой способ оценки параметров – через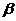 
- коэффициенты (параметры уравнения в стандартизованном масштабе).
При построении уравнения в стандартизованном масштабе все значения переменных переводятся в стандартизованные значения по формулам:
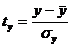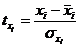 ,.  . | (6.19) |
Таким образом, начало отсчета каждой стандартизованной переменной совпадает с ее средним значением, а в качестве единицы измерения принимается ее среднее квадратическое отклонение. Стандартизованные переменные будут связаны линейным соотношением:
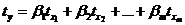 , | (6.20) |
здесь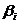 
- стандартизованные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии ( 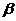- коэффициенты) определяются из следующей системы уравнений:
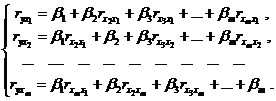 | (6.21) |
Найденные из данной системы 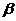- коэффициенты позволяют определить значения коэффициентов регрессии 
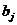в естественном масштабе по формулам:
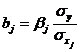 . | (6.22) |
Параметр 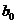определяется из условия
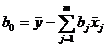 . | (6.22*) |
На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии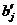 
и коэффициенты эластичности 
( 
):
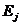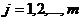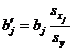 , | (6.23) |
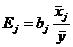 . | (6.24) |
Стандартизованный коэффициент регрессии 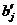показывает, на сколько величин оценки своего среднего квадратического отклонения 
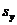изменится в среднем зависимая переменная Y при увеличении только 
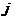-й объясняющей переменной на величину оценки своего среднего квадратического отклонения 
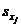при неизменном влиянии прочих факторов модели.
Коэффициент эластичности 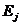показывает на сколько процентов (от средней) изменится в среднем Y при увеличении только 
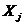на 1% от своего среднего уровня при фиксированном положении других факторов модели.
Частные коэффициенты эластичности и стандартизованные частные коэффициенты регрессии можно использовать для ранжирования факторов по силе влияния на результат. Чем больше величина коэффициента, тем сильнее влияет фактор результат.
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта - коэффициентов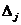 
:
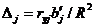 , | (6.25) |
где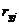 
- коэффициент парной корреляции между фактором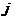 
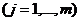и зависимой переменной.