Частные производные высших порядков

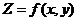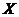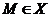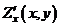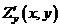Пусть определена на множестве и в каждой точке существуют (первые) частные производные и . Первые частные производные представляют собой новые функции двух переменных. Частные производные от функци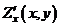й и 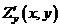называются частными производными второго порядка (или вторыми частными производными) от функции .

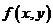Таким образом, имеем четыре вторых частных производных, которые обозначаются:

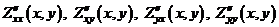
или

.

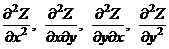Частные производные второго порядка 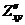и 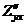называются смешанными частными производными. Если смешанные частные производные непрерывны, то они обязательно равны.

Пример 22. Найти все частные производные второго порядка от функции .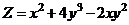

Решение

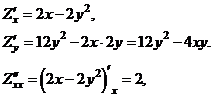
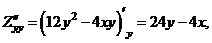
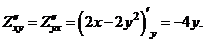
Экстремум функции двух переменных

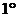Локальный экстремум

Окрестностью точки 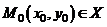называется круг, содержащий точку .

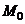Точка 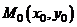называется точкой локального максимума (минимума) функции 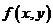, если существует окрестность точки 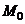, в которой для любой точки 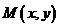выполняется неравенство

.

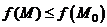
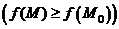Точки локального максимума и локального минимума называются точками локального экстремума.

Необходимое условие локального экстремума формулируется следующим образом.

Если функция 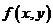имеет частные производные первого порядка в точке локального экстремума 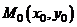, то

.

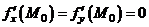Итак, «подозрительными» на экстремум являются те точки 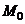, в которых все частные производные первого порядка обращаются в нуль. Такие точки называются стационарными.

Сформулируем достаточные условия экстремума функции двух переменных.

Пусть функция 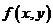имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки .

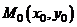Положим .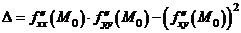

Тогда:

1) если 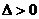, то в точке 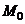функция имеет локальный экстремум, причём при 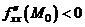- локальный максимум, при 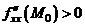- локальный минимум;

2) если 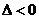, то в точке 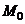нет экстремума;

3) если 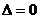, то вопрос о наличии экстремума остаётся открытым.

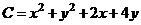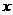Пример 23. Функция полных издержек двух продуктовых фирм задана уравнением , где и 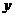- объёмы выпуска товаров 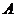и 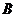соответственно. Цены этих товаров на рынке равны 8 и 6. Определить максимально возможное значение прибыли.

Решение

Найдём значение прибыли от реализации товара 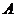и 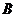в объёмах 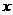и 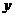как разность между доходом от продажи 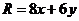и издержками .

.

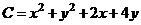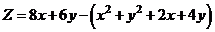Определим стационарные точки функции. Найдём частные производные:

, .

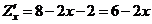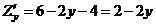Решим систему:

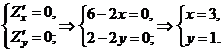
Точка 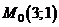- стационарная точка функции.

Найдём частные производные второго порядка:

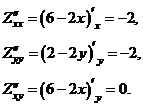
Учитывая что 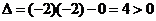, а 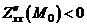, определим: 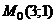- точка максимума. Найдём максимальное значение прибыли .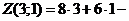

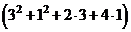
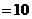Условный экстремум

Экстремум функции 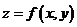при условии, что 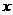и 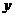связаны уравнением 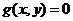, называется условным экстремумом. Уравнение 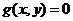называется уравнением связи.

Для решения задач на условный экстремум обычно используется метод Лагранжа.

Составим вспомогательную функцию

.

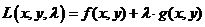Функция 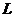называется функцией Лагранжа, а 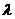- множителем Лагранжа.

Точка условного экстремума является точкой локального экстремума функции Лагранжа , её координаты должны удовлетворять уравнениям

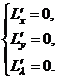
Пусть 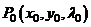- любое решение этой системы и

.

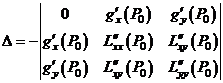Если 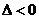, то функция 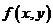имеет в точке 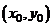условный максимум, если 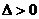, то условный минимум.

Пример 24. Найти экстремум 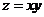при условии .

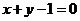Решение

Функция Лагранжа имеет вид .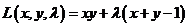

Найдём частные производные

.

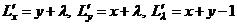Решим систему

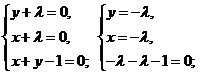
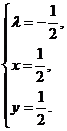
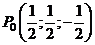- «подозрительная» точка.

Наёдем частные производные

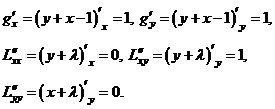
Вычислим определитель

.

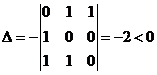В точке 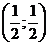функция 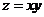имеет условный экстремум

.

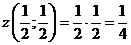Метод наименьших квадратов

Пусть имеются данные наблюдений в 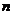точках 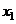, , 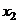, 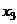…, 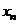некоторой величины 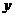и получены соответствующие значения , , , …, .

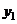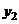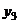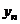Необходимо подобрать функцию определённого вида 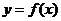, чтобы она по возможности наиболее точно отражала общую зависимость измеряемой величины 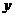от параметров (координат) точек измерения .

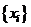При обработке данных экономической статистики наиболее распространённым является приближение эмпирической формулой в виде линейной функции одной переменной .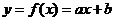

Неизвестные параметры эмпирической функци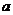и и 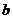необхо­димо определить так, чтобы значения функции 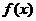по возможности наименее всего отклонялись от измеренных значений.

Метод наименьших квадратов состоит в минимизации суммы квадратов отклонений 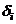функции 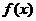в точках 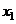, , 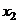, 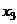…, 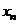от изме­ренных значений , , , …, .

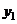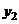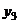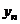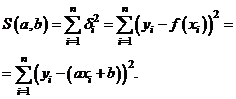
Для нахождения точки минимума функции 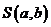найдём частные производные этой функции по переменным 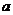и 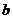и приравняем их к нулю.

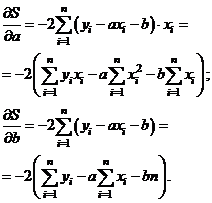
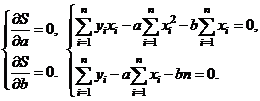
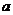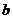Коэффициенты и определяются из системы так называемых нормальных уравнений.

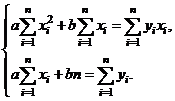
Пример 25. В результате эксперимента для пяти значений аргумента 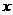получены пять значений величины .

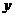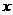	-2
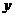	0,5		1,5

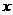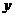Методом наименьших квадратов найти функциональную зависи­мость между и в виде линейной функции .

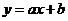Решение

Значение параметров 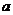и 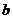найдём из системы . Выполним необходимые вычисления:

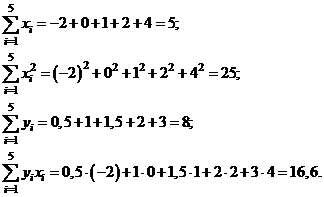
Запишем систему:

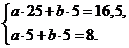
Решим систему по формулам Крамера:

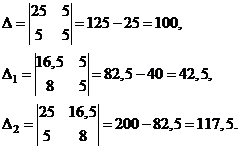
Значит , .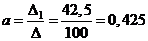

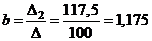Функция имеет вид 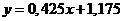.