Понятие определённого интеграла. Формулы Ньютона-Лейбница
Пусть функция 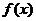 определена на отрезке
определена на отрезке  ,
,  . Разобьём отрезок на
. Разобьём отрезок на 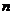 произвольных частей точками
произвольных частей точками 

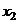

 . В каждом из полученных частичных отрезков выберем произвольную точку
. В каждом из полученных частичных отрезков выберем произвольную точку  и составим сумму
и составим сумму

где  - длина частичного отрезка.
- длина частичного отрезка.
Сумма вида называется интегральной суммойдля функции  на
на  . Обозначим через
. Обозначим через 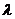 длину наибольшего частичного отрезка разбиения.
длину наибольшего частичного отрезка разбиения.
Если существует конечный предел интегральной суммы при  , этот предел называется определённым интегралом от функции
, этот предел называется определённым интегралом от функции  по отрезку
по отрезку  . Обозначается
. Обозначается 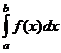 , а сама функция
, а сама функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке  . Итак
. Итак
 .
.
Числа 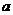 и
и 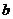 называются нижним и верхним пределами интегрирования,
называются нижним и верхним пределами интегрирования,  - подынтегральная функция,
- подынтегральная функция, 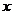 - переменная интегрирования.
- переменная интегрирования.
К понятию определённого интеграла мы приходим, например, при рассмотрении задачи о нахождении объёма продукции некоторого производства.
Пусть функция  описывает изменение производительности некоторого производства с течением времени
описывает изменение производительности некоторого производства с течением времени  . Для нахождения объёма продукции
. Для нахождения объёма продукции  , произведённый за промежуток времени
, произведённый за промежуток времени  , разобьём отрезок
, разобьём отрезок  на промежутки
на промежутки  . Тогда величину объёма продукции
. Тогда величину объёма продукции  , произведённой за промежуток времени
, произведённой за промежуток времени  найдём по формуле
найдём по формуле
 ,
,
где  ,
,  ,
,  .
.
 .
.
Точное равенство мы получим, переходя к пределу при 
 .
.
 .
.
Учитывая определение определённого интеграла, получим  , то есть если
, то есть если  - производительность труда в момент времени
- производительность труда в момент времени  , то
, то  - объём выпускаемой продукции за промежуток
- объём выпускаемой продукции за промежуток  .
.
Достаточным условием интегрируемости функции  на отрезке
на отрезке  является её непрерывность на этом отрезке.
является её непрерывность на этом отрезке.
Если  непрерывна на
непрерывна на  и функция
и функция  является некоторой её первообразной на этом отрезке, то имеет место формула Ньютона-Лейбница
является некоторой её первообразной на этом отрезке, то имеет место формула Ньютона-Лейбница
 .
.
То есть определённый интеграл от функции  на
на  равен приращению первообразной
равен приращению первообразной  на этом отрезке.
на этом отрезке.
Пример 9. Вычислить интеграл  .
.
Решение
Так как одной из первообразных для функции  является
является  , то применяя формулу , получим
, то применяя формулу , получим
 .
.
Основные свойства определённого интеграла
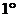 По определению
По определению  .
.
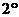 По определению
По определению  .
.
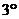 Каковы бы ни были числа
Каковы бы ни были числа  , всегда имеет место равенство
, всегда имеет место равенство  .
.
 Постоянный множитель можно выносить за знак определённого интеграла, т.е.
Постоянный множитель можно выносить за знак определённого интеграла, т.е.  .
.
 Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов
Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов
 .
.
Пример 10. Вычислить интеграл  .
.
Решение




 .
.
 Интеграл от неотрицательной функции на отрезке
Интеграл от неотрицательной функции на отрезке  - неотрицательное число, то есть если
- неотрицательное число, то есть если  на
на  , то
, то  .
.
 Если на
Если на  выполняется неравенство
выполняется неравенство  , то такое же неравенство выполняется и для интегралов, т.е.
, то такое же неравенство выполняется и для интегралов, т.е.
 .
.
 Пусть
Пусть  - наименьшее, а
- наименьшее, а  - наибольшее значения непрерывной функции
- наибольшее значения непрерывной функции 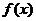 на
на  , тогда
, тогда
 .
.
Пример 11. Оценить определённый интеграл  .
.
Решение
Функция  убывает на промежутке
убывает на промежутке  , поэтому
, поэтому  ,
,  . Значит
. Значит  ,
,  .
.
 Если
Если 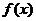 непрерывна на отрезке
непрерывна на отрезке  , то найдётся такое значение
, то найдётся такое значение  , что
, что  .
.
 - среднее значение функции
- среднее значение функции 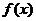 на отрезке
на отрезке  .
.
При вычислении определённых интегралов применяют также метод замены переменной, который позволяет упростить интеграл. При этом в отличие от неопределённого интеграла нет необходимости возвращаться к исходной переменной интегрирования. Достаточно найти пределы интегрирования новой переменной и воспользоваться формулой Ньютона-Лейбница.
Формула замены переменной в определённом интеграле имеет вид
 .
.
Пример 12. Вычислить интегралы:
а)  ; б)
; б)  .
.
Решение
а) 



 .
.
б) 




 .
.
Формула интегрирования по частям в определённом интеграле имеет вид
 .
.
Пример 13. Вычислить интеграл  .
.
Решение



 ,
,
так как  ,
,  .
.
