Тема 1: Выборочное наблюдение.
при решении задач по данной теме примем некоторые обозначения.
N – объем генеральной совокупности (число входящих в нее единиц);
n – объем выборки (число обследованных единиц);
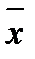 - генеральная средняя (среднее значение признака в генеральной совокупности);
- генеральная средняя (среднее значение признака в генеральной совокупности);
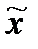 – выборочная средняя;
– выборочная средняя;
p – генеральная доля (доля единиц, обладающих данным значением признака, в общем числе единиц генеральной совокупности), например, доля числа бракованных единиц в общем количестве единиц в данной партии изделий;
w – выборочная доля;
s2 – генеральная дисперсия (дисперсия признака в генеральной совокупности);
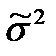 – выборочная дисперсия того же признака;
– выборочная дисперсия того же признака;
s - среднее квадратическое отклонение в генеральной совокупности;
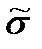 – среднее квадратическое отклонение в выборке.
– среднее квадратическое отклонение в выборке.
Между характеристиками выборочной совокупности и искомыми характеристиками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой выборки.
Задачи, решаемые в этой теме, обусловлены практическими вопросами, требующими своего решения при организации выборочного наблюдения и анализе его результатов. Такими вопросами являются определение способа отбора и процедуры выборки; вычисление ошибок выборки и построение доверительных интервалов выборочных характеристик, а также расчетов необходимого объема выборки.
Различают среднюю и предельную ошибки выборки. Эти два вида ошибок связаны следующим соотношением:
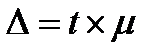
где Δ – предельная ошибка выборки;
μ – средняя ошибка выборки;
t – коэффициент доверия, определяемый в зависимости от уровня вероятности (Приложение 4).
Предельные ошибки выборки (  ) определяются в зависимости от метода отбора по формулам:
) определяются в зависимости от метода отбора по формулам:
| Метод отбора | Формулы объема выборки | |
| Для средней | Для доли | |
| Повторный | 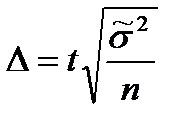 | 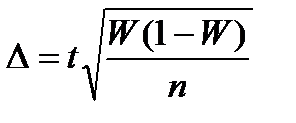 |
| Бесповторный | 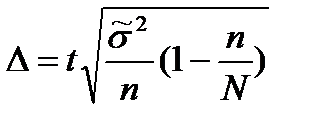 | 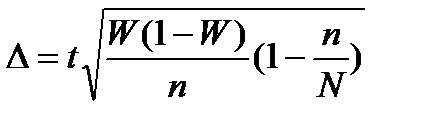 |
После вычисления предельных ошибок выборки находят доверительные интервалы для генеральных показателей. Для `Х это ( 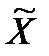 ± Δх). Для Р это (W ± Δw), т.е.
± Δх). Для Р это (W ± Δw), т.е.
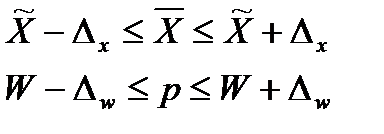
Доля признака (W=m/n) – доля единиц, обладающих определенным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Дисперсия доли находится следующим образом:
σw2 = W*(1 - W)
Формулы, приведенные выше, используются при определении ошибок выборки и объема выборочной совокупности, осуществляемой собственно случайным или механическим методами. В случае с типической выборкойпоказателем вариации является средняя из внутригруппировочных дисперсий 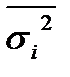 ; при серийной выборке - межгрупповая (межсерийная) дисперсия δ2 , а N и n заменяются на R и r – число серий в генеральной и выборочной совокупности соответственно.
; при серийной выборке - межгрупповая (межсерийная) дисперсия δ2 , а N и n заменяются на R и r – число серий в генеральной и выборочной совокупности соответственно.
· Для типической выборки предельная ошибка вычисляет следующим образом:
- при отборе, пропорциональном объему типических групп:

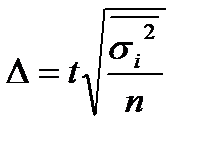 - повторный отбор,
- повторный отбор,
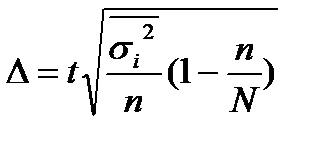 - бесповторный отбор.
- бесповторный отбор.
- при отборе, пропорциональном вариации признака (непропорциональном объему типических групп):
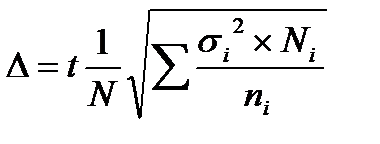 - повторный отбор,
- повторный отбор,
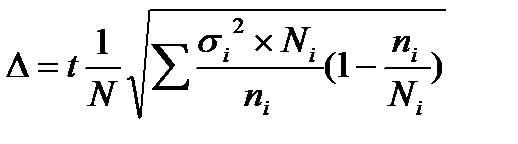 - бесповторный отбор,
- бесповторный отбор,
где Ni и ni – объемы i-ой типической группы и выборки из нее соответственно,
 i2 – групповые дисперсии.
i2 – групповые дисперсии.
· При серийной выборке предельная ошибка определяется:
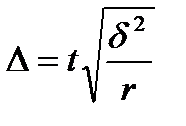 - повторный отбор,
- повторный отбор,
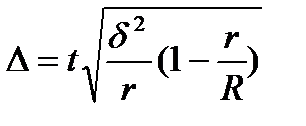 - бесповторный отбор,
- бесповторный отбор,
где R и r – число серий в генеральной и выборочной совокупности соответственно,
δ2 – межгрупповая (межсерийная) дисперсия, которая находится по следующей формуле:
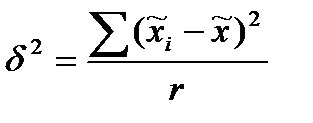
где 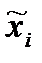 - серийные средние,
- серийные средние,
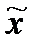 - общая средняя.
- общая средняя.
Разрабатывая программу выборочного наблюдения, задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Формулы для определения численности выборки (n) зависят от метода отбора. Они различны для расчета средней и доли и следуют из формул предельных ошибок выборки:
| Метод отбора | Формулы объема выборки | |
| Для средней | Для доли | |
| Повторный | 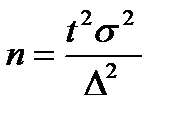 | 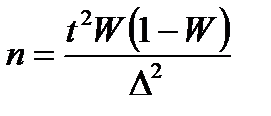 |
| Бесповторный | 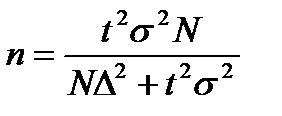 | 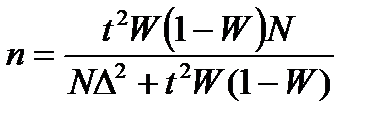 |
При определении численности типических групп в выборке применяются формулы:
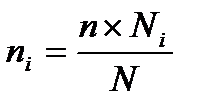
Рассмотрим примеры решения типовых задач:
Задание 1.В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
| Число детей в семье | ||||||
| Количество семей | 1 000 | 2 000 | 1 200 |
С вероятностью 0,954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение:
Вначале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
| Xi | fi | Xifi | Xi - 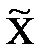 | (Xi - 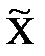 )2 )2 | (Xi - 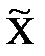 )2 fi )2 fi |
| -1.5 | 2.25 | ||||
| -0.5 | 0.25 | ||||
| 0.5 | 0.25 | ||||
| 1.5 | 2.25 | ||||
| 2.5 | 6.25 | ||||
| 3.5 | 12.25 | ||||
| Итого | - | - |
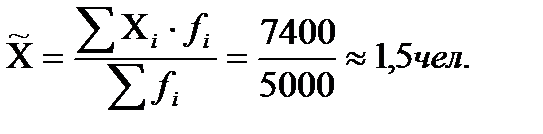
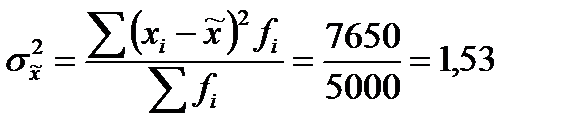
Вычислим теперь предельную ошибку выборки:
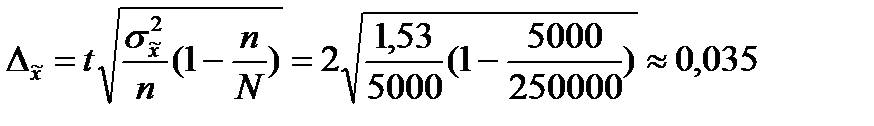
Следовательно, пределы генеральной средней 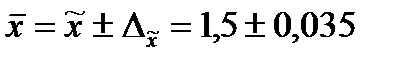
Таким образом, с вероятностью 0.954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1.5, т.е. в среднем на каждые две семьи приходится три ребенка.
Задание 2.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?
Дано: N=100 P=0,683 t= 1  =3 =3 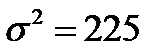 |
Найти: n.
Решение: 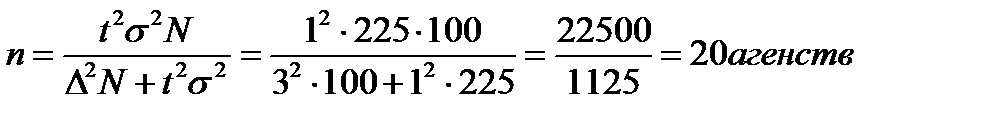
Вывод: Таким образом, требуется обследовать 20 агентств в городе, чтобы с вероятностью 0.683 ошибка не превысила трех путевок.
Задачи для самостоятельного решения:
Задача 1.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.
Задача 2.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек в июне 1996 г. была проведена 25 %-ная механическая выборка. По результатам наблюдения оказалось, что у 10 % обследованных потери времени достигали более 45 минут в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Задача 3.
Задача 4.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили: 14,5 ц/га, 16,0 ц/га, 15,5 ц/га,15,0 ц/га, 14,0 ц/га. С вероятности 0,954 найдите пределы урожайности по всей совокупности.
Задача 5.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин. На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке равной 5 человек.
Задача 6.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5.
Задача 7.
При обследовании качества завозимых в регион в зимний период фруктов и овощей была организована 20%-ая типическая пропорциональная выборка. Результаты в таблице:
| Наименование группы | Объем выборки, кг | Доля испорченного товара, % |
| Овощи | ||
| Фрукты |
С вероятностью 0,954 установите границы доли испорченного товара.
Задача 8.
С целью определения средних затрат времени при поездках на работу населением города планируется выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 мин. при среднем квадратическом отклонении 15 мин?
Задача 9.
На АО «Машиноаппарат» 2400 станков, в т.ч. токарных – 960, фрезерных – 720, шлифовальных – 480, прочих – 240. С целью исследования производительности станков планируется организовать типическую пропорциональную выборку станков с механическим отбором внутри групп. По результатам аналогичного исследования на другом подобном предприятии среднее квадратическое отклонение составило 60. Сколько станков необходимо отобрать из каждой группы, чтобы ошибка выборки не превышала 20 единиц при вероятности 0,997?
Задача 10.
Для обследования всхожести семян они были распределены на 50 равновеликих серий. На основе механического отбора было проверено 10 серий, в которых удельный вес взошедших семян составил 80%. С вероятностью 0,683 установите границы доли всхожести семян во всей партии, если межсерийная дисперсия равна 841.
Задача 11.
В процессе подготовки выборочного обследования качества импортируемых кондитерских изделий была проведена пробная проверка 8 ящиков для сбора данных о вариации их веса. Результаты проверки в таблице:
| № ящика | ||||||||
| Сред.вес короб-ки в ящике, г |
Сколько ящиков необходимо отобрать для проверки качества в порядке бесповторного отбора, чтобы с вероятностью 0,997 ошибка выборки не превышала20 г, если генеральная совокупность включает 1000 равных по величине серий?
Задача 12.
На площади в 50 га, занятой пшеницей, определяется с помощью выборочного метода доля посева, пораженная насекомыми-вредителями. Сколько проб надо взять в выборку, чтобы при вероятности 0,997 определить искомую величину с точностью до 3 %, если пробная выборка показывает, что доля пораженной посевной площади составляет 6 %?
Задача 13.
Партия электроламп упакована в 200 коробок по 100 шт. в каждой. Средняя длительность горения электроламп составляет 1150ч, а межсерийная дисперсия - 200. Качество электроламп проверяется на основе серийного 3%-ного случайного бесповторного отбора. Определите: а) предельную ошибку при установлении средней длительности горения электроламп; б) пределы контролируемого параметра в генеральной совокупности. Выводы сделайте с вероятностью 0,954.
Задача 14.
На предприятии было проведено повторное обследование стажа работы у 12 мужчин и 8 женщин. Результаты в таблице:
| Группа рабочих | Кол-во, чел. | Сред.стаж, лет | Сред.кв.отклонение |
| Мужчины | |||
| Женщины |
Рассчитать общий средний стаж работы по выборочным данным. С вероятностью 0,954 определить доверительные пределы среднего стажа работы в генеральной совокупности.
Задача 15.
На предприятии, на котором работает 250 человек, было проведено обследование размера заработной платы. Результаты в таблице:
| Группа рабочих | Кол-во, чел. | Сред.з/п, руб | Сред.кв.отклонение |
| Мужчины | |||
| Женщины |
Рассчитать общую среднюю зарплату по выборочным данным. С вероятностью 0,997 определить доверительные пределы средней зарплаты в генеральной совокупности и среднюю ошибку выборочной средней.
Задача 16.
На предприятии с числом установленных металлорежущих станков 120 единиц необходимо на основе выборочного обследования определить долю станков возрастом свыше 10 лет. Никаких предварительных данных об удельном весе этого оборудования в общей численности установленного оборудования нет.
Определить, каков должен быть объем выборки механическим отбором, чтобы при вероятности 0,954 предельная ошибка выборки не превышала 5%.
