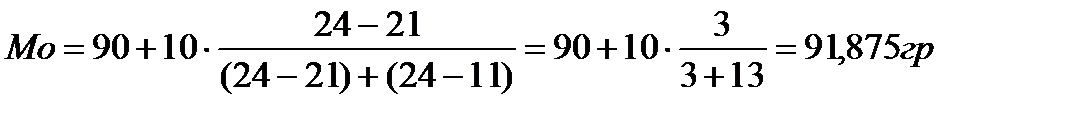Тема 2: Абсолютные, относительные и средние величины. Показатели вариации.
Результаты статистического наблюдения регистрируются прежде всего в форме первичных абсолютных величин.
В статистике все абсолютные величины являются именованными, измеряются в конкретных единицах (человеках, рублях, штуках, киловатт-часах, человеко-днях и человеко-часах и т.д.) и, в отличие от математического понятия абсолютной величины, могут быть как положительными, так и отрицательными (убытки, убыль, потери и т.п.)
Поскольку абсолютные показатели – это основа всех форм учета и приемов количественного анализа, то следует разграничивать моментные и интервальные абсолютные величины. Первые показывают фактическое наличие или уровень явления на определенный момент, дату (например, наличие запасов материалов или оборотных средств, величина незавершенного производства, численность проживающих и т.д.). Вторые – итоговый накопленный результат за период в целом (объем произведенной продукции за месяц или год, прирост населения за определенный период, величина валового сбора зерна за год и за пятилетку и т.д.)
Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин.
Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа.
Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины произвольные, определяемые в форме коэффициентов, процентов, промилле и т.д.
Относительные величины образуют систему взаимосвязанных статистических показателей. По содержанию выражаемых количественных соотношений выделяют следующие типы относительных величин.
Относительный показатель динамики. Характеризует изменение уровня развития какого-либо явления во времени. Получается в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент.
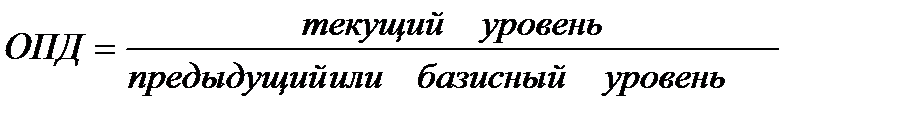
Относительный показатель плана. Рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предшествующем периоде.
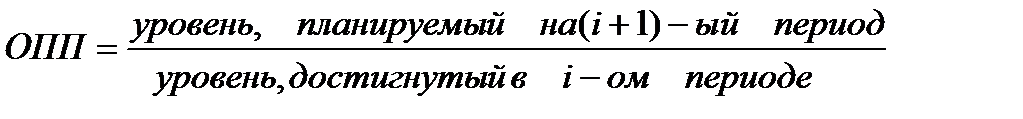
Относительный показатель реализации плана. Рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному.
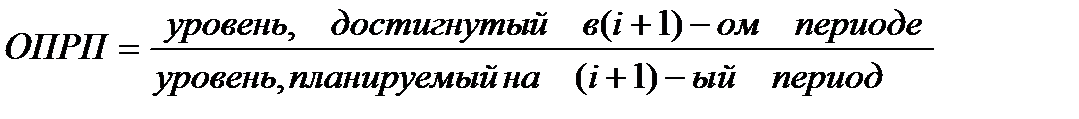
Между этими показателями существует взаимосвязь: ОПП * ОПРП = ОПД
Относительный показатель структуры. Характеризуют доли, удельные веса составных элементов в общем итоге. Как правило, их получают в форме процентного содержания:
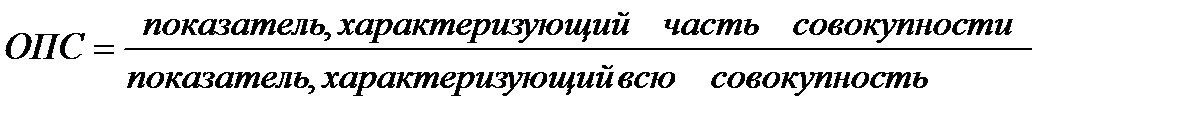
Относительный показатель координации. Характеризуют отношение частей данной совокупности к одной их них, принятой за базу сравнения. ОПК показывают, во сколько раз одна часть совокупности больше другой, либо сколько единиц одной части приходится на 1, 10, 100, 1000, … единиц другой части. Относительные величины координации могут рассчитываться и по абсолютным показателям, и по показателям структуры.
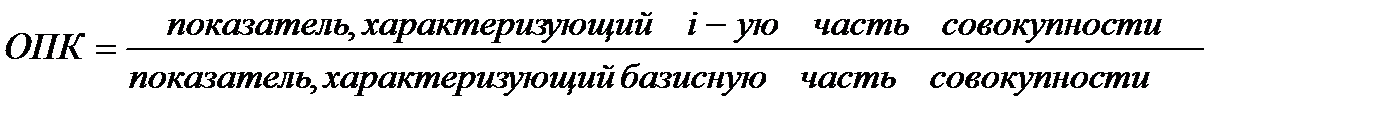
Относительный показатель интенсивности. Характеризуют степень распределения или развития данного явления в той или иной среде. Представляют собой отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком.
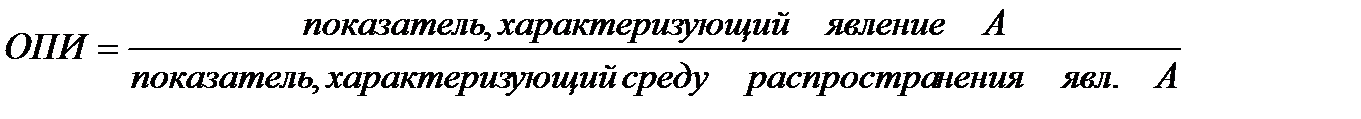
Относительный показатель сравнения. Характеризуют сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям.
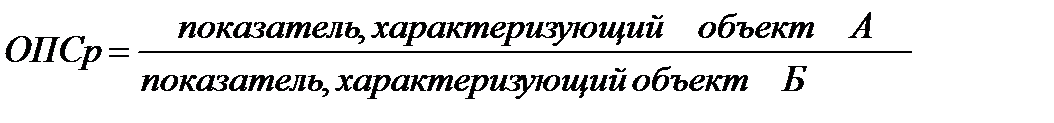
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Средние величины делятся на два больших класса: степенные средние и структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
Табл. 1Виды степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | ||
| Простая | Взвешенная | |||
| Гармоническая | -1 | 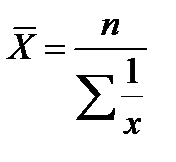 | 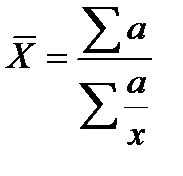 a = xf a = xf | |
| Геометрическая | 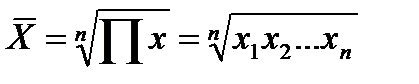 | 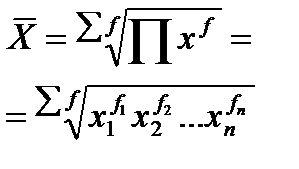 | ||
| Арифметическая | 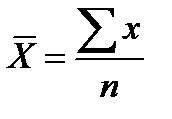 | 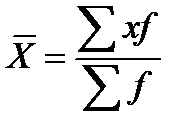 | ||
| Квадратическая | 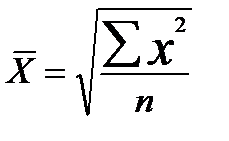 | 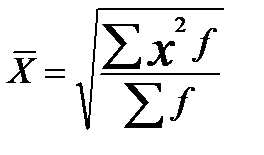 | ||
| Кубическая | 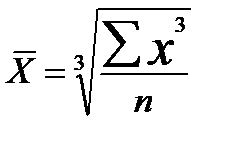 | 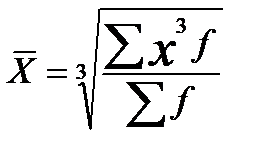 |
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.
Как выбрать какую среднюю рассчитывать арифметическую или гармоническую?
В.Е. Овсиенко1 формализовал порядок выбора формы средней качественного признака на основе следующих правил:
1. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должна вычисляться по формуле средней арифметической взвешенной.
2. Если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической.
3. В том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя вычисляется непосредственно по этой формуле.
Следует также отметить, что средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. a = Xf).
Рассмотрим пример расчета степенных средних.
Пример 1.По данным таблицы рассчитать среднюю заработную плату в целом по трем предприятиям.
Табл.
| Предприятие | Численность промышленно-производственного персонала, чел | Месячный фонд з/п, тыс. руб. | Средняя з/п, руб. |
| 5648,4 | |||
| 3327,5 | |||
| 5175,4 | |||
| Итого | 14151,3 | ? |
Решение:
Для нахождения средней определим исходное соотношение средней для показателя «Средняя зарплата». Независимо от имеющихся в нашем распоряжении данных средняя зарплата может быть получена только чрез следующее отношение:
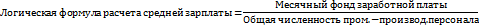
1. Предположим, что мы располагаем данными только граф 1 и 2 («Численность промышленно–производственного (ППП) персонала» и «Месячный фонд зарплаты»). Итоги этих граф содержат необходимые величины для расчета искомой средней величины по ее логической формуле:
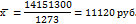
Следовательно, средняя зарплата по трем предприятиям составляет 11120 руб.
2. Если мы располагаем только данными граф 1 и 3 («Средняя зарплата» и «Численность ППП»), то нам известен знаменатель логической формулы, но не известен ее числитель (однако фонд заработной платы можно получить умножением средней зарплаты на численность ППП). Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
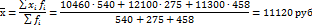
где 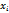 - средняя заработная плата на каждом предприятии, руб.
- средняя заработная плата на каждом предприятии, руб.
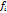 - численность промышленно-производственного персонала, чел.
- численность промышленно-производственного персонала, чел.
3. Если мы располагаем только данными граф 2 и 3 ( “Месячный фонд з/п” и “Средняя з/п”), то нам известен числитель логической формулы, но не известен ее знаменатель (однако численность можно получить разделив фонд заработной платы на среднюю зарплату на каждом предприятии). Следовательно общая средняя может быть рассчитана по формуле средней гармонической взвешенной:

где 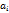 - это месячный фонд з/ п на каждом предприятии, руб.,
- это месячный фонд з/ п на каждом предприятии, руб.,
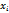 - средняя зарплата на каждом предприятии, руб.
- средняя зарплата на каждом предприятии, руб.
Следовательно, средняя зарплата по трем предприятиям составляет 11120 руб.
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы– величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Для интервального ряда расчет моды и медианы проводится по следующим формулам.
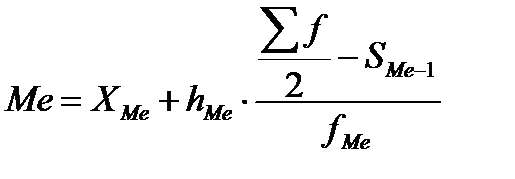 ,
,
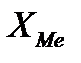 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
hMe- его величина;
Σf/2  - половина суммы частот;
- половина суммы частот;
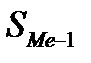 - накопленная частота, предшествующая медианному интервалу;
- накопленная частота, предшествующая медианному интервалу;
fMe- число наблюдений или объем взвешивающего признака в медианном интервале (частота медианного интервала).
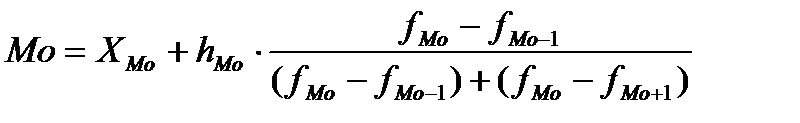 ,
,
где XMo- нижняя граница модального интервала;
fMo- частота модального интервала;
fMo-1 - частота интервала, предшествующего модальному;
fMo+1 - частота интервала, следующего за модальным;
hMo – величина модального интервала.
ПОКАЗАТЕЛИ ВАРИАЦИИ.
Вариация-это колеблемость, многообразие, изменяемость значений признака у единиц совокупности, т.е. несовпадение уровней одного и того же показателя у разных объектов. Вариация имеет объективный характер и помогает познать сущность изучаемого явления.
Для измерения вариациив статистике применяют несколько способов.
Наиболее простым является расчет показателя размаха вариацииH как разницы между максимальным (Xmax) и минимальным (Xmin) наблюдаемыми значениями признака:
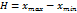
Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение 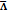 как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
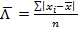 - невзвешенное среднее линейное отклонение,
- невзвешенное среднее линейное отклонение,
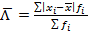 - взвешенное среднее линейное отклонение
- взвешенное среднее линейное отклонение
Дисперсияпризнака ( 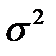 ) определяется на основе квадратической степенной средней:
) определяется на основе квадратической степенной средней:
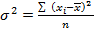 или
или 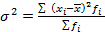 .
.
Показатель s, равный 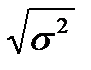 , называется средним квадратическим отклонением.
, называется средним квадратическим отклонением.
Если первичные данные сгруппировать, то дисперсия признака может быть определена как сумма так называемой межгрупповой дисперсии – δ2 и среднего значения внутригрупповых дисперсий - 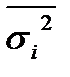 , т.е. по правилу сложения дисперсий:
, т.е. по правилу сложения дисперсий:
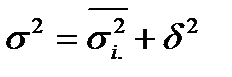 .
.
Mежгрупповая дисперсия рассчитывается как
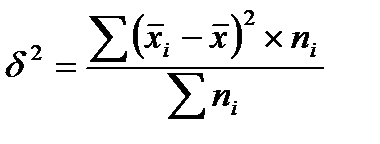 ,
,
где 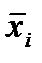 - среднее значение признака по группе i;
- среднее значение признака по группе i;
ni – численность группы i;
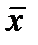 - общее среднее значение признака.
- общее среднее значение признака.
Средняя из внутригрупповых дисперсий рассчитывается по формуле
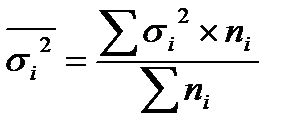 ,
,
где 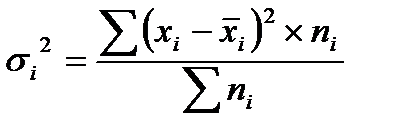 - групповая дисперсия.
- групповая дисперсия.
При расчете относительных показателей вариации базой для сравнения служит средняя арифметическая. Эти показатели дают характеристику однородности совокупности. К ним относятся:
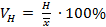 - коэффициент осцилляции,
- коэффициент осцилляции,
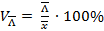 - линейный коэффициент вариации,
- линейный коэффициент вариации,
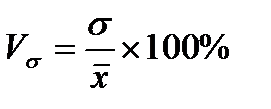 - коэффициент вариации.
- коэффициент вариации.
Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Рассмотрим пример расчета показателей:
Пример 2. Имеются следующие данные о весе изготавливаемых деталей:
| Группы деталей по весу, г | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | Итого |
| Число деталей |
По данным таблицы рассчитать: 1) средний вес деталей, 2) моду и медиану; 3) размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Решение:
Табл. Промежуточные расчеты
| Группы деталей по весу, г | 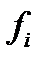 | 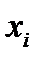 | 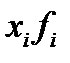 | 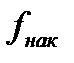 | 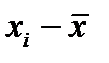 | 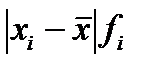 | 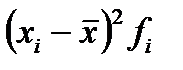 |  |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 40 – 50 | -40,8 | 81,6 | 3329,3 | -135 834,6 | 5 542 052,7 | ||||
| 50 – 60 | -30,8 | 123,2 | 3794,6 | -116 872, 5 | 3 599 671,4 | ||||
| 60 – 70 | -20,8 | 249,6 | 5191,7 | -107 986,9 | 2 246 128,4 | ||||
| 70 – 80 | -10,8 | 194,4 | 2099,5 | -22 674,8 | 244 888,0 | ||||
| 80 – 90 | -0,8 | 16,8 | 13,44 | -10,8 | 8,6 | ||||
| 90 – 100 | 9,2 | 220,8 | 2031,4 | 18 688,5 | 171 934,3 | ||||
| 100–110 | 19,2 | 211,2 | 4055,0 | 77 856,8 | 1 494 849, 9 | ||||
| 110-120 | 29,2 | 233,6 | 6821,1 | 199 176, 7 | 5 815 959,8 | ||||
| Итого | - | - | - | 1331,2 | 27 336,0 | -87 657,6 | 19 115 493, 1 |
1) Рассчитаем средний уровень ряда (так как имеются значения осредняемого признака и частота с которой они встречаются в совокупности – вариационный ряд распределения, то средний вес детали определяем по формуле средней арифметической взвешенной):
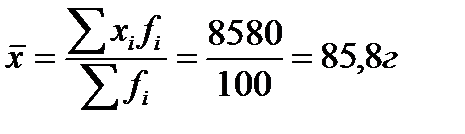
Следовательно средний вес деталей в партии составляет 85,8 гр.
2) Определим моду и медиану аналитическим способом: Находим максимальную частоту в ряду распределения – в рассматриваемом примере она равна 24 (f max= 24) и соответствует интервалу (90-100), следовательно 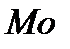 будет находиться в интервале от 90 до 100. Определяем параметры для подстановки в формулу моды:
будет находиться в интервале от 90 до 100. Определяем параметры для подстановки в формулу моды:
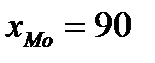 ; h = 10;
; h = 10; 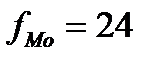 ;
; 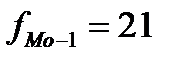 ;
; 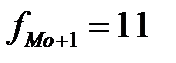 .
.