Сравнение бесконечно малых, основные теоремы

Говорят, что a(x) – бесконечно малая более высокого порядка малости, чем b(x), если 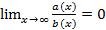, (в случае, если поменять местами, будет бесконечность).

Говорят, что они имеют одинаковый порядок малости, если данный предел будет равняться вещественному числу.

Говорят, что их порядок малости одинаковый, если данный предел будет равен 1.

1.

2.

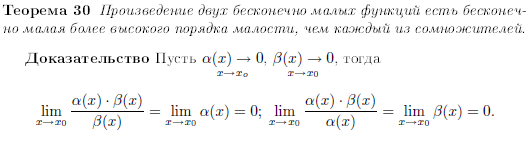
3.

Основные теоремы о пределах

1. О пределах в равенстве, если g(x)=f(x), то их пределы равны.

2. О пределах в неравенстве, было доказано ранее.

3. Предел постоянной равен постоянной.

4. Единственность предела, было доказано ранее.

5.

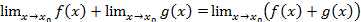
Доказательство: Пускай, пределы f(x)=aи g(x)=b – бесконечно малые.

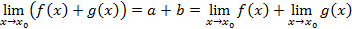
6. Аналогично с произведением.

7. Аналогично с частным.

Существование предела однородной последовательности

Материал не найден

Критерий Коши существования предела

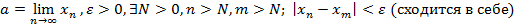
Замечательные пределы

Первый замечательный предел: .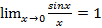

Второй замечательный предел: .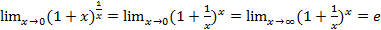

Непрерывность функции в точке, определение и теоремы

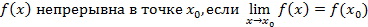
Вариант по Коши:

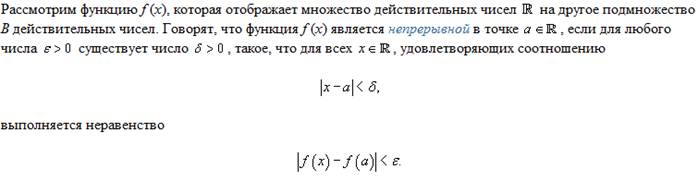
Теоремы:

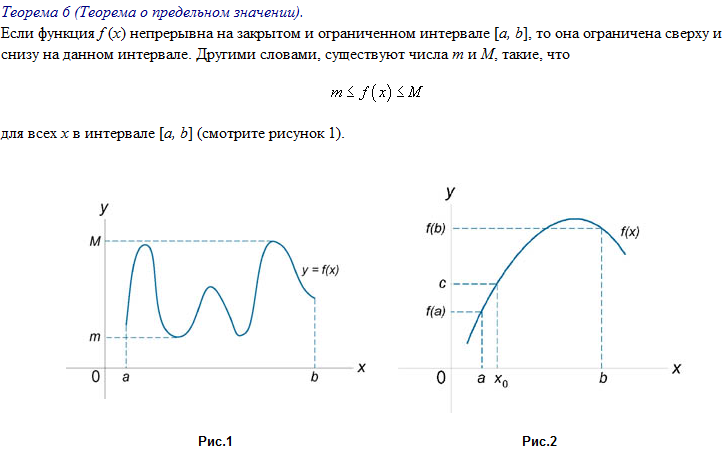
Односторонний предел, односторонняя непрерывность

В формуле предела по Коши:

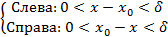
Предел, который стремится своему значению только с одной стороны.

В таком случае, для конечных пределов справа\слева есть конечная непрерывность справа\слева.

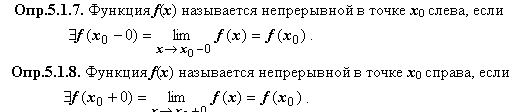
Классификация разрывов

Первого порядка: предел справа и предел слева конечны. Функция визуально имеет «угол».

Второго порядка: если хотя бы один предел стремится кплюс\минус бесконечности или не существует. Функция визуально «разорвана».

Свойства функции, непрерывной на отрезке

Производная, непрерывность имеющей производную функции

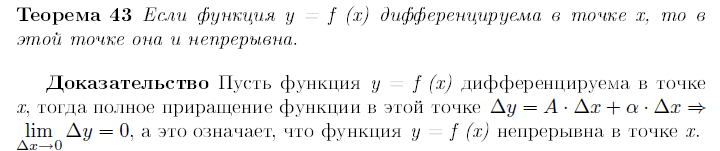
Таблица производных, правила дифференцирования

17)Дифференциал, дифференцируемость функции, инвариантность первого дифференциала

Дифференциалом называется произведение f’(x)dx, или dy.

Дифференциал – линейная часть приращения функции.

Производные и дифференциалы старших порядков

Вторая производная является производной более старшего порядка, чем первая.

Аналогично и с дифференциалами. Дифференциал старшего порядка просто найти по данной формуле: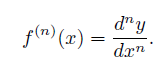

Дифференциал порядка старше 2 неинвариантен.

Дифференцирование функций, заданных параметрически и неявно

Параметрически. Представим себе yи xкак сложные функции от t. Продифференцируем.

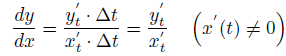
В таком случае, второй дифференциал:

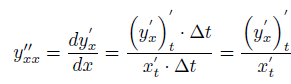
Неявные функции. В таком случае, берётся производная от неявной функции так же, как и от стандартной. От yберётся производная так же, как и от x, но каждый раз домножается на y’ (как будто берётся производная по сложной функции).

Теоремы Ферма и Ролля

Ролля

Для прямолинейной функции это доказывается просто. Докажем для непрямолинейной.

Ферма

Частный случай. Теорема гласит, что на приведённом выше промежутке есть максимум или минимум. Собственно говоря, если производная равна нулю, то это одно из двух, без доказательства.

Теоремы Лагранжа и Коши

Лагранж

Коши

Чисто в принципе, это – частный случай Лагранжа. По крайней мере, доказывается так же.

Вместе (b-a) и (x-a) в дополнительной функции мы записываем вторую функцию от этих аргументов, доказывая, что обе дроби в формуле Коши равны нулю.

Формулы Тейлора и Маклорена

Формула Тейлора имеет вид:

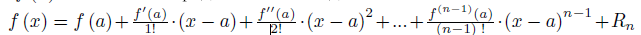
Формула Маклорена – её частный случай, в ней a=0.

Любую f(x) можно разложить по данной формуле.

R_n – остаточный член, его формула (по Лагранжу): 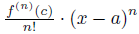.