Как определять тип дифференциального уравнения первого порядка
Ø Прежде всего, нужно знать типы всех уравнений и признаки каждого из них на память.
Ø Затем усвоить алгоритм распознавания типа дифференциального уравнения, который состоит из проверки признаков типов дифференциальных уравнений.
Ниже приводится сводная таблица типов дифференциальных уравнений первого порядка и их признаков.
| Тип | Название диф. ур-я | Общий вид | Признаки | Метод решения |
| I | Уравнение с разделяющимися переменными | 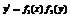 или или 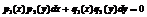 | В правой части (функции 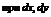 ) стоит произведение двух функций, каждая из которых зависит только от одной переменной ) стоит произведение двух функций, каждая из которых зависит только от одной переменной | Разделение переменных и интегрирование |
| II | Однородное уравнение | 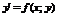 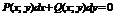 | 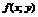 − однородная функция нулевого измерения; − однородная функция нулевого измерения; 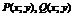 − однородные функции одного измерения − однородные функции одного измерения | 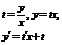 |
| III | 1. Линейное уравнение относительно 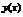 2. Линейное уравнение относительно 2. Линейное уравнение относительно 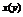 | 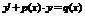 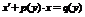 | Функция, ее производная входят в уравнение в первой степени (линейно) | 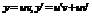 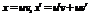 |
| IV | 1. Уравнение Бернулли относительно 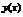 2. Уравнение Бернулли относительно 2. Уравнение Бернулли относительно 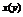 | 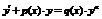 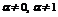 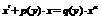 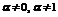 | Отличается от соответствующего линейного уравнения правой частью | Делим 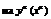 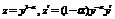 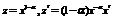 |
| V | Уравнение в полных дифференциалах | 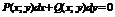 | 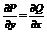 |
Как только данное уравнение совпадает по признакам (или общему виду) с одним из типов, его следует решать, воспользовавшись соответствующим этому типу методом.
Чтобы определить дифференциального уравнения, его лучше записать либо в виде
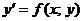 , либо
, либо 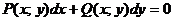 − как проще.
− как проще.
Дифференциальные уравнения второго порядка
Дифференциальное уравнение второго порядка имеет вид
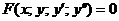 (2.1)
(2.1)
или
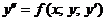 . (2.2)
. (2.2)
Общим решением уравнения (2.1) называется функция
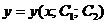 (2.3)
(2.3)
Эта функция зависит от переменной x и двух произвольных постоянных 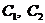 , обращает данное уравнение в верное равенство.
, обращает данное уравнение в верное равенство.
Общее решение уравнения (2.1), заданное в неявном виде
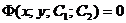 , (2.4)
, (2.4)
называется общим интегралом.
Частное решение
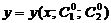 , (2.5)
, (2.5)
где 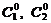 − фиксированные числа, получаются из общего решения (2.3) при фиксированных значениях
− фиксированные числа, получаются из общего решения (2.3) при фиксированных значениях  .
.
Задача Коши. Найти решение дифференциального уравнения (2.1), удовлетворяющее условиям: 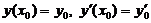 .
.
Константы  определяются из системы уравнений:
определяются из системы уравнений:
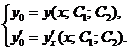 (2.6)
(2.6)
Дифференциальные уравнения второго порядка, допускающие
Понижение порядка
Рассмотрим три частных случая, когда решение уравнения (2.2) с помощью замены переменной сводится к решению уравнения первого порядка. Такие преобразования уравнения (2.2) называются понижением порядка.
Уравнения вида 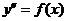
Уравнение не содержит 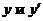 .
.
Уравнение интегрируется подстановкой 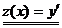 , которая дает возможность свести его к уравнению с разделяющимися переменными
, которая дает возможность свести его к уравнению с разделяющимися переменными 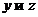 .
.
Уравнения вида 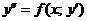
Уравнение не содержитy.
Положим, как и в предыдущем случае, 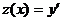 , тогда
, тогда 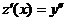 , и уравнение преобразуется в уравнение первого порядка относительно
, и уравнение преобразуется в уравнение первого порядка относительно 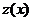 .
.
Уравнения вида 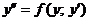
Уравнение не содержитx.
Вводим новую функцию 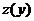 , полагая
, полагая 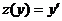 . Тогда
. Тогда
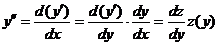 .
.
Подставляя в уравнение выражения 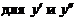 , получаем уравнение первого порядка относительно z как функции
, получаем уравнение первого порядка относительно z как функции 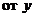 :
: 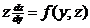 .
.
Ниже приводится сводная таблица трех типов дифференциальных уравнений второго порядка, допускающих понижение порядка, и их признаков.
| Тип | Вид уравнения | Признаки | Способ понижения порядка |
| А | 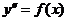 | Нет явно 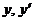 | Подстановка 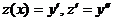 |
| Б | 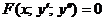 или или 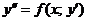 | Явно нет y | Подстановка 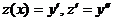 |
| В | 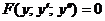 или или 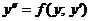 | Явно нет x | Подстановка 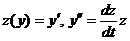 |
