Подходы к визуальному представлению уровня риска

5.1.1 Одномерное представление уровня риска на оценочной шкале

Самый простой подход к визуальному представлению уровня риска состоит в отображении точки риска на оценочной интервальной шкале, представляющей собой ось координат. Масштаб оси координат может быть как линейным, так и логарифмическим. При линейном масштабе границы областей значений риска отличаются на величину ΔR (рисунок 5.1а), а при логарифмическом – в K раз (рисунок 5.1б). Интервалам значений риска присваивается цветовой код в соответствии с рисунком 4.2. Теоретически, область значений риска, не принимаемого в расчет, ограничивается снизу только нулевым значением, а область значений недопустимого риска не ограничена сверху. Поэтому шкала может быть продолжена вниз (при условии, что значения больше 0) и вверх.

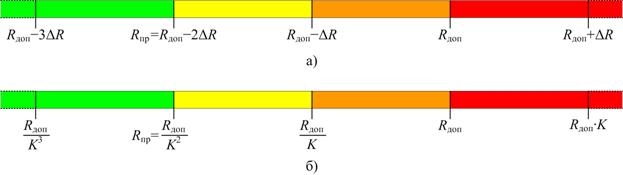
Рисунок 5.1 – Одномерное представление риска на осевой шкале рисков с линейным (а) и логарифмическим (б) масштабом

При применении линейного масштаба у шкалы возникает существенный недостаток: при расширении области значений риска, которую может отобразить шкала, шаг шкалы становится слишком большим и точки рисков с небольшим уровнем перестают различаться. Например, если задать шаг шкалы ΔR = 1000 ед., то точки рисков с уровнями 10 ед. и 50 ед. практически невозможно будет различить. Данный недостаток не присутствует в случае применения логарифмической шкалы. Но на логарифмических шкалах не может использоваться нулевое значение.

В таблице 5.1 приведен пример соотношения категорий риска с привязкой к допустимому уровню риска в случае логарифмического масштаба шкалы рисков.

Таблица 5.1 – Категории риска с привязкой к допустимому уровню

Категория риска	Диапазон значений
Недопустимый	R > Rдоп
Нежелательный	K-1·Rдоп ≤ R < Rдоп
Допустимый	K-2·Rдоп ≤ R < K-1·Rдоп
Не принимаемый в расчет	R < K-2·Rдоп

Также следует отметить, что в случае, когда жестко установлены R_доп и R_пр, шаги шкал ΔR (рисунок 5.1а) и K (рисунок 5.1б) не могут выбираться произвольными, а определяются следующими соотношениями:

, .

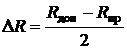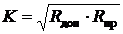(2)

К недостаткам данного подхода к представлению уровня риска следует отнести то, что одномерная шкала не дает информации о сочетании частоты и последствий в отображаемом риске. Таким образом, два риска с одинаковым уровнем, где у первого высокая частота и низкие последствия, а у второго – низкая частота и высокие последствия, никак не будут отличаться. Но, одномерное представление риска применимо в тех случаях, когда двумерное его представление невозможно, например, при выражении риска, являющегося интегральной оценкой нескольких рисков различных видов, имеющих одинаковую или различную размерность.

5.1.2 Двумерное представление уровня риска на графике риска

Двумерное представление риска на графике с координатами «частота-последствия» позволяет, кроме собственно уровня риска, отобразить информацию о характере сочетания частоты и последствий в данном риске. Такая информация является очень полезной, когда принимаются решения по обработке риска. Например, для «предсказуемого» события, которое случается с большой частотой, но имеет незначительный ущерб, могут быть разработаны мероприятия, направленные на снижение частоты его возникновения. Напротив, если событие случается крайне редко, но имеет значительные последствия, одним из решений может быть передача риска страховой компании.

При двумерном представлении риска масштаб осей координат может быть как линейным, так и логарифмическим. При линейном масштабе границы областей значений риска представляют собой гиперболы (рисунок 5.2а). В логарифмическом масштабе гиперболы спрямляются и отображаются в виде прямых линий с отрицательным тангенсом угла наклона (рисунок 5.2б).

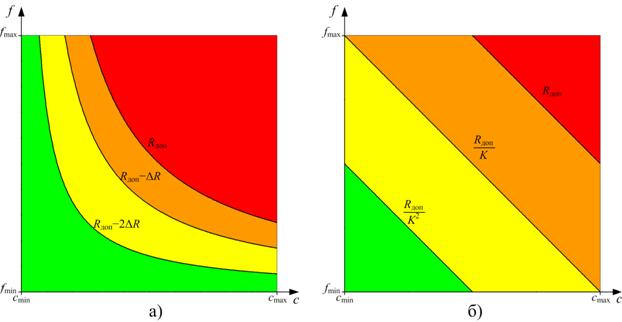
Рисунок 5.2 – Двумерное представление риска в системе координат «частота-последствия» с линейным (а) и логарифмическим масштабом

Очевидные преимущества логарифмического масштаба заключаются в большом диапазоне значений шкал частот, последствий и рисков, а также в отображении границ областей риска в виде прямых линий. Поэтому в настоящих МР далее при представлении риска в координатах «частота-последствия» будет применяться логарифмический масштаб.

Допущение 4 – Все параметры, относящиеся к определению уровня риска (частота, удельный размер последствий, уровень риска) представляются в логарифмической системе координат.

5.2 Общие требования к отображению поля ячеек на координатную плоскость

Поле ячеек матрицы рисков представляет собой прилегающие друг к другу ячейки прямоугольной формы, сгруппированные в структуру m строк x n столбцов. На рисунке 5.3 в качестве примера приведено поле ячеек размерностью 6 x 4, где a – высота, а b – ширина ячейки. В самом простом случае ячейка является квадратной a = b (хотя в графическом представлении матрицы для удобства ее просмотра предпочтительно использование прямоугольных ячеек, что будет рассмотрено ниже).

Рисунок 5.3 – Поле ячеек размерностью 6 x 4

Для корректного количественного представления уровня риска на поле ячеек необходимо, чтобы оно являлось частью координатной плоскости, имеющей (как это было принято выше) логарифмические координаты.

Первым требованием к отображению поля ячеек на координатную плоскость является обязательное присутствие в нем ячеек, принадлежащих ко всем (в нашем случае, четырем) областям значений уровня риска. На рисунке 5.4 показаны случаи отображения поля ячеек на координатную плоскость, где наклонными прямыми показаны границы областей значений рисков: 1 – корректное отображение (поле ячеек охватывает все области значений рисков); 2 – некорректное отображение (поле ячеек имеет приемлемые размеры, но неправильно расположено на плоскости); 3 – некорректное отображение (поле ячеек имеет недостаточные размеры).

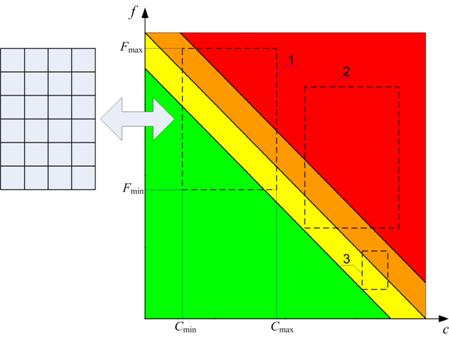
Рисунок 5.4 – Отображение поля ячеек на координатную плоскость

При отображении на координатную плоскость поле ячеек, кроме категорий рисков, также приобретает минимальные и максимальные значения частот и последствий (F_min, F_max, C_min, C_max).

При рассмотрении разделения координатной плоскости на области значений рисков можно сделать вывод о ее осевой симметрии. Осью симметрии является прямая, разделяющая области допустимого («желтый») и нежелательного («оранжевый») риска. Отсюда следует вывод о том, что при минимальных размерах поля ячеек, при которых оно охватывает все категории риска, центр поля ячеек должен быть расположен на этой оси симметрии. В таком случае части областей значений рисков, охватываемые полем ячеек, будут иметь попарно одинаковые площади (S₁ = S₄; S₂ = S₃, где индексы: 1 – область риска, не принимаемого в расчет (зеленый); 2 –область допустимого риска (желтый); 3 – область нежелательного риска (оранжевый); 4 – область недопустимого риска (красный)). Для того чтобы поле ячеек было центрально симметричным, в нем должно быть четное количество рядов и четное количество столбцов.

Допущение 5 – Поле ячеек матрицы рисков должно быть центрально симметрично, поэтому m и n должны быть четными.