Вероятность попадания случайной величины, подчиненной нормальному закону на заданный участок.

Известна. случайная величина Х, подчиненная нормальному закону с параметрами m_x и σ_х .

Требуется вычислить вероятность попадания случайной величины Х на участок от а до b.

Для вычисления этой вероятности воспользуемся формулой

P ( a ≤ X ≤ b) = F ( b ) – F ( a )

где F (x) – функция распределения случайной величины Х .

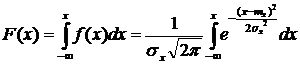
Сделаем замену переменных 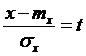; х = σ_хt + m_x ; dx = σ_x dt.

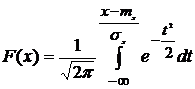, где .

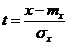Этот интеграл не выражается через элементарные функции, но его можно вычислить через специальные функции, дающие значения определенных интегралов от выражени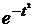й или 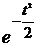, для которых составлены таблицы. Существует много разновидностей этих функций.

Часто применяется т.н. стандартная нормальная функция распределения вида

.

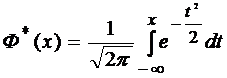Эта функция представляет собой функцию распределения для нормально распределенной случайной величины X с параметрами m_x = 0 , σ_х = 1.

Для стандартной нормальной функции распределения Ф^* ( х ) составлены таблицы.

0,5

0,5

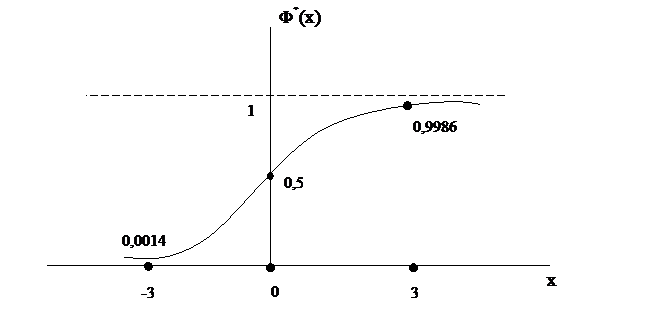
Как и всякая функция распределения, функции Ф^*(х) обладает свойствами:

1. Ф^*(- ∞) = 0;

2. Ф^*(+ ∞) = 1;

3. Ф^*( х ) – неубывающая функция .

4. Из симметричности f ( x ) нормального распределения с параметрами m_x = 0

и σ = 1 относительно начала координат следует:

Ф^* (-x ) = 1 – Ф^* ( х ) .

Выразим функцию распределения случайной величины Х с параметрами m_x и σ_х через стандартную нормальную функцию распределения Ф^* (х).

Т.к. ,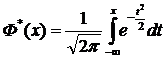

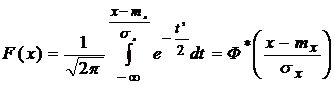
Величина 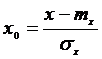- называется нормированной случайной величиной, для которой M [x₀] = 0 , а D[x₀] = 1.

Вероятность попадания случайной величины Х на участок от а до b :

P ( a ≤ X <b) = F ( b ) – F ( a ) = .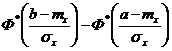

На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m_x

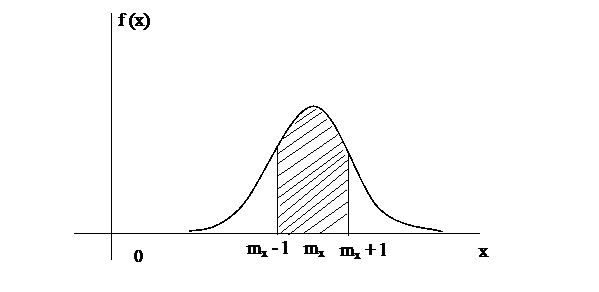
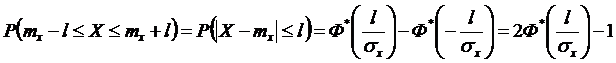
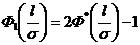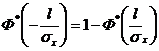т.к. , то ,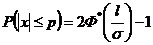

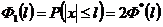
Связь квадратной нормальной функции распределения, функции Лапласа и интеграла вероятности.

=

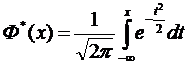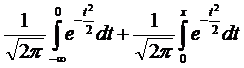
так как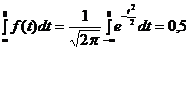

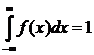
Следовательно, Ф^* (х) = 0,5 + Ф ( х )

Ф₁ ( х ) = 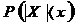= 2 Ф ( х )

Ф^* (х) = 0,5 +0,5 Ф₁ ( х ) = 0,5 ( 1 + Ф₁ (х))

Если пользоваться таблицей Ф^* ( х ), то .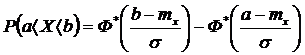

Если пользоваться таблицей Ф₁ ( х ) то .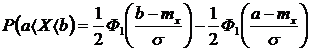

Ф₁ ( х ) = 2 Ф^*(х) – 1.

Правило трех сигм.

Отложим от m_x отрезки длиной σ и вычислим вероятность попадания случайной величины в каждый из них.

Т.о. случайная величина с вероятностью 0,9973 находится в интеграле [m_x - 3σ_x, m_x + 3σ_x].

Это значит, что для нормально распределенной случайной величины всё рассеивание ( с точностью до долей процента ) укладывается на участке m_x ± 3σ_x

Иначе, вероятность того, что отклонение случайной величины от математического ожидания превысит 3σ, практически равна 0, т.е. это событие считается практически невозможным событием ( т.н. правило трёх сигм).

Т.о. зная σ и m_x, можно ориентировочно указать интервал возможных значений случайной величины.

Из правила трёх сигм вытекает также ориентировочный способ определения σ :

берут максимальное практически возможное отклонение от среднего и делят его на 3.

Кроме нормального распределения и равномерного широко используют другие типы распределений случайных величин.