О мощности множеств действительных чисел
 В п. 2.2 утверждалось, что множества точек отрезка [0, 1] и отрезка [a, b] равномощны. Доказать это нетрудно: взаимно однозначное соответствие [0, 1]
В п. 2.2 утверждалось, что множества точек отрезка [0, 1] и отрезка [a, b] равномощны. Доказать это нетрудно: взаимно однозначное соответствие [0, 1] 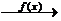 [a, b] может быть установлено функцией Y = (b - a) • X + a. Если X = 0, то Y = a; если X = 1, то Y = b, откуда, если
[a, b] может быть установлено функцией Y = (b - a) • X + a. Если X = 0, то Y = a; если X = 1, то Y = b, откуда, если
0≤ X ≤ 1, то a ≤ Y ≤ b (рис. 10).
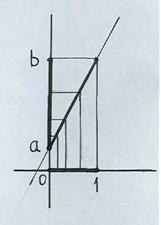
Рис. 10
Тем самым отрезки разной длины равномощны (по-другому, эквивалентны). На рис. 11 графическая иллюстрация этого факта. Можно показать также равномощность отрезка и интервала, непосредственно указав взаимно однозначное соответствие (рис. 12).

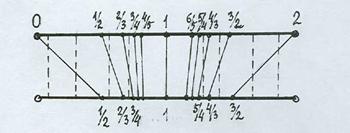
Рис. 11 Рис. 12
На отрезке [0, 1] каждому числу вида (n-1)/n: 0, 1/2, 2/3, 3/4, 4/5 и т.д. ставится в соответствие следующее число этой последовательности. На отрезке [1, 2] соответствие симметрично: последовательность имеет вид (n+1)/n: 2, 3/2, 4/3, 5/4... Всем остальным числам отрезка [0, 2] ставятся в соответствие они сами. Концы интервала не соответствуют при этом ни одной точке отрезка.
Однако можно воспользоваться более общим утверждением (равномощность множеств А и В обозначается А ~ В).
Теорема. Пусть А и В - два множества, А¢, В¢ - их подмножества: А¢ Í А, В¢ Í В. Пусть каждое из множеств А, В эквивалентно подмножеству другого: А ~ В¢, А¢ ~ В. Тогда А ~ В, т.е. множества эквивалентны.
Для любого отрезка и любого интервала отсюда следует их эквивалентность (рис. 13). 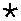
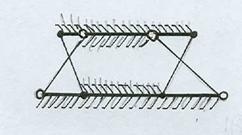
Рис. 13
Рис. 14 иллюстрирует равномощность интервала и множества точек всей прямой.
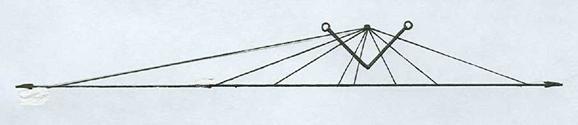
Рис. 14
Приложение 3
Двоичный 5-мерный куб
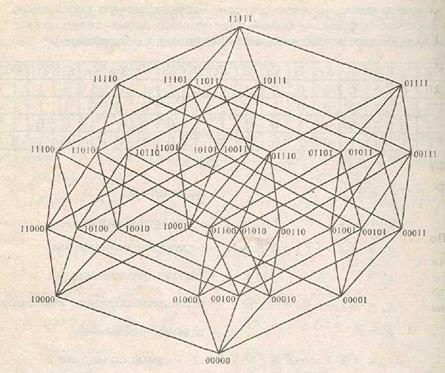
Рис. 15
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Составьте логическую схему базы знаний по теме юниты:
2. Решить задачи 1–10.
Для выполнения работы необходимо определить и записать в таблицу К1 значения переменных а1- а42(нули и единицы), исходя из следующих параметров:
F – первая буква фамилии,
N – первая буква имени, Впишите свои параметры в табличку:
| F = | N = | S = |
S – число букв в фамилии.
(Пример. Евгений Онегин: F = О, N = Е, S = 6.)
Таблица К1
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 | а10 | а11 | а12 | а13 | а14 |
| а15 | а16 | а17 | а18 | а19 | а20 | а21 | а22 | а23 | а24 | а25 | а26 | а27 | а28 |
| а29 | а30 | а31 | а32 | а33 | а34 | а35 | а36 | а37 | а38 | а39 | а40 | а41 | а42 |
Алгоритм заполнения таблицы К1. Значения а1 - а42выбираются из внутреннего кольца круговой диаграммы (рис. 1), разделенной на 28 секторов, которые обозначены буквами от А до Я (во внешнем кольце) и одновременно числами от 1 до 28 (в среднем кольце). Буква Ё считается совпадающей с Е; Й и Ы – совпадающими с И.
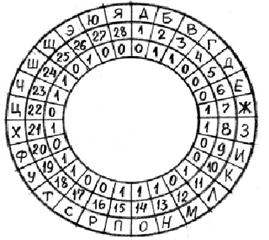
Рис. 1
Выбор значений а1 - а42производится по следующему правилу:
а1 - а14– 14 чисел (нулей и единиц) подряд по часовой стрелке, начиная с позиции F;
а15- а28– 14 чисел подряд по часовой стрелке, начиная с позиции N;
а29- а42– 14 чисел подряд против часовой стрелки, начиная с позиции S;
Пример заполнения таблицы К1 для F = О, N = Е, S = 6:
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 | а10 | а11 | а12 | а13 | а14 |
| а15 | а16 | а17 | а18 | а19 | а20 | а21 | а22 | а23 | а24 | а25 | а26 | а27 | а28 |
| а29 | а30 | а31 | а32 | а33 | а34 | а35 | а36 | а37 | а38 | а39 | а40 | а41 | а42 |
В каждой из нижеследующих задач (1–10) определенным образом осуществляется выбор переменных 0, 1 из заполненной таблицы К1; из этих цифр составляются многозначные двоичные числа, которые затем используются в качестве параметров (в виде двоичных чисел или переводятся в десятичную систему). Правильное выполнение этих арифметических операций наряду с правильным исполнением инструкции в условии задачи, является неотъемлемой частью решения. К задачам 1, 4, 8, 9 приведены примеры решения.
Задача 1.Перевести в десятичную систему четырехзначное двоичное число А2= а1а2а3 а4и трехзначное двоичное число В2= а5а6а7. Вычислить число С10= (A + 5) · (23 – А) + В. Перевести число С10в двоичную систему. В полученном числе С2зачеркнуть две последние цифры и перевести результат – двоичное число D2– в десятичную систему.
Пример.Возьмем данные из примера заполнения табл. К1.
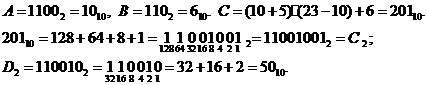
Задача 2.Двоичные числа a = a11a12, b = a13a14,c = a15 a16a17 a18a19, d = a20 a21 (a, b, d–двузначные,c – пятизначное) перевести в десятичную систему. Изобразить на числовой прямой отрезок K = [a, a+b+14] и интервал L= (c, c+d+18), а также множества K∩ L, KÈ L, K \ L, L \ K.
Перевести в десятичную систему пятизначные двоичные числа E= a22a23a24a25a26и
F = a27 a28 a29 a30 a31. Заполнить таблицу К2, ставя на пересечении строки, соответствующей точке EиF, и столбца, соответствующего множеству K, L, K∩ L, KÈ L, K \ L, L \ K, знак + или–
в зависимости от того, принадлежит ли точка этому множеству.
Таблица К2
| K | L | K ∩ L | K È L | K \ L | L \ K | |
| E | ||||||
| F |
Задача 3.Перевести в десятичную систему двоичные числа А = а21а22а23, В = а24а25а26,
C = а27а28, D = а29 а30а31а32, E = а33а34а35а36, F = а37а38а39а40, K = а41а42. Решить задачу с номером (K+1) из четырех нижеследующих (числа A, B, C, D, E, F определяют содержащиеся в них параметры).
1. Из 100 школьников (50 + А) играют в баскетбол, (20 + В) - в волейбол, (35 + С) не играют в эти игры. Сколько человек играют и в баскетбол, и в волейбол? Сколько процентов школьников, играющих в баскетбол, играют в обе игры?
2. Из 100 студентов (53 + А) любят слушать музыку, (23 + В) занимаются спортом, причем
(5 + D) студентов занимаются спортом и любят слушать музыку. Сколько человек не увлекаются ни спортом, ни музыкой? На сколько процентов это число меньше числа любителей музыки?
3. Среди 100 туристов одним английским языком владеют (35 + D), английским и немецким -
Е человек; не владеют ни английским, ни немецким – F туристов. Сколько человек владеют немецким, сколько владеют только немецким? Сколько процентов туристов, владеющих немецким, не владеют английским?
4. Опрос 100 школьников показал, что (50 + D) человек умеют играть в шахматы, Е – и в шахматы, и в шашки, (20 + F) – только в шашки. Сколько школьников не играют ни в одну из этих игр? Сколько человек умеют играть в шашки? Сколько процентов школьников, играющих в шашки, не умеют играть в шахматы?
Задача 4.Перевести в десятичную систему двоичное число d = a33 a34 a35.
Вычислить десятичные числа ti = ai+35 + 2 (i = 1, 2,..., 7):
t1 = a36 + 2, t2 = a37 + 2,..., t7 = a42 + 2.
Множество М определяется порождающей процедурой:
(1) d Î M;
(2) если b Î M, то b + 3Î M;
(3) если b Î M, то3b Î M.
Вычислить результат применения к исходному значению d последовательности операций (t1), (t2), (t3), (t4), (t5), (t6), (t7).
Пример. Значения ti могут равняться либо 2, либо 3. Пусть d = 5; ti = 3, 2, 2, 2, 3, 2, 3. Тогда последовательно получаем: b = 15, 18, 21, 24, 72, 75, 225.
Задача 5.Перевести в десятичную систему следующие двоичные числа:
C = a35 a36 a37, D = a38 a39a40, E = a41 a42. Вычислить значения А = С – 6, В = D + 2.
Отрезок [A, B] отображается функцией f(x) = (x + E)2 в множество L. Найти множество (промежуток) L. Является ли отображение [A, B] 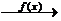 L взаимно однозначным?
L взаимно однозначным?
 Задача 6.Перевести в десятичную систему следующие двоичные числа:
Задача 6.Перевести в десятичную систему следующие двоичные числа:
C = a29 a30 a31, D = a32 a33a34. Вычислить А = С + 1, В = D – 6.
Определить номер, который получают при нумерации целочисленных точек плоской решетки, изображенной на рис. 2.2 (стр. 20), точки с координатами (А, В), (В, А), (-А, -В). 
Задача 7. Перевести в десятичную систему следующие двоичные числа:
b = a1 a2 a3, X = a4 a5a6 a7, Y = a8 a9 a10 a11, Z = a12 a13 a14 a15.
Для чисел X, Y, Z вычислить значения суперпозиции с номером b:
0) min (X, max (Y, Z));
1) min (max (X, Y), Z);
2) max (min (X, Y), Z);
3) max (X, min (Y, Z));
4) max (min (X, Z), Y);
5) min (Y, max (X, Z));
6) min (max (Y, Z), X);
7) max (Z, min (X, Y)).
Задача 8. Схема 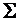 из функциональных элементов имеет структуру, изображенную на рис. 2. Элементы реализуют двуместные функции, которые определяются двузначными двоичными числами, образованными из знаков
из функциональных элементов имеет структуру, изображенную на рис. 2. Элементы реализуют двуместные функции, которые определяются двузначными двоичными числами, образованными из знаков
а5 - а16: S1 = а5 а6 ; S2 = а7 а8 ; S3 = а9 а10 ; S4 = а11 а12 ; S5 = а13 а14 ; S6 = а15 а16 .
00 + (сложение); 01 – (вычитание);
10 ·(умножение); 11 / (деление).
1. Подставив на место элементов S1–S6конкретные арифметические операции, составить формулу для функции W(X, Y, Z), реализуемой схемой 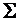 .
.

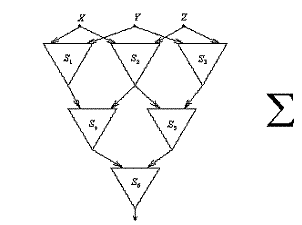
Рис. 2
2. Вычислить значение функции при значениях аргументов
X = 2 + a17 a18 a19 ; Y = 3 + a20 a21 a22 ; Z = 4 + a23 a24 a25 .
Пример. Пусть а5 - а16 = 110010100111
S1– 11 / На выходе элемента S1 : Х / Y
S2– 00 + На выходе элемента S2: X + Z
S3– 10 ·На выходе элемента S3 : Y · Z
S4– 10 ·На выходе элемента S4 : (X / Y) ·(X + Z)
S5– 01 – На выходе элемента S5 : (X + Z ) – Y · Z
S6– 11 / На выходе элемента S6 , т.е. на выходе схемы:
(X / Y) · (X + Z) / ((X + Z) – Y · Z).
Если Х = 5, Y = 9, Z = 6, то W = 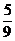 • 11 / (11 – 54) =
• 11 / (11 – 54) = 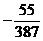 .
.
Задача 9.Перевести в десятичную систему следующие двоичные числа:
А = a1 a2, В = a3 a4, C = a5 a6 , D = a7 a8 , E = a9 a10;
X = 4 + a11 a12 a13 , Y = 5 + a14 a15 a16 , Z = 6 + a17a18 a19 .
В формуле W = [(X A Y) B (Y C Z)] D (X E Z) заменить двузначные двоичные символы A, B, C, D, E на знаки арифметических операций:
00 + (сложение); 01 – (вычитание);
10 ·(умножение); 11 / (деление).
Построить схему 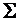 , реализующую эту формулу. Вычислить значение W(X, Y, Z) при заданных значениях X, Y, Z.
, реализующую эту формулу. Вычислить значение W(X, Y, Z) при заданных значениях X, Y, Z.
Пример. Пусть А = 1 0, В = 0 1, C = 1 1, D = 1 1, E = 0 0 ; X = 7, Y = 8, Z = 12.
Тогда формула приобретает вид W = [(X · Y) – (Y / Z)] / (X + Z). Подстановка значений X, Y, Z дает W = [(7· 8) – (8 / 12)] / (7 + 12) = (56 – 2/3) / 19 = 166/57.
Задача 10.Перевести в десятичную систему двоичное число R = a26 a27 a28.
Является ли бинарное отношение с номером R между числами, точками, геометрическими фигурами транзитивным, симметричным, антисимметричным?
0) Прямая l1 пересекается с прямой l2.
1) Квадрат K1 на плоскости находится внутри квадрата K2.
2) Точка А на оси ОХ находится между началом координат и точкой В.
3) Точка земной поверхности А находится на той же высоте над уровнем моря, что и точка В.
4) Целое число А делится без остатка на целое число В.
5) Целое число А имеет общий множитель, не равный 1, с числом В.
6) Точка А на окружности диаметрально противоположна точке В.
7) Дуга окружности между точками А и В составляет 90º.
ТРЕНИНГ УМЕНИЙ
Пример выполнения упражнения тренинга на умение № 1
Задание
Перевести в двоичную систему десятичные числа: 82, 173.
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Использовать шкалу сте-пеней основания двоичной системы – числа 2 | 0 1 2 3 4 5 6 7 8 ... 1 2 4 8 16 32 64 128 256 ... | |
| Представить заданное чис-ло в виде суммы элемен-тов шкалы, последователь-но выделяя максимально возможное слагаемое | 82 = 64 + 18 = 64 + 16 + 2 173 = 128 + 45 = 128 + 32 + 13 = = 128 + 32 + 8 + 5 = 128 + 32 + 8 + 4 + 1 | |
| Выделить на шкале слага-емые, участвующие в раз-ложении: им соответст-вует цифра 1 в двоичном представлении; отсутст-вующим – цифра 0 | 6 5 4 3 2 1 0 64 32 16 8 4 21 1 0 1 0 0 1 0 8210 = 10100102 7 6 5 4 3 2 1 0 128 64 3216 8 42 1 1 0 1 0 1 1 0 1 17310 = 101011012 |
Решите самостоятельно следующие задачи:
Перевести в двоичную систему десятичные числа: 21, 56, 74, 90, 101, 123.
Пример выполнения упражнения тренинга на умение № 2
Задание
Перевести в десятичную систему двоичное число: 1101001.
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Использовать шкалу сте-пеней основания двоич-ной системы числа 2 | 0 1 2 3 4 5 6 7 8 ... 1 2 4 8 16 32 64 128 256 ... | |
| Сопоставить знакам 1 в двоичном представлении заданного числа элемен-ты шкалы | 1 1 0 1 0 0 1 6 5 4 3 2 1 0 64 3216 8 4 2 1 | |
| Сложить выделенные числа – степени числа 2 | 11010012 = 64 + 32 + 8 + 1 = 10510 |
Решите самостоятельно следующие задачи:
Перевести в десятичную систему двоичные числа: 10010, 110101, 101001, 1000110, 1110100, 1011001.
Пример выполнения упражнения тренинга на умение № 3
Задание
А и В – множества действительных чисел: А = (-2, 4), В = [0, 7].
Найти и показать на числовой прямой множества А Ç В, A È В, А \ В, А \ В, 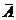 .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Изобразить множества А и В на числовой прямой | А = (-2, 4) - интервал, концы промежутка не принадлежат множеству В = [0, 7] - отрезок, концы промежутка принадлежат множеству 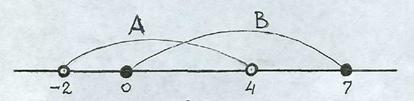 | |
| А Ç В – пересечение множеств А и В | А Ç В - полуинтервал [0, 4)  | |
| A È В - объединение множеств А и В | A È В - полуинтервал (-2, 7] 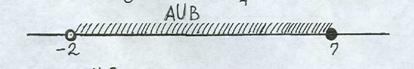 | |
| A \ В - разность множеств А и В | A \ В - интервал (-2, 0): точка 0 не входит в интервал, поскольку она принадлежит множеству В.  -2 0 -2 0 | |
| B \ A - разность множеств А и В | В \ А - отрезок [4, 7]: точка 4 входит в отрезок, поскольку она не принадлежит множеству А.  | |
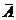 - дополнение множества А - дополнение множества А | 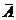 - объединение двух бесконечных промежутков (-¥, -2] È [4, +¥): концы интервала не принадлежат ему и поэтому входят в дополнение - объединение двух бесконечных промежутков (-¥, -2] È [4, +¥): концы интервала не принадлежат ему и поэтому входят в дополнение  |
Решите самостоятельно следующие задачи:
Найти и показать на числовой прямой множества А Ç В, A È В, А \ В, А \ В, 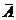 ,
, 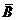 для множеств:
для множеств:
1) А = [-2, 0], В = (-6, 1];
2) А = (0, 4), В = [-5, 1];
3) А = [-2, 5], В = [0, 3];
4) А = [-6, 4), В = [0, 7];
5) А = (-2, 4), В = (0, 7).
Пример выполнения упражнения тренинга на умение № 4
Задание
Определить, какую функцию двух переменных W(X, Y) реализует схема, изображенная
на рис. 3.
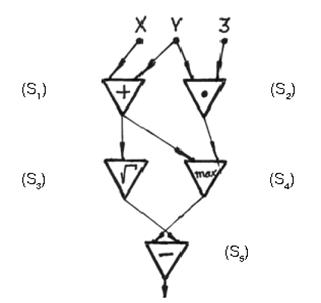
Рис. 3
Решение
| № п/п | Алгоритм | Конкретное соответствие задания заданному алгоритму |
| Пронумеровать эле-менты и сопоставить им реализуемые ими одноместные и дву-местные операции | Нумерация элементов – на рис. 3 S1 = X + Y; S2 = Y • 3; S3 = 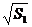 ; S4 = max (S1 , S2); S5 = S4 – S3. Для некоммутативной операции вычитания значение на выходе элемента S4 подается на первый (левый) вход элемента S5; вычитаемое S3 – подается на второй (правый) вход S5 ; S4 = max (S1 , S2); S5 = S4 – S3. Для некоммутативной операции вычитания значение на выходе элемента S4 подается на первый (левый) вход элемента S5; вычитаемое S3 – подается на второй (правый) вход S5 | |
| Записать формулами суперпозиции проме-жуточных данных, последовательно вы-полняя соответст-вующие подстановки | S3 = 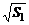 = = 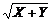 ; S4 = max (S1 , S2) = max (X + Y, Y • 3); W = S5 = S4 – S3 = max (X + Y, Y • 3) – ; S4 = max (S1 , S2) = max (X + Y, Y • 3); W = S5 = S4 – S3 = max (X + Y, Y • 3) – 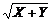 |
Решите самостоятельно следующие задачи:
1. Определить, какую функцию двух переменных W(X, Y) реализует схема, изображенная на рис. 4, а, б, в.
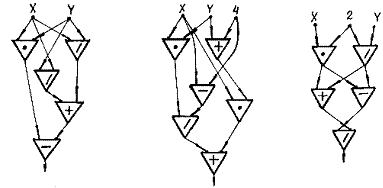
а б в
Рис. 4
2. Определить, какую функцию трёх переменных W(X, Y, Z) реализует схема, изображенная на рис. 5, а, б.
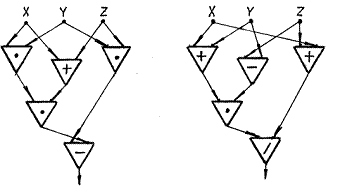
а б
Рис. 5
Пример выполнения упражнения тренинга на умение № 5
Задание
Определить порядка действий при вычислении значения суперпозиции элементарных функций и простых многоместных функций. Построить схемы из функциональных элементов, реализующей функцию
Z = 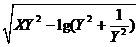 .
.
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Определить состав пере-менных и констант в фор-муле, которая задает функ-цию | Переменные X, Y; константа 1. | |
| Определить внешнюю опе-рацию (функцию) и основ-ные подформулы | Z = 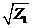 , где , где 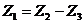 Z2 = XY2; Z3 = lg Z4; Z4 = Y2 + Z2 = XY2; Z3 = lg Z4; Z4 = Y2 + 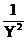 | |
| Определить, какие из функ-ций, составляющих супер-позицию, являются одно-местными, а какие – двуместными | Оперaции lg (логарифмирование) и 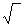 (извлечение квадратного корня) – одноместные; арифметические операции +, –, ·, / – двуместные (извлечение квадратного корня) – одноместные; арифметические операции +, –, ·, / – двуместные | |
| Составить иерархическую схему последовательности действий | Z = 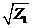 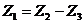 Z2 = X · Z5 Z3 = lg Z4 Z4 = Z5 + Z6 Z5 = Y2 Z6 = Z2 = X · Z5 Z3 = lg Z4 Z4 = Z5 + Z6 Z5 = Y2 Z6 = 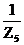 | |
| Построить схему из функциональных элементов в соответствии с иерархической схемой вычисления а) определить совокупность используемых элементов с одним и двумя входами; б) выделить подформулы, имеющие в суперпозиции больше одного вхождения; в) осуществить необходимое соединение элементов | 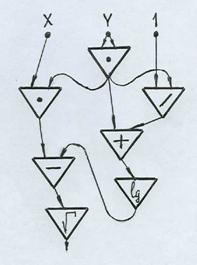 |
Решите самостоятельно следующие задачи:
Построить схемы из функциональных элементов, реализующие функции:
1. 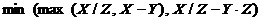
2. 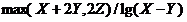
3. 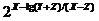
4. 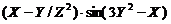
5. 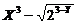
6. 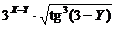
Пример выполнения упражнения тренинга на умение № 6
Задание
Используя диаграмму Венна, решить следующую задачу. В экспресс-опросе 200 жителей выяснено, что 80 человек сегодня воспользовались метрополитеном и автобусом,
30 - метрополитеном и троллейбусом, 10 - автобусом и троллейбусом; 70 – только одним видом транспорта; 50 – сегодня не пользовались общественным транспортом. Определить число жителей, использовавших все три вида транспорта.
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Представить соотношения между множествами, заданными в условии диаграммой Венна : универсальное множество U и его подмножества в общем положении, образующие разбиение {Bi} множества U | U – универсальное множество участников опроса. М – подмножество пассажиров метрополитена, А – подмножество пассажиров автобусов, Т – подмножество пассажиров троллейбусов. M = B1 È B2 È B4 È B5; A = B2 È B3 È B 5 È B6. T = B4 È B5 È B6 È B7. 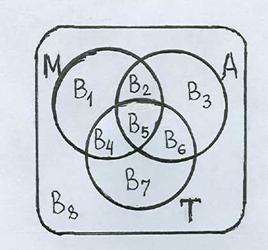 |
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Обозначить заданную в условии численность подмножеств, составленных из элементов разбиения множества U | ½U½= 200. ½B8½= 50. ½B2 È B5½= 80. ½B4 È B5½= 30. ½B5 È B6½= 10. ½B1 È B3 È B7½= 70. Требуется найти ½B5½. | |
| Составить численные соотношения между заданными множествами | Общее число пассажиров: ½MÈAÈT½= ½B1½+½B2½+½B3½+½B4½+½B5½+½B6½+½B7½= = ½U½–½B8½= 200 – 50 = 150. (1) Поскольку попарные пересечения блоков разбиения пусты, то: ½B2 È B5½ = ½B2½+½B5½ = 80. ½B4 È B5½ = ½B4½+½B5½ = 30. ½B5 È B6½ = ½B5½+½B6½ = 10. | |
| Из полученных соотноше-ний найти требуемое число | Почленное сложение трех предыдущих равенств дает: ½B2½+½B4½+½B6½+ 3·½B5½= 80 + 30 + 10 = 120. (2) Число использовавших только один вид транспорта, равно: ½B1 È B3 È B7½= ½B1½+½B3½+½B7½ = 70. Составляем соотношение: 150 = 70 + ½B2½+½B4½+½B6½+½B5½ Þ Þ ½B2½+½B4½+½B6½+½B5½ = 150 – 70 = 80. (3) Почленно вычитаем из равенства (2) равенство (3): 2·½B5½= 120 – 80 = 40 Þ ½B5½ = 20. |
Решите самостоятельно следующие задачи:
Проверить, истинны ли соотношения между множествами:
1. А \ (В È С) = А \ В \ С
2. (А \ В) È (В \ А) = (А È В) \ (А ∩ В)
3. А \ (В ∩ С) = (А \ В) È (А \ С)
4. А \ (А \ В) = (А ∩ В)
5. А \ (В \ А) = А \ В
ГЛОССАРИЙ
| № п/п | Новое понятие | Содержание |
| Множество | совокупность элементов, набор каких-либо предметов (объектов); обозначение A ={x: p(x)} - A есть множество элементов х, удовлетворяющих условию p(x) | |
| Характеристическое свойство элементов множества А | свойство, которым обладают все элементы множества А и не обладает ни один из элементов, не принадлежащих А | |
| Подмножество | множество Н, каждый элемент которого принадлежит также множеству М, называется подмножествоммножества М | |
| Пересечение множеств | множество А ∩ В, состоящее из элементов, принадлежащих множеству А и множеству В одновременно | |
| Объединение множеств | множество А È В, состоящее из всех элементов, которые принадлежат множеству А или множеству В | |
| Разность множеств | множество А \ В, состоящее из тех элементов множества А, которые не принадлежат множеству В | |
| Симметрическая разность множеств | множество А Δ В, состоящее из всех элементов, которые принадлежат ровно одному из множеств А и В | |
| Дополнение множества | множество 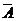 , состоящее из всех элементов универсального множества, не входящих в множество А , состоящее из всех элементов универсального множества, не входящих в множество А | |
| Разбиение множества | система {Bα} непустых подмножеств множества A, что все попарные пересечения – пусты (Bi ∩ Bj = Æ, если i ≠ j, а их объединение ÈBα равно A. Сами Bα называются классами, или блоками разбиения. | |
| Декартово (прямое) произведение множеств | 1) для двух множеств: произведение A ´ B - множество всех пар (a, b), где a Î A, b Î B; 2) для n множеств: произведение A1 ´ A2 ´...´ An – множество всех векторов (a1, a2,…,an), где ai Î Ai (т.е. a1Î A1, a2 Î A2,..., an Î An); если все Ai одинаковы и равны A, то произведение A ´ A ´….´ A обозначается An и n раз называется n-й степенью множества A | |
| Соответствие между множествами | соответствие A → B: всем или некоторым элементам множества А сопоставлены каким-нибудь способом один или несколько элементов множества В | |
| Образ элемента а при соответствии А→В | множество всех элементов b Î B, соответствующих элементу а Î А | |
| Прообраз элемента b при соответствии А→В | множество всех элементов a Î A, которым соответствует элемент b Î B | |
| Однозначное (функциональное) соответствие A → B, или отображение множества A в множество B | соответствие, при котором каждому элементу a Î A поставлен в соответствие единственный элемент b Î B | |
| Взаимно-однозначное соответствие (взаимно-однозначное отображение) множеств | правило, при котором каждому элементу A поставлен в соответствие один элемент множества B, и при этом соответствии каждый элемент B соответствует одному и только одному элементу А | |
| Эквивалентные множества | множества, между которыми можно установить взаимно однозначное соответствие |
| Счетное множество | множество, эквивалентное множеству натуральных чисел | |
| Интервал (открытый промежуток) | множество чисел A = {x: a < x < b}, расположенных в промежутке между числами a и b; обозначение (a, b). Концы промежутка не принадлежат интервалу | |
| Отрезок (замкнутый промежуток) | множество чисел B = {x: a ≤ x ≤ b} обозначается [a, b]. Концы промежутка принадлежат интервалу | |
| Окрестность точки | любой интервал, содержащий эту точку | |
| Суперпозиция функций | функция, полученная из n-местной функции f(x1, x2,.., xn) и системы n функций g1, g2,..., gn некоторой подстановкой функций g1, g2,..., gn во внешнюю функцию f вместо переменных и переименованиями переменных | |
| Формула | выражение, описывающее суперпозицию и содержащее функциональные знаки, символы независимых переменных (аргументов) и констант (параметров) | |
| Характеристическая функция множества | пусть В = {0, 1} – множество из двух чисел. Для подмножества М универсального множества U (M Í U) – отображение χM: U → B, ставящее в соответствие элементам множества M единицу, а элементам дополнения 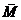 – ноль – ноль | |
| Булеан В(Е) | множество всех подмножеств множества Е | |
| Схема из функциональных элементов | сеть, элементам которой приписаны (сопоставлены) функции, так что элементу S с k входами соответствует k-местная функция f(x1, x2,..., xk) | |
| Бинарная алгебраическая операция φ(a, b), или a φ b на множестве М | паре элементов a, b множества М сопоставляется элемент того же или другого множества | |
| Множество, замкнутое относительно операцииφ | применение операции φ не выводит за пределы множества М, т.е. всякий результат операции φ над элементами множества М также принадлежит М | |
| Алгебра | система А = (L; Ω), состоящая из множества L и набора операций Ω = {φ1, φ2,..., φk}, действующих на множестве L. Множество L называется носителем, а система операций Ω – сигнатурой алгебры А | |
| Алгебра множеств (алгебра Кантора) | система (В(U), È, ∩, ‾‾) на булеане В(U) с операциями объединения, пересечения и дополнения | |
| Ассоциативная бинарная операция | операция φ, обладающая сочетат |
