Линия положения - это касательная к навигационной изолинии в счислимой точке.

Уравнение (2.4), с учетом формул п.1.1, может быть переписано в виде:

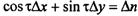
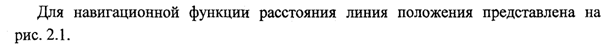
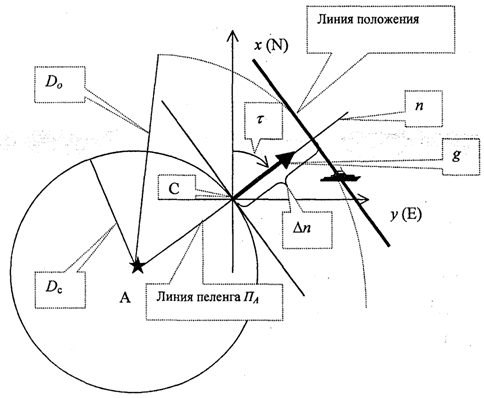
Рис. 2.1. Линия положения

2.2. Аналитический вариант расчета координат места судна по двум линиям положения

Для определения места судна достаточно измерить два навигационных параметра, т.к. поверхность, на которой ищутся обсервованные координаты, -двухмерная (положение точки определяется двумя координатами).

Алгоритм расчета таков:

а) в момент времени t измеряются два навигационных параметра Uoi и Uo2,

б) на этот же момент времени снимаются счислимые координаты Хс, ус и на них рассчитываются счислимые навигационные параметры Uci и Uc2,

в) для счислимых координат рассчитываются коэффициенты линий положения Дц, т.е. частные производные по навигационным параметрам от навигационных функций;

г) правые части уравнений линий положения рассчитываются по формулам: au]

=U,l-Ucl,^U2=^o2-Vc2;

д) составляется система двух уравнений линий положения, которая может быть переписана в матричном виде:

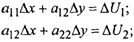
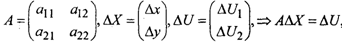
где А - матрица коэффициентов линий положения, АХ- вектор неизвестных, AU-вектор измерений (вектор свободных членов);

е) решение системы уравнений линий положения (2.6) запишется в виде:

•• ^/

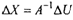
ж) если обозначить вектор счислимых координат как Хс, а вектор обсервованных координат как Ху, то можно записать:

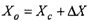
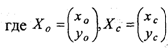
Так как вследствие линеаризации навигационных функций появляются методические погрешности, то для их компенсации используется итерационная процедура (метод последовательных приближений), т.е. обсервованные координаты принимаются за новые счислимые (Хо=Хс}, и вычисления продолжаются согласно указаниям пп. б), а заканчиваются тогда, когда длина вектора АХ не будет меньше наперед заданной величины е. Для навигационных задач это составляет обычно 2-3 итерации.

Расчет координат при избыточном числе измерений навигационных параметров

Равноточные измерения

Число навигационных измерений при определении места судна очень существенно. Если измеряются два навигационных параметра и определяются две координаты, то говорят, что в задаче отсутствует избыточность, т.е. система уравнений (2.6), как правило, совместна.

Отсутствие избыточности измерений приводит к неконтролируемому влиянию различных видов погрешностей на результат, особенно опасны грубые промахи и систематические погрешности.

Для получения более надежной обсервации применяют избыточные навигационные измерения.

Пусть для определения координат измерены три навигационных параметра (п = 3), а определить нужно две координаты (k = 2). В этой ситуации избыточность r= n-k=1.

Первоначально систему уравнений линий положения в матричном виде запишем так же, как систему уравнений (2.6):

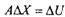
однако матрицы будут иметь вид:

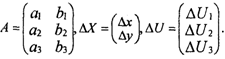
В данной системе количество неизвестных k меньше, чем количество уравнений п. Решение любых двух уравнений дает положение одной из вершин треугольника. Это означает, что подстановка этого решения в третье уравнение, не обратит его в тождеств \ Такая система называется несовместной, т.е. решение пары уравнений не совместно с третьим. Для получения согласованного решения системы необходимо ввести дополнительные условия. Если предположить, что систе­

матические погрешности в изме­рениях отсутствуют, т.е. они определены и исключены специ­альными приемами измерений, то все остальные погрешности изме­рений можно считать случайными. Известно, что центром группиро­вания случайных величин явля­ется их математическое ожидание или его оценка - среднее зна­чение, которое наиболее близко к истинному значению и имеет ми­нимальную дисперсию. Очевидно, что и в данном случае необходимо

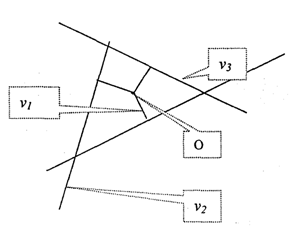
Рис. 2.2. К выводу формулы решения системы уравнений (2.7)

найти некоторое среднее из трех точек, которое будет иметь статус оценки математического ожидания множества, состоящего из трех измерений. Ясно, что эта точка должна быть в фигуре погрешностей, а не вне ее. Несогласованность измерений возникает из-за погрешностей, которые называют невязками системы уравнений.

Теперь вместо системы (2.9), с учетом невязок, более корректно следует записать следующее матричное уравнение (система уравнений поправок):

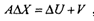
где V- вектор невязок (погрешностей), который имеет вид:

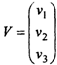
Если принять, что для получения согласованного решения линии положения необходимо сдвинуть внутрь фигуры погрешностей на некоторые величины v/, v^ и уз соответственно (рис. 2.2), то математическое условие поиска оптимального согласованного решения относительно этого среднего значения (точка О) определится в соответствии с формулой (2.11), т.е. минимальной длиной вектора V:

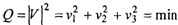
здесь величины v\, v-г. и уз, выраженные в единицах измерений, называются невяз­

ками, поправками или погрешностями измерений в за­висимости от при­даваемого им знака. Выражение (2.11) определяет усло­вие решения сис­темы (2.10), а от­сюда и название рассматриваемого метода — метод наименьших квад­ратов.

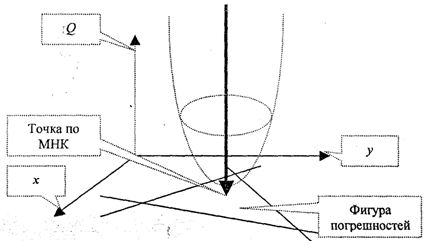
Рис. 2.3. Геометрическая интерпретация МНК

Из формулы (2.10) запишем выражение относительно вектора невязок:

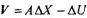
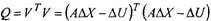
Взяв производную от выражения (2.12) по вектору неизвестных и приравняв ее к нулю, находим формулу для решения системы (2.10):

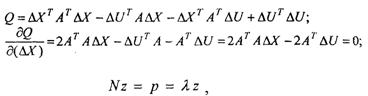
Система (2.13) называется системой нормальных уравнений. Теперь можно записать решение:

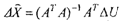
Знак «^л» над вектором искомых величин свидетельствует о том, что решение получено с применением критерия оптимальности Q, Рис. 2.3 поясняет решение по МНК.

После получения решения, согласно выражению (2.14) относительно счислимой точки в локальной системе координат, используется формула (2.8), а затем вьшолняется итерационная процедура. Точка, положение которой определяется вектором Хо, называется ввроятнвйшвй точкой.

Неравноточные измерения

В п. 2.3.1 никак не рассматривался вид погрешности измеряемых навигационных параметров, они считались равноточными, т.е. имеющими одинаковые средние квадратические погрешности т.

В общем случае измерения навигационных параметров не являются равноточными, т.е. их средние квадратические погрешности могут отличаться, что и происходит на практике, если измерения выполнены различными приборами или различными наблюдателями. Естественно, что вероятнейшая точка, полученная по МНК, должна быть ближе к той линии положения, которая точнее, а поэтому уравнивание измерений происходит с учетом их весов - величин, обратно пропорциональных квадратам среднеквадратических погрешностей измерений, которые формируют так называемую весовую матрицу. Методика вывода ничем не отличается от предложенной в п. 2.3.1.

Умножим слева правую и левую части уравнения (2.10) на матрицу W, которая имеет следующий вид:

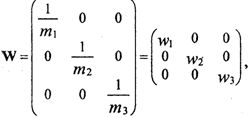
здесь т - средняя квадратическая погрешность измерения соответствующего нави­гационного параметра. Получим следующее уравнение:

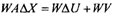
Теперь выражение (2.12) для Q перепишется так:

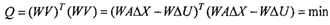
Используя изложенную ранее методику, получим систему нормальных уравнений с учетом неравноточных измерений, предварительно обозначив матрицу H^W-Kav. весовую матрицу D"¹:

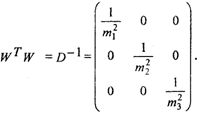
Система нормальных уравнений запишется:

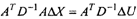
а решение будет иметь вид'

AX=(A^TD~^lA)~^\A^TD~ⁱAU

Если элементы матрицы (2.18) равны, это означает, что измерения равноточные и выражение (2.20) превращается в выражение (2.14). Формула (2.20) имеет более общий характер, чем уравнение (2.14).

Для определения координат опять воспользуемся формулой (2.8). Вероятнейшая точка, полученная по формуле (2.20), определяет средневзве­шенные значения координат.