Фазовые траектории нелинейных систем

В отличие от линейных систем в нелинейных системах, как указывалось выше, могут возникать незатухающие периодические движения, независящие от начальных условий, - автоколебания. На фазовой плоскости им соответствуют фазовые траектории, называемые предельными циклами.

Предельные циклы называются особымифазовымитраекториями. Различают следующие предельные циклы:

1). Устойчивый предельный цикл.

Реальные САР можно считать линейными чаще всего в предположении малости отклонений переменных от установившихся состояний. Если линейная система оказалась неустойчивой, то из-за фактической нелинейности в области больших отклонений, чем линеаризованная область, неустойчивая система как бы превращается в устойчивую (автоколебательную) нелинейную систему.

А и В — размеры предельного цикла.

2). Полуустойчивый предельный цикл.

а). Мягкий режим автоколебаний (система неустойчива в малом)

При сколько угодных малых отклонениях от состояния равновесия в системе возникают автоколебания.

б). Жесткий режим автоколебаний.

Точка попадает на предельный цикл лишь при больших отклонениях от состояния равновесия.

3). Неустойчивый предельный цикл.

В нелинейной системе может быть несколько предельных циклов. Из них некоторые могут быть устойчивы, а некоторые нет.

Здесь кроме особой точки 0 типа центра имеется два седла C₁ и C₁. Особые линии типа C₁A₂C₂ и C₂A₁C₁ называются сепаратрисами.

Здесь были рассмотрены нелинейные системы, которые при малых отклонениях можно принять линейными. Однако есть нелинейные системы, которые нельзя при малых отклонениях считать линейными (реле, характеристики с зоной нечувствительности (застоя), системы с сухим трением и т.д.).

Системам с зоной застоя состоянию равновесия соответствует не одна точка, а целая область возможных равновесных состояний.

Методы построения тазовых траекторий нелинейных систем

Аппарат фазовой плоскости позволяет производить исследование нелинейных систем достаточно просто, однако для построения фазового портрета следует иметь фазовые траектории. Фазовые траектории можно было бы построить определяя X₁ и X₂ по уравнению

,

однако для нелинейных систем интегрирование невозможно и приходится прибегать к другим методам, исключая интегрирование.

Метод изоклин

Изоклиной называется геометрическое место точек, где касательные к фазовым траекториям имеют одинаковый наклон.

Запишем уравнение системы 2-ого порядка:

;

;

;

;

;

— тангенс угла наклона фазовой траектории

Геометрическим местом точек, где тангенс угла наклона равен , будет:

.

Линии OC₁, OC₂,…, OC₈ — изоклины.

Если соединим строки, то получим фазовый портрет. Из любой начальной точки мы теперь можем перейти в следующую и т.д. Если начали в A₀ и пришли в A₀ — имеем цикл.

Пример.

;

;

;

;

;

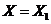— уравнение изоклины