Математическое описание нелинейных систем

Уравнение движения нелинейной системы в общем виде может быть представлено следующим выражением:

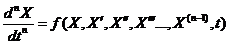(1)

где X — выходная величина.

Введем обозначения

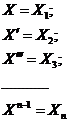
Заметим, что

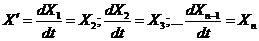
Тогда уравнение (1) примет вид:

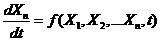
Зависимость правых частей уравнения от времени указывает, что заданы все необходимые возмущающие силы и управляющие воздействия. В этом случае система называется неавтономной. Если зависимость 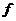от времени отсутствует, то заданная система называется автономной.

Понятие о фазовом пространстве

При качественном рассмотрении процессов в нелинейных системах удобно использовать геометрическое представление, основанное на понятии о фазовом пространстве (пространство в прямоугольной системе координат , которыми являются величины определяющие состояние системы.

Для системы n-го порядка фазовое пространство n-мерное.

Для системы 3-го порядка — 3-х мерное пространство, для системы 2-го порядка — 2-х мерная фазовая плоскость.

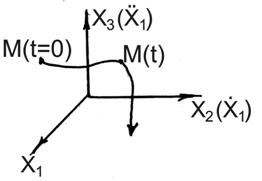
Состоянию системы в каждый момент времени соответствует точка в фазовом пространстве. Она называется изображающей. При изменении состояния системы изображающая точка движется в фазовом пространстве, описывая фазовую траекторию. Фазовая траектория дает полное представление о характере процесса в системе кроме временной оценки (время при построении фазовой траектории исключается).

В дальнейшем для простоты будем рассматривать систему 2-ого порядка (которым соответствует фазовая плоскость).

Уравнение нелинейной системы 2-ого порядка имеет вид:

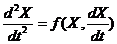(1)

Введя обозначения

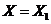; (2)

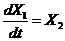, (3)

получим: 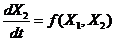. (4)

Разделив уравнение (3) на (4), получим уравнение фазовой траектории:

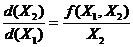. (5)

Свойства фазовых траекторий

1. Фазовые траектории направлены по часовой стрелке, т.е. если производная положительна, то X увеличивается.

2. Фазовая траектория пересекает ось абсцисс под прямым углом. Т.к. в данном случае , a , то .

Обозначим

тогда .

В состоянии равновесия

— угол наклона в данном случае неопределенный. Точки, соответствующие состоянию равновесия, называются особыми точками.

Сколько может быть состояний равновесия?

У линейных систем — одно, т.к. Р и Q — линейны, а две линии пересекаются в одной точке.

У нелинейных систем точек равновесия может быть несколько.

3. Через одну точку фазовой плоскости проходит только одна фазовая траектория (это утверждение основано на теореме Коши о единственности решения дифференциального уравнения).

Очень важным является суждение об устойчивости систем. Для линейных систем много критериев устойчивости. Когда выше мы говорили об устойчивости, то речь шла о единственном установившемся состоянии.

Для нелинейных систем существует несколько установившихся состояний (режимов), из которых некоторые устойчивые, некоторые неустойчивые. Здесь имеет смысл говорить лишь об устойчивости нелинейной системы в окрестности данного состояния равновесия.

Для нелинейных систем различают устойчивость: в малом, в большом, в целом.

Устойчивость в малом - это устойчивость при бесконечно малых отклонениях от исходного режима.

Устойчивость в большом — это устойчивость при конечных отклонениях, возможных в данной системе по условиям ее работы.

Устойчивость в целом — это устойчивость при неограниченных отклонениях.