Математическое описание дискретных систем

Решетчатые функции

Математическое описание импульсных АСУ усложняется из-за дискретного характера сигнала. Квантованный по времени сигнал может быть представлен выборкой ординат непрерывной функции времени (см. рис.1.1). Эти ординаты разделены периодом квантования, а внутри периодов все промежуточные значения равны нулю. Поэтому дискретный сигнал удобно описывать функциями дискретной переменной [6].

Рассмотрим функцию времени 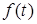, определенную для всех значений t и тождественно равную нулю для 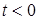(см. рис. 1.1).

Пусть n – натуральное число (n=0,12,3…) и Т – период дискретности. Функцией дискретного аргумента называетсячисловая последовательность f[0], f[T], f[2T],…, f[nT], получающаяся в результате выборки значений функции 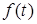в точках 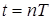, n – натуральное число. Для краткости ее называют решетчатой функциейи обозначают f[n].

При заданном интервале дискретности Т по функции 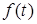решетчатая функция f[n] определяется однозначно. Непрерывная функция 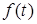– огибающая для своей решетчатой функции f[n]. Но поскольку через дискретные точки решетчатой функции можно провести множество огибающих, то обратного соответсвия между решетчатой функцией и “породившей” ее функцией 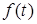нет: f[n]® .

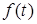Если необходимо определять значения функции между точками квантования, то вводят понятие смещенной решетчатой функции.

Смещенной решетчатой функциейназывается числовая последовательность – f[sT], f[T+sT],…, f[iT+sT],…, f[nT+sT], 0 £ s £ 1, образованная в результате выборки значений функций 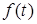в точках 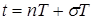оси времени, где s – постоянное число, лежащее в интервале 0 £s £ 1. Сокращенно f[n, s].

Поскольку значения решетчатой функции известны только для дискретных значений аргумента, то для изучения поведения таких функций методы дифференциального и интегрального исчисления оказываются непригодными.

Для оценки свойств решетчатой функции используется аппарат конечных разностей и конечных сумм, позволяющий оценивать свойства числовых последовательностей (функций дискретного аргумента).

Для исследования динамики дискретных импульсных АСУ используются разностные уравнения. Их решение, так же как и дифференциальных, представляет известные трудности. В связи с этим, в теории дискретных (импульсных) АСУ широко используются операционные методы.

Разностные уравнения

Если вместо переменной t ввести относительную переменную 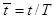, то непрерывной функции в относительном масштабе будет соответствовать решетчатая функция 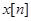. Она совпадает с 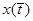при

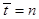
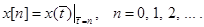(1.1)

Таким образом, решетчатая функция изменяет свое значение при целочисленных значениях независимого переменного n, а интервал между дискретами равен 1.

Дискретная функция не является однозначной, что видно из рис. 1.15.

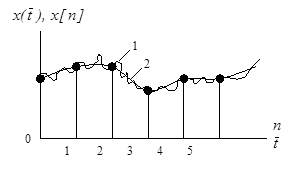
Рис. 1.15. Решетчатая функция

Для устранения этой неоднозначности вводят смещенные дискретные функции, позволяющие “просматривать” процессы внутри периодов Т.

Записывают смещенную функцию так

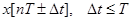. (1.2)

Однако на основе теоремы Котельникова можно сделать вывод, что если непрерывный сигнал 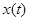не содержит гармоническую составляющую с частотой выше 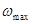, то при квантовании с периодом 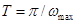дискретная решетчатая функция точно отобразит непрерывную функцию, т.е. потери информации при дискретизации не будет.

Для математического описания динамики дискретных систем применяют разностные уравнения. Они определяют связь между значениями решетчатой функции и, таким образом, форму огибающей данной решетчатой функции. Оценка связи значений решетчатой функции производится с помощью конечных разностей. Они являются аналогами производных в дифференциальных уравнениях.

Переход от дифференциальных уравнений к разностным основан на замене производных разностями соответствующих порядков (табл. 1.1).

Таблица 1.1

Соответствие производных и правых разностей

Порядок производной или разности	Непрерывная функция	Дискретная функция
.	. . .	. . .
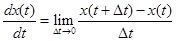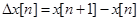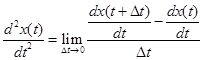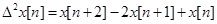m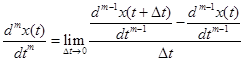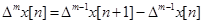

Первая разность решетчатой функции:

,

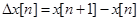и т.д.

То есть, для определения первой разности (рис. 1.16) надо знать два последовательных значения решетчатой функции.

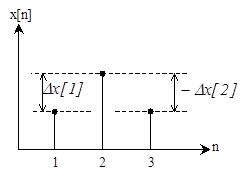
Рис. 1.16. К определению разностей решетчатой функции

Упомянутая выше аналогия между первой разностью и первой производной видна из того, что первая разность, как и первая производная, равна по существу, отношению приращения функции к приращению аргумента

,

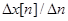но так как

,

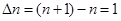то ее значение просто равно .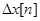

Вторая разность решетчатой функции:

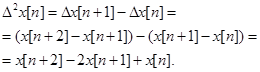
Для нахождения второй разности надо знать три последовательных значения решетчатой функции. Разность m-го порядка определяется выражением

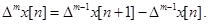
Рассмотрим простой пример дискретной функции и ее первой разности (рис. 1.17). Пусть 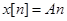. Ее первая разность 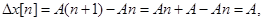т.е. является единичной ступенчатой дискретной функцией 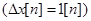. Вторая и высшие разности этой функции равны нулю.

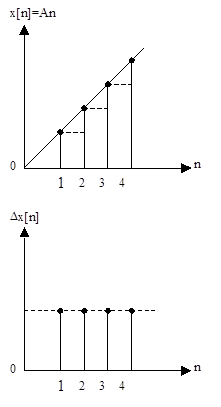
Рис. 1.17. Пример дискретной функции и ее первой разности

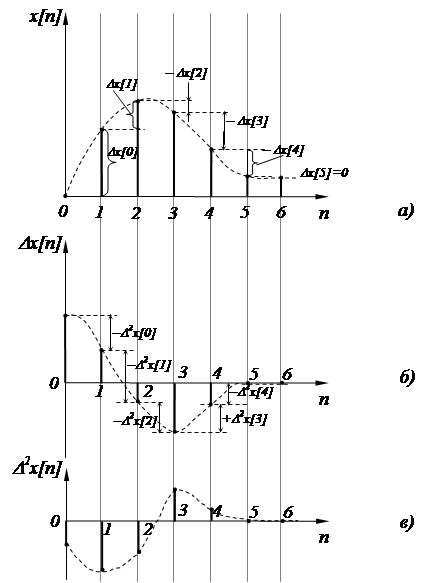
На рис. 1.18 в качестве примера приведена решетчатая функция произвольного вида x[n] (рис. 1.18, а), а также ее первая Dx[n] (рис. 1.18, б) и вторая D²x[n] (рис. 1.18, в) разности.

Разностное уравнение k-го порядка соответствует дифференциальному уравнению k-го порядка. Если линейное дифференциальное уравнение записывают в виде

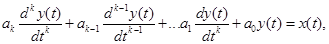(1.3)

то линейное разностное уравнение с постоянными коэффициентами можно записать так

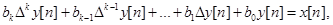(1.4)

где 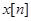– известная дискретная функция;

– искомая дискретная функция, получаемая в результате решения разностного уравнения.

Рис. 1.18. Решетчатая функция произвольного вида x[n],

а также ее первая Dx[n] и вторая D²x[n] разности

Дифференциальное уравнение можно рассматривать как предельное выражение для разностного уравнения при 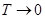. Решать разностные уравнения можно различными методами, аналогичными методам решения дифференциальных уравнений.

В теории управления часто применяют операционный метод решения дифференциальных уравнений, который позволяет свести решение к решению алгебраического уравнения.

Для решения разностных уравнений также используют операционный метод, основанный на дискретном преобразовании Лапласа, в частности Z-преобразовании.

1.2.3. Понятие о Z-преобразовании

Метод Z – преобразования нашел широкое применение при исследовании импульсных и цифровых систем управления [6]. Если поведение системы достаточно полно описывается только в дискретные моменты времени, то наиболее удобным математическим аппаратом для анализа и синтеза является аналог преобразования Лапласа – дискретное преобразование Лапласа или так называемое Z – преобразование.

Z – преобразованием решетчатой функции 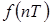называется функция комплексного аргумента Z, определяемая выражением

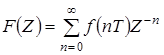. (1.5)

Это выражение может быть получено следующим образом. Если предыстория системы относительно 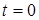учитывается соответствующими граничными условиями, то допустимо полагать, что непрерывная функция времени 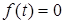при t<0. В этом случае, как известно, функция 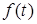может быть заменена изображением по Лапласу (одностороннее преобразование)

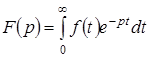. (1.6)

Выбрав конечный интервал времени равным периоду дискретности ( 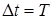) и представив текущее время в виде последовательности 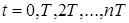, можно в выражении (1.6) интеграл заменить суммой, а величину dt периодом квантования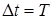

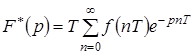. (1.7)

Выражение (1.7) представляет собой дискретное преобразование Лапласа. Предел этого выражения при 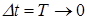дает преобразование Лапласа непрерывной величины (1.6).

Если обозначить 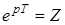, то

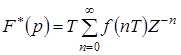. (1.8)

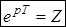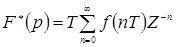Обозначив Þ , где 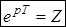– комплексное переменное.

При этом Z-преобразование, как следует из формулы (1.5), отличается от дискретного преобразования Лапласа только множителем Т, то есть

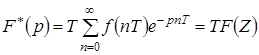. (1.9)

Итак, преобразование Лапласа для дискретной функции привело к бесконечной сумме. Бесконечная сумма является функцией комплексного переменного .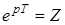

Операция суммирования носит название прямого дискретного преобразования Лапласа (или Z-преобразования) для решетчатой функции 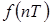в функцию комплексного переменного Z. Эта операция кратко обозначается, как 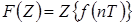и указывает, что 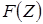есть Z – изображение решетчатой функции 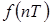или, короче, .

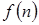Соответственно 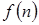является оригиналом 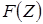. Изображение 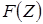существует, если (1.5) сходится. На основе выражения (1.5) получены таблицы Z-преобразований различных функций времени. В таблице 1.2 приведены выражения Z-преобразований для некоторых функций времени.

Таблица 1.2

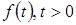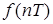		Изображение по Лапласу	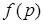Z-изображение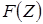
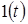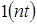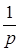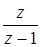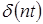t	nT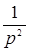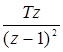

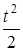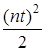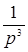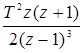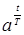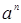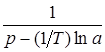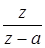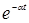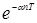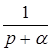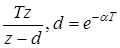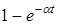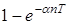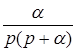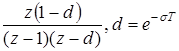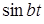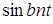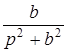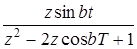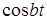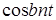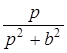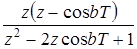Очевидно, что все функции времени, имеющие одинаковые значения в точках t=nT оси времени, обладают одинаковыми Z-преобразованиями 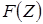. Это означает, что связь между функцией времени 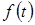и соответствующим ей Z-преобразованием 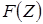не является взаимно однозначной. Функция 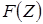характеризует только последовательность чисел 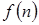, но не позволяет судить о поведении оригинала 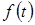внутри интервалов.

Модифицированное Z-преобразование.

Если значение Z-изображений необходимо знать не только в дискретные моменты времени t = nT, но и в любые другие моменты времени, смещенные на s по отношению к моментам квантования, то можно использовать модифицированное Z-преобразование

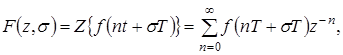(1.10)

где s – действительный независимый параметр, принимающий произвольное значение от нуля до единицы.

Модифицированное Z-изображение решетчатой функции либо определяется из формулы (1.10), либо следует использовать таблицы для модифицированного Z-преобразования.

Обратное Z-преобразование позволяет определить решетчатую функцию-оригинал 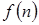или 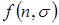по ее Z-преобразованию и сокращенно записывается в виде

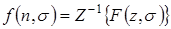или 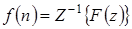. (1.11)

При заданной 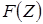существует три способа нахождения решетчатой функции: в виде бесконечного ряда, разложением на элементарные дроби и при помощи интеграла обратного преобразования.

Первый метод позволяет непосредственно получить числовую последовательность 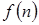. Если 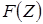представляет собой рациональную функцию, т.е. отношение двух многочленов, то, разделив многочлен числителя на многочлен знаменателя, получим бесконечный ряд Лорана. Числовые значения коэффициентов членов ряда определяют дискреты решетчатой функции 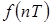. Указанный способ позволяет определять сколь угодно большое число значений n. При выполнении операции деления многочлены числителя и знаменателя следует записывать по возрастающим степеням ( ).

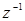Пример 1.

Дано: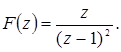

Определить: .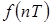

Решение: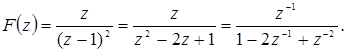

Путем непосредственного деления получим

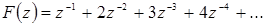
Отсюда

;

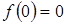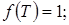
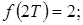
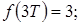
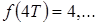
Второй метод основан на разложении функции 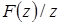на элементарные дроби и использовании таблицы преобразования. Непосредственно функция 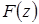на элементарные дроби не раскладывается, так как фигурирующие в таблице функции от z имеют в числителе множитель z.

Пример 2.

Дано: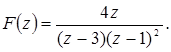

Определить: .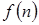

Решение: разложим 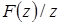на элементарные дроби

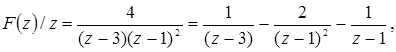
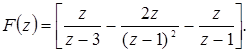
Из таблицы соответствия получим

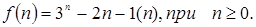
Третий метод нахождения решетчатой функции 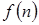основан на интеграле обратного преобразования

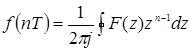
или

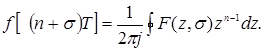
В этом случае интегрирование ведется по окружности 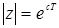, где с – абсцисса абсолютной сходимости. Окружность, по которой ведется интегрирование, охватывает все особые точки подынтегрального выражения. Формулы обратного преобразования мало применяются.

Использование аппарата Z-преобразования позволило развить теорию линейных дискретных АСУ, до некоторой степени аналогичную теории линейных систем непрерывного действия.

Рассмотрим модель импульсной АСУ (рис. 1.19).

В этой модели 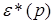– изображение сигнала 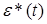в смысле дискретного преобразования Лапласа. Таким образом, передаточная функция импульсной АСУ Ф(р) является дискретно-непрерывной функцией р.

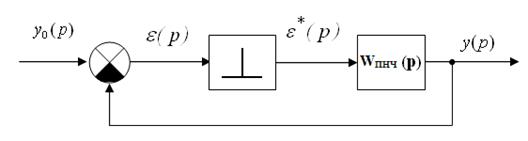
Рис. 1.19. Модель импульсной САУ

В непрерывных АСУ используют преобразование Лапласа вида

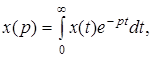(1.12)

где 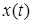– непрерывная функция (оригинал), 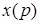– изображение.

Сигнал на выходе ПИЭ

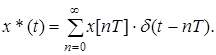(1.13)

Каждая ордината дискретной функции представляет собой 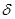-функцию, площадь которой определяется функцией 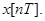В этом формальное различие между 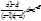и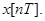

Изображение сигнала 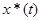в смысле дискретного преобразования Лапласа определяют по формуле

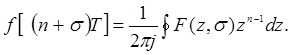(1.14)

где 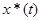– дискретная функция-оригинал, 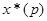– изображение.