Тема №16 «Корреляционно-регрессионный анализ»
Цель:научиться составлять выборочные уравнения линейной регрессии в случае сгруппированных данных, вычислять выборочный коэффициент линейной корреляции и проводить оценку его значимости, проверять значимость уравнения линейной регрессии с помощью дисперсионного анализа, делать прогноз значений зависимой переменной.
Краткие теоретические сведения:
Основная задача корреляционного анализа – выявление связи между случайными переменными и оценка её тесноты.
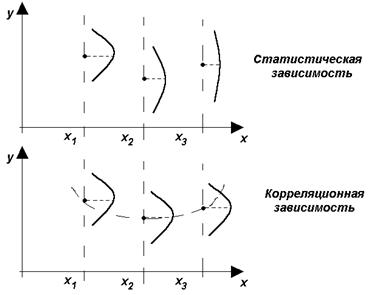
Статистической зависимостью называется зависимость, при которой изменение одной из величин влечёт изменение распределения других величин.
Частным случаем статистической зависимости является корреляционная зависимость, при которой изменение одной из величин изменяет среднее значение других.
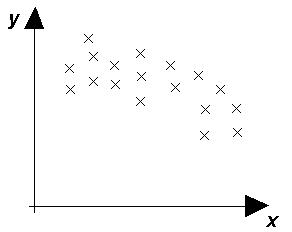
В психологических исследованиях имеет место статистический разброс данных: при одном и том же значении одной величины другая величина принимает несколько значений и наоборот. Графическое изображение экспериментальных данных называется диаграммой рассеяния.
Необходимы ответы на вопросы:
1) какой вид имеет тенденция,
2) какая теснота между тенденцией и разбросом данных.
Для этого необходимо не сгруппированные данные подвергаются первичной обработке. Составляется корреляционная таблица.
 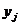 | 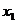 | 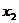 | … | 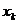 | 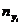 |
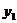 | 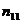 | 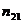 | … | 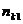 | 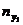 |
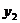 | 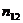 | 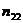 | … | 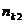 | 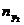 |
| … | … | … | … | … | … |
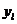 | 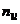 | 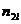 | … | 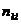 | 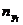 |
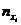 | 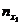 | 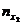 | … | 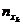 | 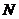 |
где  ,
, 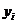 – середины интервалов,
– середины интервалов, 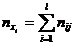 ,
, 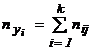 ,
, 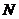
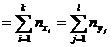 .
.
Для ответа на первый вопрос используем аппроксимацию. Наиболее простой вариант – квадратическая аппроксимация, которая обосновывает метод наименьших квадратов.
Суть его состоит в том, что сумма квадратов отклонений между экспериментальным и теоретическим значениями должна быть минимальной:
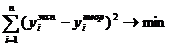 .
.
Если 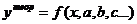 , тогда
, тогда 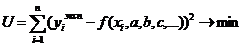 .
.
Из теории функции нескольких переменных известно, что для минимума необходимо равенство нулю всех частных производных:
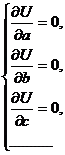
Решив данную систему относительно неизвестных коэффициентов 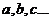 мы получим уравнения, которые называются уравнениями регрессии:
мы получим уравнения, которые называются уравнениями регрессии:
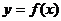 - выборочное уравнение регрессии
- выборочное уравнение регрессии 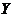 на
на 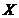 ,
,
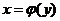 - выборочное уравнение регрессии
- выборочное уравнение регрессии 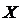 на
на 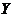 .
.
Для линейной зависимости:
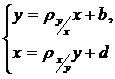
или
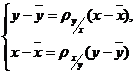 ,
,
где 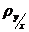 и
и 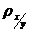 – выборочные коэффициенты регрессии
– выборочные коэффициенты регрессии 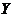 на
на 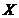 и
и 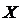 на
на 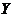 .
.
Для их нахождения используются формулы и данные корреляционной таблицы:
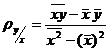 ,
, 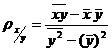 .
.
Для ответа на второй вопрос вводим еще одну характеристику, учитывающую разброс данных вокруг линии регрессии, то есть тесноту связи - выборочный коэффициент корреляции:
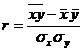
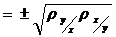
Знак ± берётся равным знаку коэффициентов регрессии, которые оба или положительны или отрицательны. При этом один коэффициент регрессии по абсолютной величине больше 1, другой - меньше 1. Коэффициент корреляции не имеет размерности и 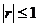 .
.
Так как выборка случайна, то отличное от нуля значение выборочного коэффициента линейной корреляции необходимо проверить на значимость.
1) на уровне a = 0,05 выдвигаем нулевую гипотезу 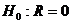 при конкурирующей
при конкурирующей 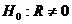 ,
,
2) в качестве критерия проверки используем случайную величину 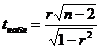 ,
,
3) табличное значение 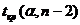 находим по таблице распределения Стьюдента,
находим по таблице распределения Стьюдента,
4) если 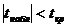 , то принимаем нулевую гипотезу, а значит, генеральный коэффициент линейной корреляции равен нулю.
, то принимаем нулевую гипотезу, а значит, генеральный коэффициент линейной корреляции равен нулю.
Основная задача регрессионного анализа – установление формы и изучение зависимости между переменными, оценка функции регрессии, прогноз значений зависимой переменной.
В регрессионном анализе рассматривается односторонняя зависимость случайной зависимой переменной 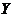 от одной (или нескольких) неслучайной независимой переменной
от одной (или нескольких) неслучайной независимой переменной  :
: 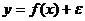 , где
, где 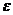 - возмущение, характеризующее отклонение от функции регрессии.
- возмущение, характеризующее отклонение от функции регрессии.
Будем рассматривать только линейный регрессионный анализ.
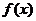 определяется по МНК, а воздействие неучтённых случайных факторов и ошибок наблюдений в модели находится с помощью дисперсии возмущений или остаточной дисперсии, несмещённой оценкой этой дисперсии является выборочная остаточная дисперсия:
определяется по МНК, а воздействие неучтённых случайных факторов и ошибок наблюдений в модели находится с помощью дисперсии возмущений или остаточной дисперсии, несмещённой оценкой этой дисперсии является выборочная остаточная дисперсия:
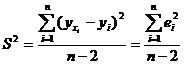 ,
,
где 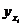 – групповая средняя, найденная по уравнению регрессии,
– групповая средняя, найденная по уравнению регрессии, 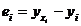 – выборочная оценка возмущения или остаток регрессии.
– выборочная оценка возмущения или остаток регрессии.
Доверительный интервал прогноза среднего значения:
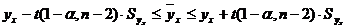 ,
,
где
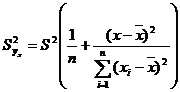 ,
,
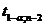 находим по таблице распределения Стьюдента
находим по таблице распределения Стьюдента
При определении доверительного интервала для индивидуальных значений 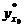 зависимой переменной вместо
зависимой переменной вместо 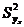 берём
берём
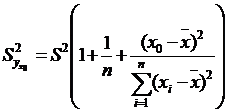 .
.
Доверительный интервал для прогнозов индивидуальных значений 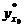 определяется формулой:
определяется формулой:
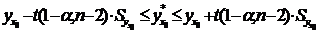 .
.
Проверка значимости уравнения регрессии (используется дисперсионный анализ):
Вычисляем несмещённые оценки дисперсий зависимой переменной, обусловленных соответственно регрессией и воздействием неучтённых случайных факторов и ошибок, 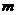 - число оцениваемых параметров уравнения регрессии,
- число оцениваемых параметров уравнения регрессии, 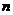 - число наблюдений по формулам:
- число наблюдений по формулам:
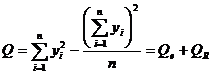 ,
,
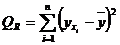 ,
, 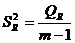 ,
,
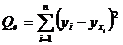 ,
, 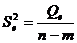 .
.
Гипотеза о значимости уравнения регрессии принимается, если
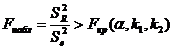 , где
, где 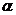 уровень значимости,
уровень значимости, 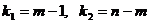 и отвергается, если
и отвергается, если 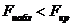 .
.
Контрольные вопросы:
1. Статистическая и корреляционная зависимость.
2. Диаграмма рассеяния.
3. Корреляционная таблица.
4. Расчет средних по данным корреляционной таблицы.
5. Суть метода наименьших квадратов.
6. Выборочные коэффициенты линейной регрессии, их свойства и геометрический смысл.
7. Выборочные уравнения линейной регрессии.
8. Выборочный коэффициент линейной корреляции и его свойства.
9. Проверка гипотезы о значимости выборочного коэффициента линейной регрессии.
10. Основная задача регрессионного анализа.
11. Основные предпосылки регрессионного анализа.
12. Возмущения и дисперсия возмущений.
13. Доверительный интервал прогноза среднего значения.
14. Доверительный интервал прогноза индивидуального значения.
15. Проверка значимости уравнения регрессии.
Контрольные задания:
1. При исследовании пяти групп людей на степень подверженности гипнозу использовались различные методики. Получены следующие данные:
 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
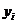 | 1,0 | 1,3 | 1,4 | 1,9 | 2,0 |
Проверить целесообразность линейной аппроксимации зависимости результатов исследований от конкретной методики и определить коэффициенты этой зависимости МНК.
2. Используя метод наименьших квадратов, сгладить с помощью функций заданного вида следующие табличные зависимости:
а) 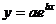
| x | -1 | ||||
| y |
б) 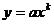
| x | ||||||
| y |
в) 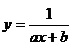
| x | -2 | -1 | ||||
| y | 0,8 | 0,4 | 0,1 |
3. Составить выборочные уравнения линейной регрессии Y на Х и Х на Y, вычислить выборочный коэффициент корреляции по выборочным данным, представленным в таблице:
 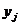 | |||||||
4. При обследовании 50 учеников 4-го класса получены следующие данные о весе и росте учащихся:
(24,125) (28,128) (26,128) (30,133) (25,127) (26,127) (27,127) (28,130)
(26,127) (27,128) (27,128) (28,129) (28,130) (24,126) (28,130) (29,131)
(26,127) (28,131) (26,128) (29,130) (27,130) (29,130) (27,129) (26,127)
(28,129) (28,130) (25,128) (28,129) (29,131) (27,130) (27,129) (29,131)
(28,129) (27,128) (25,126) (27,129) (28,129) (27,129) (29,129) (27,128)
(28,129) (28,130) (26,128) (25,126) (30,132) (25,127) (26,129) (26,129)
(27,128) (29,132)
Представить результаты обследования в виде корреляционной таблицы. По данным корреляционной таблицы оценить тесноту связи между весом (X) и ростом (Y) учеников четвертого класса и составить выборочное уравнение линейной регрессии X на Y.
5. Проверить значимость выборочных коэффициентов корреляции, полученных в задачах 2 и 3 при 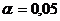 .
.
Задания для домашней работы:
1. Используя метод наименьших квадратов, сгладить с помощью функций заданного вида следующие табличные зависимости:
а) 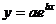
| x | 1,8 | 2,4 | 2,7 | 3,3 | |
| y |
б) 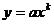
| x | 0,5 | ||||
| y |
в) 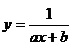
| x | -2 | 1,2 | 1,5 | ||
| y | 0,3 | 0,2 | 0,2 | 0,2 |
2. При приёме на работу 14 кандидатам на вакантные должности было предложено два теста. Результаты тестирования (в баллах) приведены в таблице:
 | ||||||||||||||
 |
а) найти уравнение регрессии 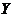 по
по  ,
,
б) проверить значимость уравнения регрессии на 5%-ном уровне по 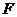 - критерию,
- критерию,
в) оценить среднее значение показателя второго теста с показателем первого 60 баллов и построить для него 95%-ный интервал, аналогичный доверительный интервал найти для индивидуальных значений.
