Тема №9 «Основные законы распределения случайных величин»

Цель:познакомиться с основными законами распределения дискретных и непрерывных случайных величин, научиться применять их при решении задач теории вероятностей прикладного характера.

Краткие теоретические сведения:

Случайная величина Х имеет биномиальное распределение с параметрами n и p, где и 0<p<1, если , k=0,1,…,n.

, .

Случайная величина имеет распределение Пуассона с параметром , если она принимает целые неотрицательные значения с вероятностями, которые определяются по формуле , k=0,1,…

, .

Случайная величина имеет геометрическое распределение с параметром р (0<p<1), если она может принимать только натуральные значения с вероятностями , .

, .

Случайная величина имеет гипергеометрическое распределение с параметрами m и n, , если она принимает целые неотрицательные значения с вероятностями .

, .

Случайная величина имеет равномерное распределение на отрезке , если её распределение задаётся плотностью .

Функция равномерного распределения .

, .

Случайная величина имеет показательное распределение с параметром , если её распределение задаётся плотностью .

Функция показательного распределения .

, .

Cлучайная величина имеет нормальный закон распределения (закон Гаусса) с параметрам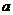и и 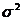, если ее плотность вероятности имеет вид:

Кривую нормального закона распределения называют нормальной или Гауссовой кривой.

Математическое ожидание случайной величины , распределенной по нормальному закону, равно параметру 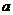этого закона, то есть , а ее дисперсия – параметру 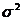, то есть .

Функция распределения нормальной случайной величины , выражается через функцию Лапласа по формуле:

.

Свойства случайной величины, распределенной по нормальному закону:

1) Вероятность попадания случайной величины , распределенной по нормальному закону, в интервал (х₁;х₂), равна

,

где ,

2) Вероятность того, что отклонение случайной величины , распределенной по нормальному закону, от математического ожидания 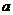не превысит величину, равна

, где .

Правило «трех сигм»:

Если случайная величина имеет нормальный закон распределения с параметрам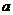и и 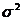, то есть , то достоверно, что ее значения заключены в интервале .

Нормальный закон распределения случайной величины с параметрами , , то есть называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что X примет значение, принадлежащее интервалу (10;50).

Решение. х₁=10, х₂=50, σ =1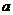0, =30.

P(10<Х<50)= =2Ф(2).

Из таблицы находим Ф(2)=0,4772 и окончательно имеем

P(10<Х<50)=2·0,4772=0,9544.

Контрольные вопросы:

1. Биномиальное распределение, его характеристики.

2. Распределение Пуассона, его характеристики.

3. Геометрическое распределение, его характеристики.

4. Гипергеометрическое распределение, его характеристики.

5. Равномерное распределение, его характеристики.

6. Показательное распределение, его характеристики.

7. Нормальный закон распределения случайной величины.

8. Изменение гауссовой кривой при изменении параметров σ и .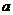

9. Функция распределения и плотность вероятности нормальной случайной величины.

10. Вероятность попадания нормально распределённой случайной величины в заданной интервал.

11. Вероятность отклонения нормально распределённой случайной величины от её математического ожидания.

12. Правило «трёх сигм».

Контрольные задания:

1. На большой перемене между занятиями в двух случаях из 10 вы покупаете булочку и кофе. Найти вероятность того, что в течение 5 дней в большую перемену вы будете питаться именно так.

2. В «Службу доверия» города Энска поступает в среднем 3 обращения в час. Какова вероятность того, что за 2 часа будет:

а) 5 обращений,

б) от 4 до 7 обращений,

в) не более 3 обращений.

3. Пусть в опытах по психодиагностике вероятность того, что тестируемый субъект зафиксирует световую вспышку в указанном секторе, равна 0,8. Какова вероятность того, что вспышка будет впервые обнаружена в третьем опыте?

4. Каждый день с 15.00 до 15.30 вы стоите у книжного киоска и ожидаете свою незнакомку, которая каждый раз проходит мимо не ранее 15.20, не замечая вас. Каково среднее время её появления в период вашего ожидания?

5. Психоаналитик на работе никогда не скучал, так как посетители шли к нему «валом». Если вы тоже захотите навестить знаменитого специалиста, рассчитайте вероятность обслуживания вас в ближайшие полчаса с учётом того, что поток обслуженных клиентов имеет плотность 4 человека в час. Каково среднее время обслуживания?

6. Математическое ожидание и дисперсия нормально распределённой случайной величины равны соответственно 12 и 3. Записать функцию и плотность распределения данной случайной величины.

7. Математическое ожидание порога чувствительности в серии психофизических опытов равно 40, а дисперсия – 100. Вычислить вероятность того, что в данном испытании порог будет заключен в интервале (30; 80), считая распределение порога нормальным.

8. Пусть случайная величина Х – центрированная. σ(Х)=5. Вычислить вероятность того, что величина Х не превосходит по абсолютной величине значения 5.

9. Математическое ожидание и СКО уровня настойчивости Х, распределённого по нормальному закону, соответственно равны 40 и 0,4. Какое значение данного показателя можно гарантировать с вероятностью 0,8?

Задания для домашней работы:

1. В группе 30 студентов, среди них 10 отличников. В деканат вызваны наугад 8 студентов. Какова вероятность, что среди вызванных ровно 3 отличника?

2. Производится взвешивание на аналитических весах, причём имеются гирьки весом не менее 1 г. Найти математическое ожидание ошибки и её дисперсию.

3. Уровень тревожности в нормальной обстановке распределён по показательному закону: . Найти вероятность того, что в результате испытаний уровень тревожности попадёт в интервал (0,2; 0,5).

4. Известно, что для человека pH крови является случайной величиной, имеющей нормальное распределение с математическим ожиданием и средним квадратическим отклонением . Найти вероятность того, что уровень pH находится между 7,35 и 7,45.