Введение в математический анализ
101-110. Найти пределы функции, не пользуясь правилом Лопиталя.
101. а) 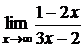 ; б)
; б) 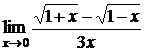 ;
;
в) 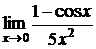 ; г)
; г) 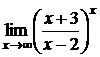 .
.
102. а) 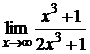 ; б)
; б) 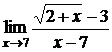 ;
;
в) 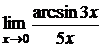 ; г)
; г) 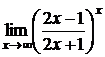 .
.
103. а) 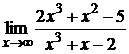 ; б);
; б); 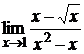
в) 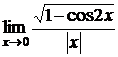 ; г)
; г) 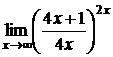 .
.
104. а) 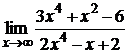 ; б)
; б) 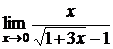 ;
;
в) 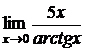 ; г)
; г) 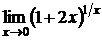 .
.
105. а) 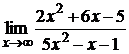 ; б)
; б) 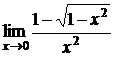 ;
;
в) 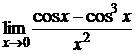 ; г)
; г) 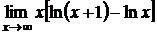 .
.
106. а) 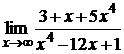 ; б)
; б) 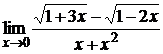 ;
;
в) 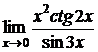 ; г)
; г) 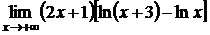 .
.
107. а) 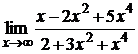 ; б)
; б) 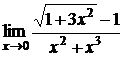 ;
;
в) 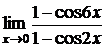 ; г)
; г) 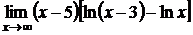 .
.
108. а) 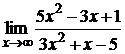 ; б)
; б) 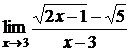 ;
;
в) 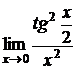 ; г)
; г) 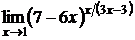 .
.
109. а) 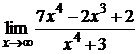 ; б)
; б) 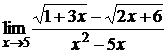 ;
;
в) 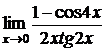 ; г)
; г) 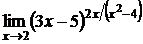 .
.
110. а) 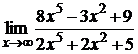 ; б)
; б) 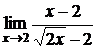 ;
;
в) 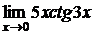 ; г)
; г) 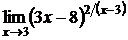 .
.
ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ
111-120. Исследовать функцию с помощью производной и построить ее график.
111. f(x) = 3x2 + 8x – 2. 116. f(x) = 2x – x2 + 3.
112. f(x) = 6x3 – 5x + 7. 117. f(x) = 4x3 – 7x + 2.
113. f(x) = 2x2 + x + 1. 118. f(x) = x2 + 6x – 7.
114. f(x) = 2x2 – 3x + 8. 119. f(x) = x2 – 3x + 1.
115. f(x) = 4x – x2. 120. f(x) = 8x2 + 2x – 7.
121-130. Задана функция y = f(x) и два значения аргумента x1 и x2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого значения аргумента; 2) в случае разрыва функции найти ее пределы в точке слева и справа; 3) сделать схематический чертеж.
121. f(x) = 91/(2 – x), х1 = 0, х2 = 2.
122. f(x) = 41/(3 – x), х1 = 1, х2 = 3.
123. f(x) = 121/x, х1 = 0, х2 = 2.
124. f(x) = 31/(4 – x), х1 = 2, х2 = 4.
125. f(x) = 81/(5 – x), х1 = 3, х2 = 5.
126. f(x) = 101/(7 – x), х1 = 5, х2 = 7.
127. f(x) = 141/(6 – x), х1 = 4, х2 = 6.
128. f(x) = 151/(8 – x), х1 = 6, х2 = 8.
129. f(x) = 111/(4 + x), х1 = -4, х2 = -2.
130. f(x) = 131/(5 + x), х1 = -5, х2 = -3.
131-140. Найти производные 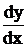 данных функций.
данных функций.
131. а) 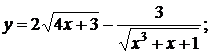 б)
б) 
в) 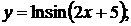 г)
г) 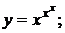 д)
д) 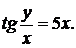
132. а) 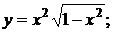 б)
б) 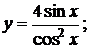 в)
в) 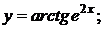
г) 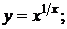 д)
д) 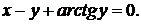
133. а) 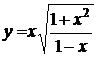 ; б)
; б) 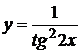 ; в)
; в) 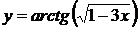
г) 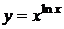 ; д) y sin x = cos (x – y)
; д) y sin x = cos (x – y)
134. а) 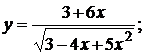 б)
б) 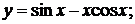 в)
в) 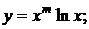
г) 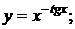 д)
д) 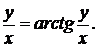
135. а) 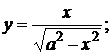 б)
б) 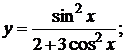 в)
в) 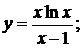
г) 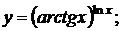 д)
д) 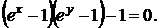
136. а) 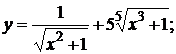 б)
б) 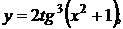 в)
в) 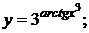
г) 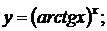 д)
д) 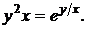
137. а) 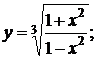 б)
б) 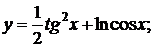 в)
в) 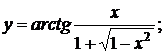
г) 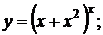 д)
д) 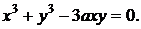
138. а) 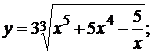 б)
б) 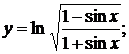 в)
в) 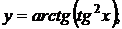
г)  д)
д) 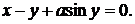
139. а) 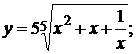 б)
б) 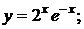 в)
в) 
г) 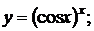 д)
д) 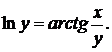
140. а) 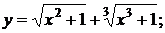 б)
б) 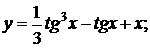
в) 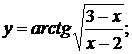 г)
г) 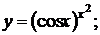 д)
д) 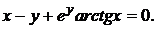
141-150. Найти производные 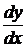 и
и 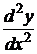 для заданных функций: а) y = f(x); б) y = y(t), x = j(t).
для заданных функций: а) y = f(x); б) y = y(t), x = j(t).
141. а) 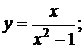 б)
б) 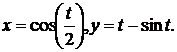
142. а) 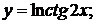 б)
б) 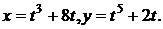
143. а) 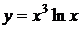 ; б) x = t – sint, y = 1 – cost.
; б) x = t – sint, y = 1 – cost.
144. а) 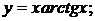 б)
б) 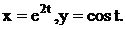
145. а) 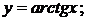 б)
б) 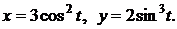
146. а) 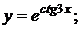 б)
б) 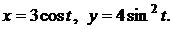
147. а) 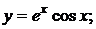 б)
б) 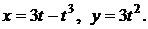
148. а) 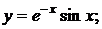 б)
б) 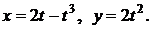
149. а) 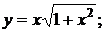 б)
б) 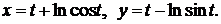
150. а) 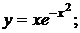 б)
б) 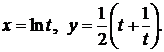
151-160. Найти полный дифференциал функции.
151. а) 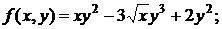 б)
б) 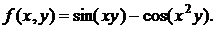
152. а) 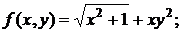 б)
б) 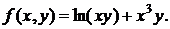
153. а) 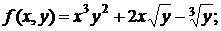 б)
б) 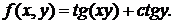
154. а)  б)
б) 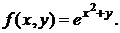
155. а) 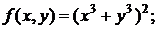 б)
б) 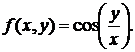
156. а)  б)
б) 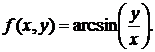
157. а) 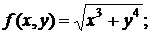 б)
б) 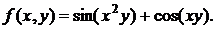
158. а) 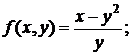 б)
б) 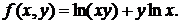
159. а) 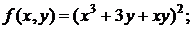 б)
б) 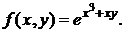
160. а) 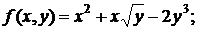 б)
б) 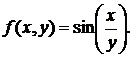
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
161-170. Найти неопределенный интеграл методом подстановки.
161. 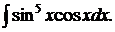 166.
166. 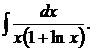
162. 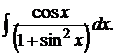 167.
167. 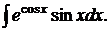
163. 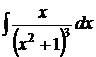 . 168.
. 168. 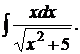
164. 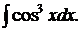 169.
169. 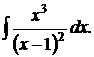
165. 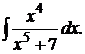 170.
170. 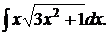
171-180. Методом интегрирования по частям найти интеграл.
171. 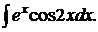 176.
176. 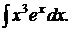
172. 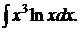 177.
177. 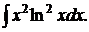
173. 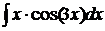 . 178.
. 178. 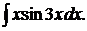
174. 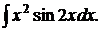 179.
179. 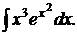
175. 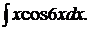 180.
180. 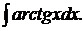
ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
181-190. Определить площадь фигуры, ограниченной линиями:
181. y = (x – 3)2, y = 9.
182. y = 3(1 – x2), y = 5/3.
183. y = x2 + 9, y = х + 9.
184. y = 2(x2 + 3), y = 8.
185. y = (x + 4)2, y = 8.
186. y = 4 – x2, y = 1.
187. y = 2(x2 + 1), y = 4.
188. y = 3(1 – x2), y = 2.
189. y = 2(1 – x2), y = 1.
190. y = (x – 4)2, y = 8.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
191-200. Найти общее решение дифференциального уравнения первого порядка.
191. а) (x + y)dx + xdy = 0; б) y' + 3y = e2x.
192. а) (x2 + y2)dx + xydy = 0; б) 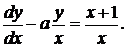
193. а) (xyey/x + x2)dy – y2ey/xdx= 0; б) x(1 – x2)dy + (2x2 – 1)dx = x2dx
194. а) (x – y)dx + (x + y)dy = 0; б) y' – ay = ebx.
195. а) x3y' = y(y2 + x2); б) y' – yctgx = ctgx.
196. а) (x – ycos(y/x))dx + xcos(y/x)dy = 0; б) x2y' – 2xy = 3.
197. а) x2 – y2 + 2xyy' = 0; б) ydy – xdx = 4dx.
198. а) xy + y2 = (2x2 + xy)y'; б) y' = 1/x + 2x2.
199. а) (x2 – yx2)y' + y2 + xy2 = 0; б) (x + 3)dy = 2ydx.
200. а) y' = ex – y; б) y' =ex + 3e-x.
201-210. Найти общее решение линейного дифференциального уравнения второго порядка.
201. y" + 3y' – 4y = 0;
202. y" – 2y' – 5y = 0;
203. y" – 9y = 0;
204. y" – y = 0;
205. 4y" – 12y' + 9y = 0;
206. y" + 2 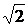 y' + 2y = 0;
y' + 2y = 0;
207. y" – 2y' + 50y = 0;
208. y" – 4y' + 7y = 0;
209. y" + 25y = 0;
210. y" + 6y' = 0;
Контрольная работа № 2
СЛУЧАЙНЫЕ СОБЫТИЯ
211-220. Найти вероятность появления события.
211. а) Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди 5-ти случайно выбранных волокон смеси обнаружить менее 2-х окрашенных?
б) Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.
212. а) Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из 6-ти посеянных семян взойдут не менее 5-ти?
б) Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,8. Найти вероятность того, что из 2-х проверенных изделий только одно стандартно.
213. а) Два равносильных противника играют в шахматы. Что вероятнее выиграть: не менее 2-х партий из 4-х или не менее 3-х партий из 5-ти?
б) Вероятность того, что в течение одной смены возникнет неполадка станка, равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за три смены?
214. а) Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди 5-ти взятых наугад изделий: 1) нет ни одного испорченного; 2) будет 2 испорченных.
б) В ящике имеется 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
215. а) Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель 2-х пуль и более, если число выстрелов равно 5000.
б) Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
216. а) Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): 3 партии из 4-х или 5 из 8-ми?
б) В первой урне содержится 10 шаров, из них 8 белых; во второй урне содержится 20 шаров, из них 4 белых. Из каждой урны наудачу извлекают по одному шару, а затем из этих двух шаров наугад взят один шар. Найти вероятность того, что взят белый шар.
217. а) Найти вероятность того, что событие А появится не менее 3-х раз в 4-х независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.
б) Устройство содержит 2 независимо работающих элемента. Вероятность отказа элементов равна соответственно 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один из элементов.
218. а) Событие В появится в случае, если событие А наступит не менее 4-х раз. Найти вероятность наступления события В, если будет произведено 5 независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.
б) Имеется два одинаковых ящика с шарами. В первом ящике находится 2 белых и 1 черный шар, во втором - 3 белых и 4 черных шара. Наудачу выбирают один ящик и вынимают из него шар. Какова вероятность того, что вынутый шар окажется белым?
219. а) Монету бросают 5 раз. Найти вероятность того, что герб выпадет: 1) менее 2-х раз; 2) не менее 2-х раз.
б) В ящике 10 красных и 8 синих пуговиц. Вынимают наудачу 2 пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
220. а) Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность того, что в течение часа позвонят 5 абонентов?
б) В читальном зале имеется 6 учебников по теории вероятности, из которых 3 в переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
221-230. Случайная величина Х задана функцией распределения F(x). Найти: а) плотность вероятности f(x); б) вероятность попадания величины Х в заданный интервал; в) математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины Х.
221. 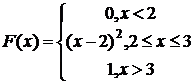 (1; 2,5)
(1; 2,5)
222. 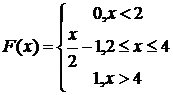 (2; 3)
(2; 3)
223. 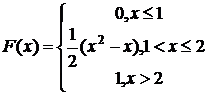 (1; 1,5)
(1; 1,5)
224. 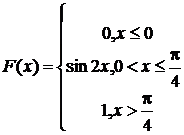 (p/6; p/4)
(p/6; p/4)
225. 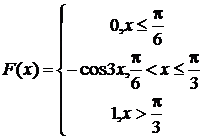 (p/6; p/4)
(p/6; p/4)
226. 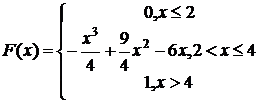 (3; 4)
(3; 4)
227. 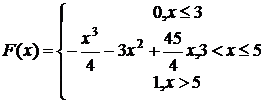 (3,5; 4)
(3,5; 4)
228. 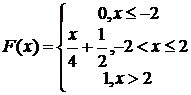 (0; 1)
(0; 1)
229. 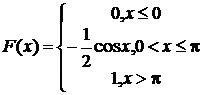 (p/6; p/2)
(p/6; p/2)
230. 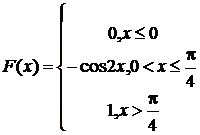 (p/6; p/4)
(p/6; p/4)
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
231-240. В итоге измерений некоторой физической величины Х одним из прибором (без систематических погрешностей) получены результаты, приведенные в таблице. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов; в) абсолютную и относительную погрешности при доверительной вероятности g = 0,95.
| 231. | 6,7 | 6,5 | 6,7 | 6,4 | 6,9 | 7,0 | 7,2 | 6,7 | 6,5 | 7,2 |
| 7,0 | 7,1 | 6,8 | 6,9 | 6,5 | 6,4 | 6,6 | 6,3 | 6,4 | 6,5 |
| 232. | 8,4 | 8,9 | 8,9 | 8,6 | 9,0 | 8,5 | 9,3 | 8,3 | 8,9 | 8,6 |
| 8,5 | 8,4 | 8,7 | 8,9 | 8,6 | 9,0 | 8,2 | 8,6 | 8,9 | 8,7 |
| 233. | 7,9 | 7,6 | 8,0 | 7,6 | 7,4 | 7,6 | 7,8 | 8,0 | 7,7 | 8,0 |
| 7,8 | 7,7 | 7,9 | 7,5 | 7,6 | 7,8 | 8,1 | 7,6 | 7,7 | 7,6 |
| 234. | 4,3 | 4,5 | 4,7 | 4,9 | 4,5 | 4,6 | 4,8 | 4,3 | 4,7 | 4,2 |
| 4,8 | 4,9 | 5,0 | 4,7 | 4,6 | 4,4 | 4,3 | 4,6 | 4,8 | 4,7 |
| 235. | 3,4 | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 3,8 | 3,9 | 3,4 |
| 3,7 | 3,8 | 3,5 | 4,0 | 4,1 | 4,2 | 3,7 | 3,3 | 3,5 | 3,6 |
| 236. | 2,3 | 2,7 | 2,5 | 2,3 | 2,4 | 2,5 | 2,8 | 2,7 | 2,3 | 2,4 |
| 2,6 | 2,9 | 2,7 | 2,5 | 2,8 | 3,0 | 3,1 | 2,8 | 2,9 | 2,7 |
| 237. | 1,8 | 1,9 | 1,5 | 1,6 | 1,8 | 1,7 | 1,4 | 1,6 | 1,5 | 1,7 |
| 1,9 | 2,0 | 2,1 | 1,8 | 1,6 | 1,7 | 1,5 | 1,7 | 1,8 | 1,9 |
| 238. | 9,4 | 9,6 | 9,7 | 9,4 | 9,3 | 9,6 | 9,8 | 9,9 | 10,0 | 10,1 |
| 9,8 | 9,7 | 10,2 | 9,6 | 9,7 | 9,8 | 9,7 | 9,8 | 9,9 | 10,0 |
| 239. | 11,4 | 11,2 | 11,3 | 11,6 | 11,4 | 11,3 | 11,7 | 11,6 | 11,8 | 11,7 |
| 11,8 | 11,9 | 11,6 | 11,7 | 11,5 | 11,4 | 11,2 | 11,3 | 11,1 | 11,1 |
| 240. | 15,2 | 15,1 | 15,3 | 15,4 | 15,7 | 15,6 | 15,5 | 15,4 | 15,6 | 15,7 |
| 15,6 | 15,8 | 15,5 | 15,7 | 15,9 | 16,0 | 15,8 | 15,6 | 15,5 | 15,9 |
