Линейная регрессия, корреляция

Статистическая зависимость величины Y от величины X - это такая зависимость, при которой каждому значению величины X из множества ее возможных значений соответствует некоторое множество возможных значений величины Y, характеризуемое определенным законом распределения. Частным случаем статистической зависимости является корреляционная зависимость между величинами, когда изменение одной из величин влечет изменение математического ожидания другой.

Корреляционную зависимость Y от X можно описать с помощью уравнения вида: M(Y)_x = f(x), (4.16)

где M(Y)_x – условное математическое ожидание величины Y, соответствующее данному значению x; f(x) – некоторая функция.

Уравнение вида (4.16) называется уравнением регрессии Y на X.

Если функция f(x) линейная, то уравнение регрессии можно записать в виде: M(Y)_x = Ax + B, (4.17)

где A и B – параметры.

Первым этапом статистической обработки результатов с целью определения наличия и вида корреляционной зависимости между изучаемыми величинами является построение корреляционной таблицы (табл. 4.1): в первой строке таблицы указываются все встречающиеся в выборке значения величины X – x₁, x₂, ¼, x_i (i = 1, ¼, k); в первом столбце указываются все встречающиеся в выборке значения величины Y – y₁, y₂, ¼, y_j (j = 1, ¼, l); на пересечении строк и столбцов указываются частоты n_ij, равные числу появлений пары (x_i; y_j) в выборке; в последней строке указываются числа n_xi, равные количеству появления в выборке значения x_i, и n_yj, равные количеству появления в выборке значения y_j.

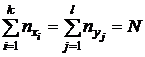(N – объем выборки). Корреляционная таблица содержит всю информацию, полученную в результате выборочных наблюдений.

Таблица 4.1.

yj xi	x1	x2	¼	xk	ny
y1	n11	n21	¼	nk1	ny1
y2	n12	n22	¼	nk2	ny2
¼	¼	¼	¼	¼	¼
yl	n1l	n2l	¼	nkl	nyl
nx	nx1	nx2	¼	nxk	N

С помощью корреляционной таблицы для каждого значения x_i можно записать соответствующее распределение величины Y.

В случаях, когда существует линейная зависимость между величинами X и Y, для описания корреляционной зависимости вводятся выборочные уравнения линейной регрессии: 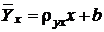, (4.18)

где r_yx – выборочный коэффициент регрессии, имеющий смысл выборочной оценки коэффициента А (см. формулу 4.17), условное среднее 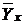является оценкой условного математического ожидания M(Y)_x, а параметр b – оценкой B.

Для нахождения выборочных коэффициентов регрессии применяется метод наименьших квадратов (МНК), суть которого заключаются в следующем. Пусть результаты выборочных наблюдений представлены в виде совокупности точек, указывающей на приблизительно линейный характер зависимости Y от X. Необходимо найти такие параметры уравнения регрессии, при которых соответствующая прямая линия представляла бы эту совокупность точек наилучшим образом. В качестве критерия оптимальности принимают требование, что сумма квадратов отклонений ординат всех эмпирических точек от ординат соответствующей прямой должна быть минимальна, т.е.:

сумма 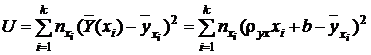(4.19)

должна быть минимальна.

Из условия минимума этой функции следует, что ее частные производные ¶U/¶r и ¶U/¶b должны обращаться в нуль, т.е.:

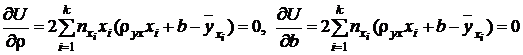
В результате получаются уравнения для определения интересующих нас параметров:

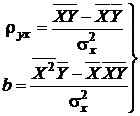, (4.20)

где

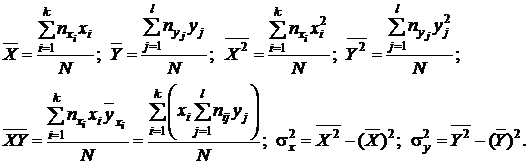(4.21)

Пример 4.4. Составить уравнение линейной регрессии Y на X для корреляционной связи между массой таблетки и скоростью ее растворения по данным, приведенным в таблице.

Х Y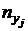
		–	–	–	–
1,5			–	–	–
	–			–	–
2,5	–	–	–		–
	–	–		–
3,5	–	–	–
						N=10

Решение. 1) Уравнение регрессии Y на X: 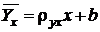, где r_yx – выборочный коэффициент регрессии, b – выборочная оценка. 2) На основании данных, приведенных в таблице, найдем условные средние 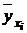величины Y для всех значений X:

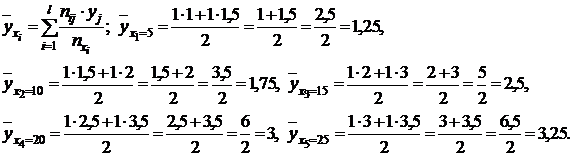
3) Найдем условные средние 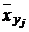величины X для всех значений Y:

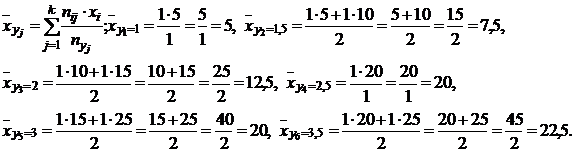
4) Составим вспомогательные расчетные таблицы для нахождения коэффициентов регрессии:

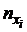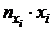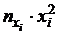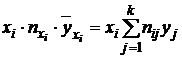	2×5 = 10	2×52 = 50	5×2,5 = 12,5
	2×10 = 20	2×102 = 200	10×3,5 = 35
	2×15 = 30	2×152 = 450	15×5 = 75
	2×20 = 40	2×202 = 800	20×6 = 120
	2×25 = 50	2×252 = 1250	25×6,5 = 162,5
S=10	S=150	S=2750	S=405

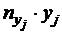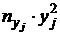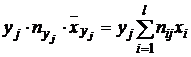	1×1 = 1	1×12 = 1	1×5 = 5
	2×1,5 = 3	2×1,52 = 4,5	1,5×15 = 22,5
	2×2 = 4	2×22 = 8	2×25 = 50
	1×2,5 = 2,5	1×2,52 = 6,25	2,5×20 = 50
	2×3 = 6	2×32 = 18	3×40 = 120
	2×3,5 = 7	2×3,52 = 24,5	3,5×45 = 157,5
S=10	S=23,5	S=62,25	S=405

5) Найдем дополнительные величины (согласно формулам 4.21):

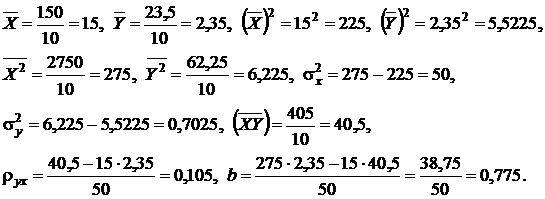
6) Составим уравнение регрессии Y на X: .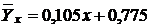

Для полного описания корреляционной связи недостаточно найти форму корреляционной зависимости между величинами, необходимо еще определить силу этой зависимости по величине коэффициентов регрессии. Для количественной характеристики силы (тесноты) связи вводится понятие выборочного коэффициента линейной корреляции, определяемого отношением:

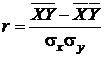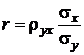, или , или 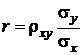. (4.22)

Пример 4.5. Пользуясь данными примера 4.4, найти выборочный коэффициент корреляции между массой таблетки и скоростью ее растворения.

Решение: воспользовавшись формулой (4.22), найдем коэффициент r:

.
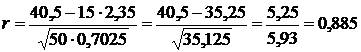