ЛПЗ 1. Парная линейная регрессия и корреляция

Условие. Имеются выборочные данные по совокупности крупных и средних организаций об урожайности зерновых культур и затратах на минеральные удобрения (файл MS EXCEL «Исходные данные», лист – номер вашей группы, номер варианта (первый столбец) – ваш номер в журнале преподавателя, каждый вариант – это выборка из 20 хозяйств). Исходные данные, используемые в данном примере, приведены в таблице 1.1.

Требуется:

1. Обосновать и оценить параметры парной модели линейной регрессии, решив систему нормальных уравнений (1.7).

2. Самостоятельно вывести формулы (1.8 и 1.9) из 1.7 и рассчитать коэффициенты регрессии.

3. Рассчитать коэффициент полной регрессии как средневзвешенную величину.

4. Рассчитать коэффициент парной линейной корреляции как средневзвешенную величину. Сделать выводы.

Методические указания.

1. В регрессионном анализе изучается направленная, односторонняя зависимость переменной y от одной (парная регрессия) или нескольких (множественная регрессия) независимых переменных х. Поскольку учесть влияние всех факторов на формирование зависимой переменной невозможно, то уравнение регрессии f(x) не может полностью объяснить каждое отдельное значение y:

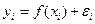, 1.1

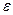– это отклонение от линии регрессия (остаток), случайная величина, отражающая влияние всех неучтенных факторов:

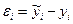. 1.2

Если f(x) – линейная функция, то получим регрессионную модель:

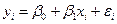, 1.3

поскольку в регрессионном анализе изучается усредненная по y зависимость, а остатки, являясь случайной величиной («белым шумом»), имеют нормальное распределение и в среднем равны нулю (взаимопогашаются):

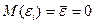, 1.4

то главной задачей парного линейного регрессионного анализа является оценка параметров уравнения:

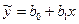. 1.5

Как правило, регрессионные модели в статистике строятся по выборочным данным, выборочное уравнениерегрессии 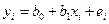является оценкой генерального уравнения. Параметры уравнения 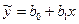могут быть оценены методом наименьших квадратов, условием которого является минимизация остаточного объема вариации:

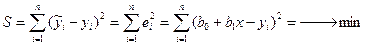. 1.6

Экстремум, как известно, достигается в точке, где производная функции равна нулю, поэтому для оценки параметров находят частные производные функции 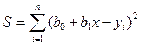по искомым параметрам и приравнивают их к нулю:

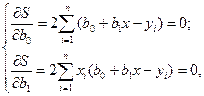1.7

после преобразования, учитывая, что постоянную величину можно вынести за знак суммы и то, что суммирование постоянной величины можно заменить ее умножением на число единиц совокупности, получим систему нормальных уравнений:

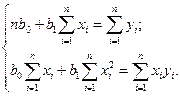1.8

По имеющимся данным может быть построена модель зависимости урожайности зерновых, как показателя характеризующего уровень и эффективность производства зерна, от уровня его интенсивности, важным показателем которого, особенно в современных условиях развития сельского хозяйства России, является уровень внесения минеральный удобрений. Учитывая причинно-следственные связи, примем за у урожайность зерновых, а за х – затраты на минеральные удобрения в расчете на 1 га посевной площади. Тогда модель регрессии будет иметь вид: .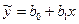

На основе решения системы уравнений 1.8 по выборочным данным (табл. 1) было получено уравнение:

.

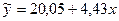2. На основе решения системы уравнений могут быть получены формулы (предлагается вывести самостоятельно) для оценки параметров:

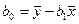, 1.9

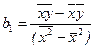. 1.10

В числителе коэффициента полной регрессии 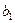получен показатель, называемый ковариацией:

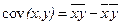, 1.11

в знаменателе – аналог ковариации одной переменной – дисперсия переменной х: 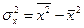. 1.12

На основе формул 1.8 и 1.9 получены те же результаты:

;

.

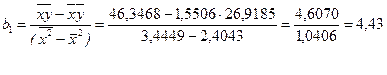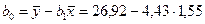3. Если подставить выражение (1.9) в модель (1.5), то получим: 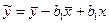, после преобразования:

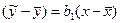, 1.13

откуда следует интерпретация коэффициента полной регрессии b₁ как коэффициента пропорциональности. Он показывает, на сколько единиц в среднем изменится зависимая величина y, если независимая величина х изменится на единицу, т.е. 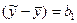, если .

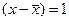Из выражения (1.13) следует, что линия регрессии пройдет через точку 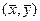, т.е. 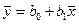, если записать это уравнение в форме отклонения от средних, то получим 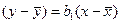, для каждого отдельного наблюдения можно вычислить коэффициент 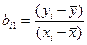, для совокупности в целом коэффициент полной регрессии рассчитывается как средняя взвешенная:

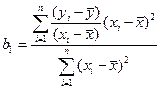. 1.14

В качестве признака-веса выбирается квадрат отклонений независимой переменной от средней, поскольку с учетом свойств средней величины .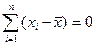

Выражение (1.14) показывает, что коэффициент полной регрессии по

форме построения действительно средняя величина, которая является величиной именованной.

Рассчитаем коэффициент полной регрессии как средневзвешенную величину, результаты расчетов оформим в таблицу 1.1.

Средние значения переменных: , 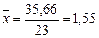; среднеквадратические отклонения: , .

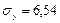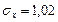Коэффициент полной регрессии равен:

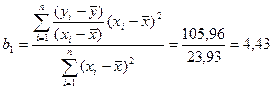ц/га,

Таблица 1.1