Площадь поверхности вращения.

Пусть кривая АВ задана ур-нием , и пусть ф-я неотриц. и непрерывна вместе со своей производной на , тогда поверхность вращения, образованная вращением кривой АВ вокруг оси Ох имеет площадь, к-рая выражается ф-лой:

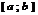Объём тела вращения.Рассм. нек-рое тело и вычтем его объем. Допустим, что известны площади сечений этого тела плоскостями перпендикулярными оси Ох. С изменением х, меняются площади сечений, т.е. площади сечений явл. нек-рой ф-ей от х. Тогда , где непрерывна на . В частности если тело образовано вращением части кривой , , тогда площадь сеч.: , тогда

17)Понятие первообразной. Неопределённый интеграл и его свойства. Таблица основных интегралов. Понятие об основных методах интегрирования (замена переменной, интегрирование по частям).

Понятие о первообразной функции.

определенная на интервале АВ, наз-тся первообразной данной функции f(x) в этом промежутке, если для любого Є(a,b)

F(x) =sin x, F(x) =ln x,

f(x) =cosx; f(x) = .

Теорема: если f(x) - первообр., то множ-во также явл. первообр.

Неопределенный интеграл и его св-ва.

О.Если ф-я F(x)-первообразная ф-и f(x), то множ-во всех первообр. наз-ют неопределенным интегралом от f(x) и обозначают

f(x)- подинтегральная ф-я, f(x) dx – подинтегральное выражение; операция нахождения неопр. интеграла наз-тсяинтегрированием.

Св-ва:

1.Производная неопр. интеграла = подинтегральнойф-и. Дифференциал от неопр. интеграла = подинтегральному выражению.

2.Неопр. интеграл от дифференциала нек-рой ф-и = этой ф-и с точностью до постоянной.

3.Постоянный множитель можно выносить за знак интеграла.

,

4.Если ф-и f(x) и g(x) имеют первообр., то ф-я f(x)+ g(x) также имеет первообр.Причём

Таблица неопр. интегралов:

;

Понятие об основных методах интегрирования.

I. М-д непосредственного интегрирования.

Пример:

II. М-д замены переменной.

Теорема: если F(x)-первообр. f(x), -дифференц. ф-я. Тогда также имеет первообр. Причем

Док-во: По правилам диф. сложной ф-и дает , т.е. -одна из первообр. для . След-но .

Поскольку совпадает с , тогда

Пример:

III. М-д интегрирования по частям основан на след.форме:

Пример:

Интегрирование простейших рациональных дробей.

Пример: разложить рац-но дробь в сумму простейших дробей

м-д неопр. коэф-тов

Интегрирование тригонометрических ф-ий.

Вычисление интеграла вида , , ,

сводится к вычислению интегралов от рац. ф-ий, роль переменной играет t. если R(sinxcosx) явл. нечетной относительно sinx, то вводят замену cosx= t. Если R(sinxcosx) явл. нечетной относ-но cosx, то вводят замену sinx= t. Если ф-я R (sinxcosx)явл. нечетной относ-но sinx и cosx, то вводят замену tgx=t.

Интегрирование иррац. ф-и

Интегралы типа

вычисляются путем полного квадрата под радикалом и дальнейшей заменой