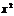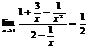Бесконечно большие и бесконечно малые ф-и.
О. Ф-я 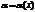 наз-тся бесконечно малой при
наз-тся бесконечно малой при 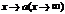 , если
, если 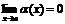 ;
; 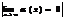 . Н.:
. Н.: 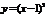 явл. бесконечно малой при
явл. бесконечно малой при 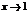 .
.
Св-ва бесконечно малых ф-ий:
1. если ф-я 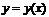 имеет предел
имеет предел 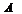 при
при 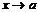 , то
, то 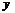 можно принять
можно принять 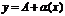 , где
, где 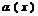 – бесконечно малая при
– бесконечно малая при 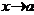
2. если ф-я 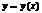 представляется в виде
представляется в виде 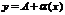 , где
, где 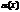 –бесконечно малая при
–бесконечно малая при 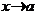 , то предел
, то предел 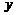 при
при 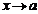 будет равен
будет равен 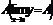
3. сумма конечного числа бесконечно малых ф-ий при 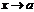 будет бесконечно малой ф-ей при
будет бесконечно малой ф-ей при 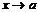
4. произведение двух бесконечно малых ф-ийпри 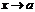 есть бесконечно малая при
есть бесконечно малая при 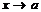 .
.
5. произведение бесконечно малой ф-и при 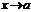 на ограниченную ф-ю есть бесконечно малая ф-я, при
на ограниченную ф-ю есть бесконечно малая ф-я, при 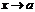
6. произведение бесконечно малой ф-и при 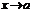 на постоянную есть бесконечно малая при
на постоянную есть бесконечно малая при 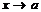 .
.
О.Ф-я 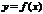 наз-тся бесконечно большой при
наз-тся бесконечно большой при 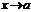 , если
, если 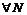 >0 можно найти такое число d>0, что при "
>0 можно найти такое число d>0, что при "  0<
0< 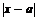 <dÞ
<dÞ 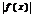 >
> 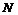 .
.
Бесконечно большая ф-я при 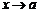 не имеет предела. Условно говорят, что
не имеет предела. Условно говорят, что 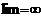 и пишут
и пишут 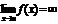 .
.
10)Основные теоремы о пределах ф-ии.
Замечательные пределы.
Т. Ф-я не может иметь более 1-го предела при 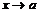 .
.
Док-во:
Предположим,что для 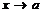 ,существует 2 предела,тогда А1-А2+о1(х)+о2(х)=0,где о1(х) и о2(х)-бесконечно малые,тогда А1=А2;
,существует 2 предела,тогда А1-А2+о1(х)+о2(х)=0,где о1(х) и о2(х)-бесконечно малые,тогда А1=А2;
Т. Если каждая из ф-ий 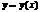 и
и 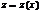 имеет предел при
имеет предел при 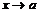 , то их сумма, разность, произведение также имеют пределы. Причем предел при
, то их сумма, разность, произведение также имеют пределы. Причем предел при 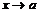
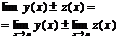
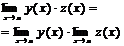
Если кроме того 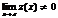 , то сущ-ет предел частного причем предел частного равен частному пределов.
, то сущ-ет предел частного причем предел частного равен частному пределов.
Док-во:
Докажем для произведения пусть предел у(х) при х стремящемся к а равен А,а предел z(x) при х стремящемся к а равен В.По свойствам бесконечно малых функций у(х)=А+о(х),а z(x)=В+р(х),где о(х)и р(х)-бесконечно малые при х стремящемся к а..Рассмотримпроизведение:предел при х стремящемся к а(у(х)*z(x))=пределу при х стремящемся к а((А+о(х))*(В+р(х)))=пределу при х стемящемся к а АВ+бесконесномалая(бм)+бм+бм
Следствие 1. Постоянный множитель можно выносить за знак предела, т.е. 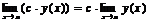
Следствие 2. Если 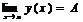 , то
, то 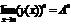
Т. Пусть ф-и 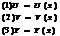 определены в нек-рой окрестности точки
определены в нек-рой окрестности точки  . Если для
. Если для 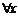 из этой окрестности вып-тсянер-во
из этой окрестности вып-тсянер-во 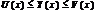 и ф-и (1), (2) имеют одинак. пределы при
и ф-и (1), (2) имеют одинак. пределы при 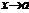 , то ф. (3) имеет тот же предел при
, то ф. (3) имеет тот же предел при 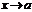 .
.
Док-во:
Пусть предел функции при х стремящемся к а U(x)= пределу функции при х стремящемся к а V(х),т.к. 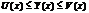 ,тоU(х)-А
,тоU(х)-А  У(х)
У(х)  V(x),по определению предела для любого эпсилан больше 0 существует дельта 1 и дельта 2 больше нуля,такие что /х-а/
V(x),по определению предела для любого эпсилан больше 0 существует дельта 1 и дельта 2 больше нуля,такие что /х-а/  дельта1 следовательно /U(x)-A/
дельта1 следовательно /U(x)-A/  эпсилан;/х-а/
эпсилан;/х-а/  дельта2 следовательно /V(x)-A/
дельта2 следовательно /V(x)-A/  эпсилан
эпсилан
Положим дельта=минимальной(дельта1+дельта2),тогда/х-а/  дельта,следовательно/У(х)-А/
дельта,следовательно/У(х)-А/  Эпсилан..А это по определению означает,,что предел при х стремящемся к а У(х)=А
Эпсилан..А это по определению означает,,что предел при х стремящемся к а У(х)=А
Т. Пусть ф. 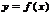 определена в нек-ром промежутке, содержащем
определена в нек-ром промежутке, содержащем 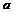 и если при
и если при 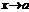 ф-я имеет «+»(«-«) предел, то найдется такая окрестность точки
ф-я имеет «+»(«-«) предел, то найдется такая окрестность точки 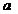 , что для
, что для 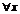 из этой окрестности ф.- «+» («-«).
из этой окрестности ф.- «+» («-«).
Док-во:
если функция имеет предел /f(x)-a/  эпсилан;а-эпсилан
эпсилан;а-эпсилан  f(x)
f(x)  a+эпсилан..положим эпсилан=а/2;существует дельта больше 0;а/2
a+эпсилан..положим эпсилан=а/2;существует дельта больше 0;а/2  f(x)
f(x)  3a/2,т.к. а больше 0,то f(x) больше 0,
3a/2,т.к. а больше 0,то f(x) больше 0,
Т. Если ф. 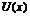 и
и 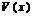 определены в нек-ром промежутке, содержащем точку
определены в нек-ром промежутке, содержащем точку  и для
и для 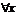 из этого промежутка кроме
из этого промежутка кроме 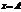 вып-тсянер-во
вып-тсянер-во 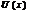 <
< 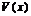 причем ф.
причем ф. 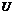 и М имеют пределы при
и М имеют пределы при 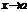 , тогда
, тогда 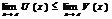 .
.
Док-во:
Пусть предел при х стремящемся к а U(x)=А,и предел при х стремящемся к а V(x)=В;предположим,что А больше В,по теореме сохранения знака предел при х стремящемся к а (U(x)-V(x))=А-В.Значит найдется такая окресность точки А в которой U(x)-V(x)  0,что противоречит условию следовательно условие не верно и А
0,что противоречит условию следовательно условие не верно и А  В
В
О. Отношение двух ф. 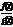 есть неопределенность вида
есть неопределенность вида 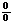 (или
(или 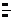 ) если
) если 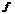 и
и 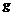 бескон. малые (беск. большие). В этом случае о пределе частного нельзя ничего определенного сказать, он может быть =0, = постоянной или =¥. Раскрыть эти неопределенности значит вычислить предел если он сущ-ет или док-ть, что он не сущ-ет.
бескон. малые (беск. большие). В этом случае о пределе частного нельзя ничего определенного сказать, он может быть =0, = постоянной или =¥. Раскрыть эти неопределенности значит вычислить предел если он сущ-ет или док-ть, что он не сущ-ет.
1-метод раскрытия неопределенности-сокращение общего множителя.
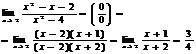
2-метод: деление на степень  .
.
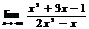 разделим на
разделим на